Soluzioni

CORSO DI LAUREA IN SCIENZE BIOLOGICHE
Appello di FISICA, 17 gennaio 2011
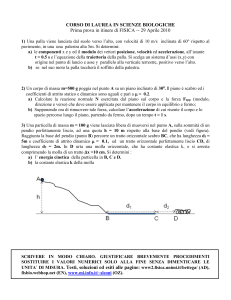
1) Una particella di massa m = 1 kg viene lasciata libera di muoversi dalla sommità (A) di un piano
inclinato. L’altezza AH del piano è pari a h = 6 m e l’angolo di inclinazione del piano è  30 °.
Si determini:
a) il lavoro compiuto dalla forza peso e quello della
reazione normale al piano d’appoggio durante lo
A
spostamento della particella da A fino a B , alla base
del piano inclinato.
C
B
b) dopo aver raggiunto il punto B , la particella
prosegue il suo moto lungo un piano scabro
H
(coefficiente di attrito  =0.3). Calcolare a quale
distanza BC, dalla base del piano inclinato, si arresta.
2) Due lamine metalliche infinitamente estese sono uniformemente cariche con densità di carica
superficiale di segno opposto e modulo  = 1.77  10-7 C/m2. La distanza d tra le lamine è 10 cm. Un
elettrone (di massa me) si stacca, con velocità iniziale nulla, dalla
lamina carica negativamente.
Determinare:
a) il campo elettrico fra le due lamine metalliche e la forza agente
sull’elettrone. Per entrambi si precisino modulo, direzione e verso.
b) la velocità dell’elettrone nell’istante in cui raggiunge la lamina positiva.
[ Note:
si trascuri la forza di gravità
e = 1.6 10-19 C
me = 9.11 10-31 kg
0 = 8.85 10-12 C2/Nm2
3) Un corpo di forma irregolare e di volume V = 30 cm3 ha al suo interno una cavità vuota di volume V0 = V/3.
Il materiale di cui è costituito il corpo ha densità o doppia rispetto a quella dell’acqua. Il corpo viene immerso
completamente in acqua. Determinare:
a) la spinta di Archimede di cui risente il corpo, specificandone direzione e verso;
b) la forza Fapp che è necessario applicare affinché il corpo all’equilibrio sia completamente immerso
in acqua (specificare direzione e verso di Fapp).
4) Due moli di un gas perfetto biatomico passano dallo stato iniziale A a quello finale D, attraverso le
trasformazioni reversibili AB (isoterma) , BC (isobarica ), CD (isovolumica), dove
pA= 2 104 N/ m2, pB= 0.5 pA , VC= VA= 1 m3, pD= 0.25 pA.
a) si disegnino nel piano ( V, p) le trasformazioni AB, BC e CD e si determinino le coordinate
termodinamiche (p,V,T) dei punti A, B, C, D
b) si calcoli il lavoro totale compiuto dal gas durante le trasformazioni da A fino a D e la
corrispondente variazione totale di energia interna .
[ Nota: R= 8.31 J/Kmole ]
SCRIVERE IN MODO CHIARO. GIUSTIFICARE BREVEMENTE I PROCEDIMENTI. SOSTITUIRE I
VALORI NUMERICI SOLO ALLA FINE. NON SCORDARE LE UNITA` DI MISURA. Testi, soluzioni ed esiti
alle pagine: www2.fisica.unimi.it/bettega/ (AD), qinf.fisica.unimi.it (EN), www.mi.infn.it/~sleoni (OZ)
SOLUZIONE ESERCIZIO 1
a) Il lavoro compiuto dalla forza peso e quello compiuto dalla reazione normale al piano durante
lo spostamento della particella da A fino a B sono rispettivamente :
dove P// è la componente della forza Peso parallela ad AB e d è la lunghezza
LPeso = P// d
di AB
LNormale = N// d dove N// è la componente della forza Normale parallela ad AB
Indicata con h l’altezza AH del piano inclinato , si ha :
P// = P sen30° = mg sen30° ; d = h / sen30 e pertanto LPeso = mg h = 58.8 J.
(Piu’ rapidamente il lavoro della forza Peso può essere calcolato come differenza dei valori
dell’energia potenziale associata al campo della forza Peso in A e in B , U(A)-U(B) , che vale
mgh-0 = mgh) .
N// = 0 e pertanto LNormale = 0
b) Quando raggiunge il punto B la particella ha energia meccanica E(B) uguale a quella che aveva
nel punto A , E(A). Inoltre E(B) è tutta energia cinetica, Ecin (B), in quanto U(B) =0).
Nel tratto BC compie lavoro (LBC ) solo la forza di attrito particella – piano, pertanto il lavoro
compiuto dalla forza risultante agente sulla particella che si sposta da B a C è LBC = -mg (BC).
Per il teorema lavoro – energia cinetica LBC= Ecin (C) - Ecin (B) = 0 – E(A) = - mgh
Si ha quindi -mg (BC) = - mgh da cui (BC) = h/  = 20 m
SOLUZIONE ESERCIZIO 2
a) Le due piastre piane cariche producono al loro interno un campo


1.77 10 7 C / m 2 
 
E i 
i  (20 10 3 N / C ) i
2
2
12
0
8.85 10 C / Nm
ossia perpendicolare alle due piastre e con verso dalla piastra positiva a quella negativa.
La forza elettrica subita dall’elettrone è pari a



1.77  10 7 C / m 2 
 
14
Fe  qE   eE  (  e)(  )i  (1.6  10 19 C )
i


N
i
(
0
.
32
10
)
0
8.85  10 12 C 2 / Nm 2
ossia è diretta lungo x con verso concorde all’asse.
b) L’ accelerazione subita dall’elettrone è unicamente dovute alla forza elettrostatica, originata dal
campo elettrico:



Fe  m e a e   eE
ossia:



eE (1.6  10 19 C )( 20  10 3 N / C ) 
ae  

i  (3.52  10 15 m / s 2 )i
 31
me
9.1  10 kg
Essendo l’accelerazione costante, il moto all’interno delle due piastre è rettilineo uniformemente
accelerato, per cui il legame fra velocità e posizione (quando l’elettrone urta l’armatura) è dato da:
v 2e  v 02e  2a e ( x f  x i )  0  2a e d  2a e d
ve 
2a e d 
2(3.52  10 15 m / s 2 )(0.1m )  2.65  10 7 m / s
SOLUZIONE ESERCIZIO 3
a) La spinta di Archimede è la forza, diretta verticalmente verso l’alto, che agisce su un corpo immerso in
un fluido. L’intensità di tale forza è pari al peso del fluido spostato dal corpo. Nel caso in esame:
FA  m f g
  H 2 0Vg
m
kg
 30(10  2 m) 3  9.8 2
3
m
s
 0.294 N  0.3 N
 10 3
b) All’equilibrio, la somma vettoriale delle forze agenti sul corpo è pari a zero.




Ftot  Fapp  Fg  FA  0
Proiettiamo ora l’equazione precedente sull’asse y verticale, supponendo Fapp concorde in verso con l’asse y:
Fapp  Fg  FA  0
Fapp  Fg  FA
Fapp  mc g  m f g
 ( mc  m f ) g
 (  c (V  V0 )   f V ) g
V


 2  f (V  )   f V  g
3


4
 (  1)  f Vg
3
 f Vg

3
1
kg
m
  10 3 3  30  10 6 m 3  9.8 2
3
m
s
2
 9.8  10 N
Il segno della forza applicata è risultato positivo, quindi il verso è concorde con quello del semiasse positivo y
(come la spinta Archimedea) .
SOLUZIONE ESERCIZIO 4
a)
p
A
C
B
D
V
pA = 2 10 4 N/ m2 VA = 1 m3 TA = pA VA / n R = 1203.4 K
pB = 0.5 pA = 10 4 N/ m2 VB = 2 VA = 2 m3 TB = 1203.4 K
pC = pB = 0.5 pA = 10 4 N/ m2 VC = VA = 1 m3 TC = pC VC / n R =0.5 pA VA / n R = 601.7 K
pD = 0.25 pA = 0.5 10 4 N/ m2 VD = VC = VA = 1 m3 TD = pD VD / n R =0.25 pA VA / n R = 300.8 K
b) Ltot = LAB + LBC + LCD
LAB = nR TA ln (VB / VA ) = 13860 J
LCD = 0 J Ltot = 3860 J
∆E = n cV (TD - TA) = - 37500 J
LBC = pC (VC - VB ) = - 10000 J