Conservatività della forza peso
Vogliamo dimostrare che la forza peso è una forza conservativa.
Sappiamo che una forza è conservativa se il lavoro da essa esercitato su una qualunque linea chiusa
è nullo.
Analizziamo, quindi, il caso di un bambino che sale su uno scivolo tramite una scala verticale, si
lascia scivolare lungo il piano inclinato e ritorna al punto di partenza per una nuova salita.
Verificheremo che il lavoro fatto dalla sua forza peso su tutto il percorso è uguale a zero.1
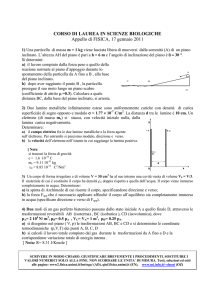
Il percorso del bambino può essere scomposto nei tre tratti: AB, BC e CA2 e di conseguenza il
lavoro complessivo sarà dato dalla somma dei tre lavori parziali:
LA-A = LA-B + LBC + LCA
Nel primo tratto AB (v. fig.) il vettore peso P3 e il vettore spostamento S hanno verso opposto e
quindi formano un angolo α di 180°; in questo tratto il modulo dello spostamento è h, quindi:
LA-B = P ⋅ S = mg h cos 180° = − mgh
Nel secondo tratto, agisce la componente Ps della forza peso tangente al piano inclinato. Sempre
con riferimento alla figura 1 si ha:
Ps = Psenβ
In questo tratto, lungo l, Ps e S sono concordi, quindi α = 0° e cos 0° = 1:
LBC = P ⋅ S = Ps l cos 0° = Psenβl = mg senβl
1
Notiamo innanzitutto che la forza peso P = mg è costante, quindi la nostra “dimostrazione” si può applicare ad ogni
altra forza costante.
2
Notiamo che la nostra non si può considerare una vera dimostrazione, perché dovremmo provare che il lavoro è nullo
su qualunque percorso chiuso; si tratta comunque di una convincente verifica.
3
Non potendo rappresentare la linea sopra la lettera per indicare un vettore si userà il grassetto mentre il carattere
normale indicherà il suo modulo
Essendo β l’inclinazione dello scivolo, si ha
l = h / senβ, quindi
LBC = mg senβ h / senβ = mgh
Nel tratto finale P e S formano un angolo di 90° ed essendo cos 90° = 0, il lavoro è nullo.
Sommando i tre contributi si ha dunque:
LA-A = LA-B + LBC + LCA = − mgh + mgh + 0 = 0