CORSO DI LAUREA IN SCIENZE BIOLOGICHE
Prima prova in itinere di FISICA -- 29 Aprile 2010
1) Una palla viene lanciata dal suolo verso l’alto, con velocità di 10 m/s inclinata di 60° rispetto al
pavimento, in una una palestra alta 5m. Si determini:
a) le componenti x e y ed il modulo dei vettori posizione, velocità ed accelerazione, all’istante
t = 0.5 s e l’equazione della traiettoria della palla. Si scelga un sistema d’assi (x,y) con
origine nel punto di lancio e asse y parallelo alla verticale terrestre, positivo verso l’alto.
b) se nel suo moto la palla toccherà il soffitto della palestra.
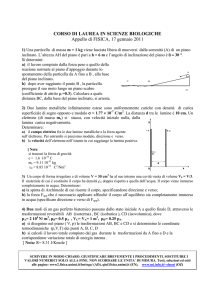
2) Un corpo di massa m=500 g poggia nel punto A su un piano inclinato di 300. Il piano è scabro ed i
coefficienti di attrito statico e dinamico sono uguali e pari a = 0.2.
a) Calcolare la reazione normale N esercitata dal piano sul corpo e la forza Fapp (modulo,
direzione e verso) che deve essere applicata per mantenere il corpo in equilibrio e fermo;
b) Supponendo ora di rimuovere tale forza, calcolare l’accelerazione di cui risente il corpo e lo
spazio percorso lungo il piano, partendo da fermo, dopo un tempo t = 1 s.
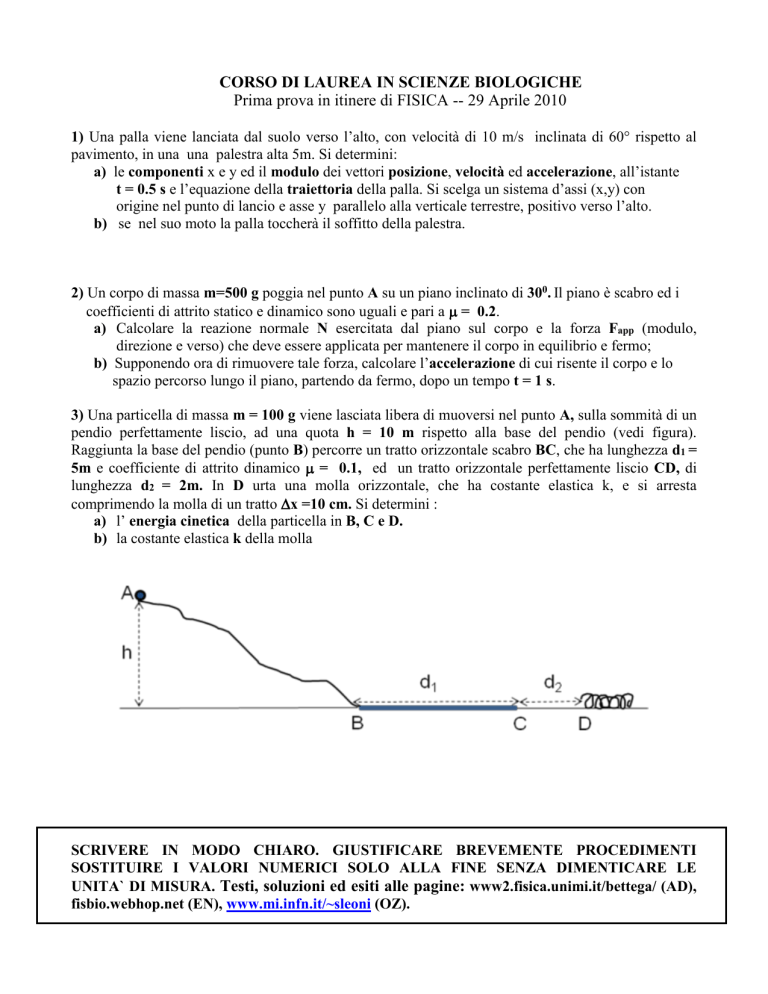
3) Una particella di massa m = 100 g viene lasciata libera di muoversi nel punto A, sulla sommità di un
pendio perfettamente liscio, ad una quota h = 10 m rispetto alla base del pendio (vedi figura).
Raggiunta la base del pendio (punto B) percorre un tratto orizzontale scabro BC, che ha lunghezza d1 =
5m e coefficiente di attrito dinamico = 0.1, ed un tratto orizzontale perfettamente liscio CD, di
lunghezza d2 = 2m. In D urta una molla orizzontale, che ha costante elastica k, e si arresta
comprimendo la molla di un tratto x =10 cm. Si determini :
a) l’ energia cinetica della particella in B, C e D.
b) la costante elastica k della molla
SCRIVERE IN MODO CHIARO. GIUSTIFICARE BREVEMENTE PROCEDIMENTI
SOSTITUIRE I VALORI NUMERICI SOLO ALLA FINE SENZA DIMENTICARE LE
UNITA` DI MISURA. Testi, soluzioni ed esiti alle pagine: www2.fisica.unimi.it/bettega/ (AD),
fisbio.webhop.net (EN), www.mi.infn.it/~sleoni (OZ).
SOLUZIONE ESERCIZIO 1
a) Le componenti dei vettori accelerazione, velocità, e posizione sono rispettivamente:
ax = 0; a y = -g = -9.8 m/s 2 , costanti nel tempo. Il modulo dell’accelerazione a, costante nel tempo, è
/a/=(ax 2 + ay 2) ½ = 9.8 m/s2 .
vx = vox = /vo/ cos 60° =10 /2 = 5 m/s, costante nel tempo;
v y = -g t + voy = -g t + /vo/ sen 60° =
-g t + 8.66.
All’istante t = 0.5 s, vy = 3.76 m/s ed il modulo del vettore velocità è /v / = (vx 2 +vy 2 )½ = 6.26 m/s.
x =voxt = 5t ;
y = - ½ g t 2 + voy t = - 4.9 t 2 +8.66 t.
All’istante t = 0.5 s, x = 2.5 m ; y = 3.1 m ed il modulo del vettore posizione è /r/ = (x2 +y2)½ =
3.98 m.
L’equazione della traiettoria si ottiene dalle relazioni x = 5t e y = - 4.9 t 2 +8.66 t , eliminando il
tempo:
y = - 4.9 (x/5) 2 +8.66 (x/5) = - 0.196 x2 +1.732 x
b) La palla raggiunge la massima quota all’istante in cui vy = 0 , cioè per t = 8.66/g = 0.88 s. La
massima quota è pertanto y = - 4.9 (0.88)2 + 8.66(0.88)=3.8m, minore dell’altezza della palestra.
Pertanto la palla non raggiungerà il soffitto.
SOLUZIONE ESERCIZIO 2
a) Per calcolare la reazione N e la forza da applicare per mantenere il corpo in equilibrio utilizziamo la
seconda legge di Newton, proiettandola sugli assi x ed y, secondo lo schema mostrato in figura:
F Fg N Fs Fapp 0
Fx mg sin Fapp Fs 0
Fy mg cos N 0
da cui si ottiene
N = mg cos (0.5 kg)(9.8m/s2) cos(300)
Fapp = mg sin - N = mg (sin - cos
= (0.5 kg)(9.8m/s2) (sin(300) – 0.2 cos(300)) = 1.6 N
La forza Fapp ha modulo 1.6 N, è diretta parallela al piano inclinato ed in verso opposto all’asse x,
come indicato in figura.
b) Se si rimuove la forza Fapp il corpo è soggetto alla forza peso, alla forza normale ed alla
forza di attrito dinamico.
Per calcolare l’accelerazione a cui è soggetto il corpo applichiamo di nuovo l’equazione della
dinamica:
F Fg N Fs ma
Fx mg sin Fs ma
Fy mg cos N 0
da cui si ottiene
mg sin mg cos ma
a g (sin cos ) Fapp / m 3.2 m / s 2
Dopo t = 1 s il corpo ha percorso una distanza
d = ½ a t2 = ½ × 3.2 × (1)2 m = 1.6 m
SOLUZIONE
ESERCIZIO 3
a) L’energia cinetica nel punto B può essere ricavata facilmente applicando il teorema di
conservazione dell’energia meccanica ai punti A e B in quanto l’unica forza agente che compie
lavoro durante la discesa della particella lungo il pendio, è la forza Peso, conservativa. Si ha
pertanto :
EcinB = mgh = 9.8 J
Nel tratto BC , l’unica forza che compie lavoro è la forza d’attrito F = - mg i, dove i è il
versore dell’asse x , scelto coincidente con la direzione e verso del moto. Per il teorema lavoroenergia cinetica , il lavoro LBC compiuto dalla risultante delle forze agenti ( in questo caso la
forza d’attrito) uguaglia la variazione dell’energia cinetica EcinC - EcinB . Si ha pertanto :
LBC = - mg d1= EcinC - EcinB da cui si ricava EcinC = LBC + EcinB = - 0.49 +9.8 = 9.31 J
Nel punto D l’energia cinetica è uguale a quella del punto C , EcinD = 9.31 J.
b) Quando il corpo si è arrestato e la molla risulta compressa di 10 cm, tutta l’energia cinetica del
sistema è diventata energia potenziale associata al campo della forza elastica esercitata dalla
molla (la forza elastica è una forza conservativa).
Si ha quindi EcinD = ½ k (x) 2 , da cui si ricava k = 2 EcinD / (x) 2 = 1862 N/m