CORSO DI LAUREA IN SCIENZE BIOLOGICHE
II compitino di FISICA, 20 Giugno 2011
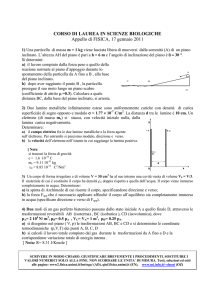
piana infinitamente estesa , uniformemente carica con densità = + 4 10-8 C/m2 è perpendicolare
all’asse x di un sistema di assi (x,y) di origine O e passa per B di coordinate (+2m, 0). Una carica negativa
q = - 2 10-8 C viene lasciata libera di muoversi nell’origine O.
Si determini :
a) il campo elettrostatico, specificando modulo direzione e verso, in O e nel punto C di coordinate (+4m, 0);
b) l’energia cinetica con cui la carica q raggiunge la lamina nel punto B e, supponendo che in B sia praticato un
forellino di dimensioni tali da non perturbare il campo elettrostatico, l’energia cinetica di q nel punto C;
c)Facoltativo: La carica q ripasserà per O ? (giustificare la risposta). Se sì, con quale velocità?
[Nota : 0 = 8.85 10-12 C2/Nm2 ].
1) Una lamina
2) In un liquido ideale di densità l= 2 g/ cm3 galleggia un cubo, di lato L = 10 cm, immerso per il 40% del
proprio volume.Determinare:
a) la spinta Archimedea FA e la densità C del materiale di cui è costituito il corpo;
b) la forza Fapp (modulo, direzione e verso) che è necessario applicare per mantenere il corpo completamente
immerso.
c) Facoltativo: determinare la densità C del materiale nel caso in cui all'interno del corpo sia presente una cavità
vuota, pari alla metà del suo volume. Si supponga sempre che il corpo galleggi con il 40% del proprio volume
immerso.
3) Due moli di un gas perfetto biatomico, inizialmente nello stato A di coordinate termodinamiche pA = 2 atm ,
VA = 5 l, compiono le seguenti trasformazioni termodinamiche:
- AB: decompressione a volume costante fino alla pressione pB = 1 atm;
- BC: espansione isoterma fino al volume Vc = 7 l;
- CD: compressione isobara fino al volume VD = 2 l.
a) Si disegnino le trasformazioni nel piano (p,V) e si determinino le coordinate termodinamiche (p,V,T) per gli
stati A, B, C e D;
b) Si calcoli la variazione di energia interna, il lavoro e il calore scambiato in ogni singola trasformazione e
complessivamente.
[Nota: R= 8.31 J/Kmole =0.082 l atmo /Kmole]
R1) Recupero Cinematica
Un proiettile è sparato in aria con velocità v = 10 m/s e angolo 60° . Determinare le componenti della velocità
del proiettile all'istante del lancio e alla quota massima. Determinare la massima quota h e il tempo t impiegato
per raggiungerla.
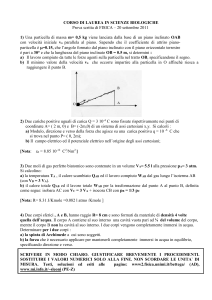
R2) Recupero dinamica Una particella P di massa M= 200 g viene lanciata dalla sommità (punto A) di un piano
liscio inclinato di 30° , rispetto al piano terrestre orizzontale, con velocità iniziale vA = 2 m/s. Il piano inclinato
ha lunghezza AB = 4 m. Dopo il punto B, alla base del piano inclinato, la particella prosegue il suo moto lungo il
piano orizzontale scabro (coefficiente di attrito = 0,1) fino al punto C dove si arresta.
Si determini: l’accelerazione della particella P lungo il piano inclinato, la sua velocità in B ed il tratto BC
percorso lungo il piano orizzontale.
R3) Recupero energia Una particella P di massa M= 200 g viene lanciata dalla sommità (punto A) di un piano
liscio inclinato di 30°, rispetto al piano terrestre orizzontale, con velocità iniziale vA = 1 m/s, parallela al piano
inclinato. Il piano inclinato ha lunghezza AB = 2 m. Dopo il punto B, alla base del piano inclinato, la particella
prosegue il suo moto lungo il piano orizzontale liscio fino al punto C ( BC=1m) dove urta una molla di costante
elastica k= 1000 N/m , inizialmente in equilibrio, e si arresta . Si calcoli la massima compressione della molla.
SCRIVERE IN MODO CHIARO. GIUSTIFICARE BREVEMENTE I PROCEDIMENTI. SOSTITUIRE I VALORI
NUMERICI SOLO ALLA FINE. NON SCORDARE LE UNITA` DI MISURA.
Testi, soluzioni ed esiti alle pagine: www2.fisica.unimi.it/bettega/ (AD), www.mi.infn.it/~sleoni (PE-Z)
SOLUZIONE ESERCIZIO 1 (Elettrostatica)
a) Il modulo del campo elettrostatico creato dalla lamina nel punto O e nel punto C è :
/E/ = / 2 0 = 0.23 104 N/C. In entrambe i casi la direzione è perpendicolare alla lamina ( quindi
parallela all’asse x) . I verso del campo in O è quello di (-i ) , mentre quello del campo in C è il verso
di (+i),
quindi EO = 0.23 104 N/C ( -i )
EC = 0.23 104 N/C ( +i ).
b) La forza elettrostatica agente sulla carica –q nel punto O è F = -q E = 0.46 10-4 N/C ( i ).
L ‘energia cinetica della particella carica quando raggiunge il punto B si calcola facilmente con il
teorema lavoro energia cinetica:
L = F OB = EcnB - EcnO = EcnB = 0.92 10- 4 J.
Nella regione da B ad C la forza è opposta allo spostamento e pertanto la variazione di energia cinetica
è negativa e pari a - 0.92 10- 4 J. L’energia cinetica della carica in C è 0.
c) Facoltativo Nel punto C la forza elettrostatica è F = -q E = 0.46 10-4 N/C (- i ), pertanto la carica
q si rimette in moto verso B con accelerazione costante.
Oltrepassato B la forza F = -q E = 0.46 10-4 N/C ( i ) è opposta alla velocità di q, pertanto q
decelererà fino a raggiungere O con velocità nulla.
SOLUZIONE ESERCIZIO 2 (Fluidi)
a) La spinta di Archimede agisce sul 40% di volume immerso, ossia:
FA = mf g = f Vimm g = 2 10-3 kg/(10-2 m)3 x 0.4 x (0.1 m)3 x 9.8 m/s2 = 7.84 N
La densità del materiale di cui è costituito il corpo si ottiene dalla condizione di galleggiamento:
FA = mf g = f Vimm g = f 0.4 V g = Fg = c V g
Da cui si ottiene:
c = 0.4 f = 0.8 103 kg/m3
b) Per mantenere il corpo completamente immerso è necessario applicare una forza Fapp tale che
Fapp Fg FA 0
Proiettando tale equazione sull’asse verticale di ottiene:
Fapp Fg FA 0
Fapp Fg FA
cVg f Vg ( f c )Vg
1.2 10 3 10 3 9.8 N 11.8 N
La forza Fapp è diretta lungo la verticale in verso opposto all’asse y (ossia concorde con la forza peso).
c) Se il corpo ha al suo interno una cavità vuota di volume V/2, nell'ipotesi che il volume immerso sia
sempre 0.4 V, la spinta di Archimede non cambia, mentre la forza peso è pari a
Fg = c V/2 g
La condizione di galleggiamento diventa quindi:
f 0.4 V g = c V/2 g
da cui si ricava:
c = 2 x 0.4 f = 1.6 103 kg/m3
SOLUZIONE ESERCIZIO 3 (Termodinamica)
a)
Stato A:
pA = 2 atm = 2 x 105 Pa
VA = 5 l = 5 x 10-3 m3
TA = pA VA /(nR) = 60.2 K
Stato B:
pB = 1 atm = 105 Pa
VB = VA = 5 l = 5 x 10-3 m3
TB = pB VB /(nR) = pA/2 x VA /(nR) = TA /2 = 30.1 K
Stato C:
TC = TB = 30.1 K
VC = 7 l = 7 x 10-3 m3
pC = nR TC / VC = 0.71 105 Pa
Stato D:
pD = pC = 0.71 105 Pa
VD = 2 l = 2 x 10-3 m3
TD = pD VD /(nR) = 8.5 K
b)
Trasformazione AB (Isocora):
WAB = 0
Eint)AB = QAB = ncV TAB = 2 x 5/2 R (TB – TA ) = - 1251 J
Trasformazione BC (Isoterma):
DEint = 0
QBC =WBC = nRTB ln(VC/VB) = + 168 J
Trasformazione CD (Isobara):
WCD = pD x (VD – VC) = - 355 J
QCD = ncp TCD = 2 x 7/2 R (TD – TC ) = - 1256 J
DEint = QCD - WCD = -901 J
Trasformazione complessiva (A-> B-> C -> D):
W = WAB + WBC + WCD = - 187 J
Q = QAB + QBC + QCD = - 2339 J
DEint = Q - W = -2152 J
SOLUZIONE R1: RECUPERO CINEMATICA
Le componenti x e y iniziali della velocità del corpo sono:
vx0 = v cos60° = 5 m/s
vy0 = v sin60° = 8.66 m/s
Nel punto di massima quota le componenti della velocità valgono:
vx = vx0 = 5 m/s (moto rettilineo ed uniforme in x)
vy = 0
Il moto è parabolico e la massima quota è raggiunta quanto la componente y della velocità è nulla:
vy = vy0 – gt = 0
t = vyo/g = 0.88 s
quindi
ymax = voy t -1/2 g t2 = 3.83 m
SOLUZIONE R2: RECUPERO DINAMICA
Scelto un sistema d’assi (x,y) in cui l’asse x ha origine in A ed è parallelo al piano inclinato, l’
accelerazione della particella verso B è dovuta alla componente Px della forza peso , parallela al piano
inclinato, dove Px = Mg sen 30° . L’accelerazione è quindi a = g sen 30° = 4.9 m/s2. La velocità in B si
può calcolare utilizzando il teorema Lavoro-Energia cinetica, dove l’unica forza che compie lavoro
lungo AB è Px i = Mg sen 30° (i). Si ha quindi : L = Mg sen 30° AB = EcinB - EcinA = ½ M vB 2 - ½ M vA2
da cui si ricava vB = 6.57 m/s.
Il tratto BC percorso dalla particella lungo il piano orizzontale scabro prima di arrestarsi può essere
calcolato in modo semplice utilizzando il teorema lavoro-energia cinetica:
-M g BC= - ½ M vB 2 da cui si ottiene BC= 22 m
SOLUZIONE R3: RECUPERO ENERGIA
a) Lungo il tratto AB del piano inclinato liscio la forza che compie lavoro è la forza Peso,
conservativa. Pertanto si può calcolare la velocità della particella P in B applicando il teorema di
conservazione dell’energia meccanica. Indicata con h l’altezza OA del piano inclinato si ha:
½ M vA2 + Mgh = ½ M vB2 da cui si ricava vB = 4.5 m/s.
Nel tratto BC de piano orizzontale liscio l’energia cinetica della particella non varia perchè le forze
agenti ( Peso e reazione Normale) non compiono lavoro, pertanto Ecin C = Ecin B. La massima
compressione x della molla si calcola applicando il teorema di conservazione dell’energia
meccanica ( l’unica forza che compie lavoro è la forza elastica che è conservativa):
Ecin C = ½ k x2 dove x è la massima compressione della molla. Da qui risulta x= 6.3 cm.