moti composti 2a parte (moto del proiettile)

Moti composti
Caduta di un grave con velocità iniziale orizzontale
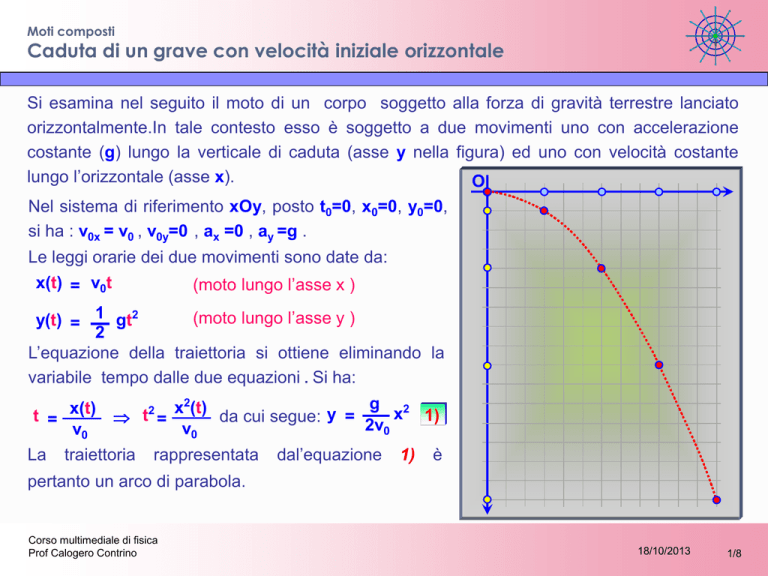
Si esamina nel seguito il moto di un corpo soggetto alla forza di gravità terrestre lanciato
orizzontalmente.In tale contesto esso è soggetto a due movimenti uno con accelerazione
costante (g) lungo la verticale di caduta (asse y nella figura) ed uno con velocità costante
lungo l’orizzontale (asse x).
O
Nel sistema di riferimento xOy, posto t0=0, x0=0, y0=0,
si ha : v0x = v0 , v0y=0 , ax =0 , ay =g .
Le leggi orarie dei due movimenti sono date da:
(moto lungo l’asse x )
x(t) = v0t
(moto lungo l’asse y )
y(t) = 1 gt2
2
L’equazione della traiettoria si ottiene eliminando la
variabile tempo dalle due equazioni . Si ha:
t = x(t)
v0
La
g 2
x2(t)
2
x 1)
y
t
=
da
cui
segue:

=
2v0
v0
traiettoria
rappresentata
dal’equazione
1)
è
pertanto un arco di parabola.
Corso multimediale di fisica
Prof Calogero Contrino
18/10/2013
1/8
Moti composti
Caduta di un grave con velocità iniziale orizzontale
Per determinare in un generico istante t (0 < t < tF ) la velocità del corpo, essendo la velocità
costante lungo l’asse x, basterà determinare la sua componente lungo y come segue: vy = g t
O
Da cui si avrà :
v (t) = vx + vy = v0x i + vy j = v0 i + gt j
e
|v| =

vx
vx 2 + vy 2
V = arctg
Corso multimediale di fisica
Prof Calogero Contrino
vy
vx

gt
= arctg v
0
vy
Con
18/10/2013
2/8
Moti composti
Caduta di un grave con velocità iniziale obliqua
Si esamina ora il moto di un corpo soggetto alla forza di gravità terrestre lanciato con
componenti orizzontale e verticale della velocità. In questo caso il moto sulla verticale avrà
una velocità iniziale mentre si ripeterà la situazione del caso precedente lungo l’orizzontale
Nel sistema di riferimento xOy, (vedi fig.a lato )
posto t0=0, x0=0, y0=0, si ha :
v0x = v0 cos, v0y=v0sen , ax =0 , ay =g .
Le leggi orarie dei due moti sono date da:
x(t) = v0cost
(moto lungo l’asse x)
y(t) = ─ 1 gt2 + v0sent (moto lungo l’asse y)
2
O

L’equazione della traiettoria si ottiene eliminando la variabile tempo dalle due equazioni.
Dalla prima si ha: t =
y = ─
g
2v20 cos2
Corso multimediale di fisica
Prof Calogero Contrino
x2
x(t)
x2(t)
2
e sostituendo nella seconda si ottiene:
t
= 2

v0 cos
v 0 cos2
v0sen
Che è l’equazione della traiettoria cercata.
x
+
1)
v0cos
18/10/2013
3/8
Moti composti
Caduta di un grave con velocità iniziale obliqua
Per t >0 l’equazione 1) rappresenta un arco di parabola la cui concavità è rivolta verso il
g
basso, risulta infatti: ─
<0
2
2
2v 0 cos 
Detto G il punto in cui la traiettoria interseca
l’asse orizzontale (vedi fig.a lato ),si definisce
gittata la distanza OG = xG . Per determinarla
si risolve il sistema:
y= 0
y=
g
sen
x −
x2
2
2
cos
2v0 cos 
O
G





g
g
sen
2
x = 0
da cui segue : x  sen −
x −
x
0
=
2 cos2
2
2
cos
2V
cos
0
2v0 cos 

Si ha quindi: x = 0 → x0 = 0 ( ascissa del punto di lancio )
oppure :
g
g
sen
sen 2V02 cos2
sen
x
x
x
x
=
→
−
=0 →
= G=
cos
cos
2V02 cos2
cos g
2V02 cos2
La risolvente è :
Semplificando si ha infine:
Corso multimediale di fisica
Prof Calogero Contrino
2
2
V
sen2
V
2sen
cos
0
0
xG =
=
g
g
18/10/2013
4/8
Moti composti
Caduta di un grave con velocità iniziale obliqua
Per la simmetria della traiettoria , l’ascissa del punto in cui si raggiunge l’altezza massima è :
2sen cos V02
sen2 V02
xHm = xG =
=
2
2g
2g
L’altezza massima raggiunta dal proiettile si
ottiene sostituendo xHm nell’equazione della
traiettoria.
Pertanto da : y = −
g
sen
2
x
x
+
cos
2v02cos2
O
Si ha successivamente :
=
Hm
=−


y
 sen cos V02
g
2v02cos2 
g
Hm
2
G
xHm
sen sen cos V02
+ cos
=
g
sen2 V02
sen2 V02
sen2 cos2 V04
sen2 V02
sen2 V02
+
+
=−
=−
=
g
2g
g
g2
g
2v02cos2
g
Corso multimediale di fisica
Prof Calogero Contrino
18/10/2013
5/8
Moti composti
Caduta di un grave con velocità iniziale obliqua
Si determina ora l’istante tF in cui viene colpito il bersaglio (si noti che avendo posto in
precedenza t0 = 0 ne segue che l’intervallo t = tF – t0 = tF , esso è detto tempo di volo ).
Dalla relazione : t = x
v0x
vx

vy
Sostituendo ad x l’espressione della gittata si
avrà successivamente :
2sen cos V02
2senV0
tF = xG =
=
v0x
g
V0 cos g
Il tempo impiegato per raggiungere l’altezza
=
massima, pari alla metà di tF, sarà dunque
sen V0
O
dato da : tHm = tF
g
G
2
Per determinare in un generico istante t ( 0 < t < tF ) la velocità del proiettile, essendo la
velocità costante lungo l’asse x, basterà determinare la sua componente lungo y come segue:
Vy = V0y − g t = V0sen − g t e il vettore velocità sarà : V = Vx i + Vy j
Con
|V| =

Vx 2 + Vy 2 e V = arctg Vy
Corso multimediale di fisica
Prof Calogero Contrino
Vx
18/10/2013
6/8
Moti composti
Moto del proiettile – parabola di sicurezza
Si determina ora l’istante tF in cui viene colpito il bersaglio (si noti che avendo posto in
precedenza t0 = 0 ne segue che l’intervallo t = tF – t0 = tF , esso è detto tempo di volo ).
Dalla relazione : t = x
v0x
vx

vy
Sostituendo ad x l’espressione della gittata si
avrà successivamente :
2sen cos V02
2senV0
tF = xG =
=
v0x
g
V0 cos g
Il tempo impiegato per raggiungere l’altezza
=
massima, pari alla metà di tF, sarà dunque
sen V0
O
dato da : tHm = tF
g
G
2
Per determinare in un generico istante t ( 0 < t < tF ) la velocità del proiettile, essendo la
velocità costante lungo l’asse x, basterà determinare la sua componente lungo y come segue:
Vy = V0y − g t = V0sen − g t e il vettore velocità sarà : V = Vx i + Vy j
Con
|V| =

Vx 2 + Vy 2 e V = arctg Vy
Corso multimediale di fisica
Prof Calogero Contrino
Vx
18/10/2013
7/8