testo e soluzione

CORSO DI LAUREA IN SCIENZE BIOLOGICHE
Prova scritta di FISICA del 19 Settembre 2013
MECCANICA: Una particella di massa m=0.5 kg viene lanciata dalla base del
piano inclinato OAB con velocità iniziale vo=4 m/s, parallela al piano.
Sapendo che il coefficiente
di attrito tra piano e particella vale
µ=0.1, che l'angolo formato dal piano inclinato con il piano
orizzontale è pari a 30° e che il OB = 0.5 m, si determinino:
a) la variazione di energia cinetica della particella nel tratto OB;
b) la massima quota della traiettoria della particella rispetto al suolo,
dopo aver abbandonato il piano inclinato.
FLUIDI: Un recipiente cilindrico, aperto superiormente, ha diametro pari
a d=1 m. Contiene acqua ed ha sul fondo un foro di sezione S=4 cm2
inizialmente chiuso da un tappo. Quando il tappa viene tolto, l’acqua
esce dal foro con una portata pari a Q=2 l/s. Calcolare:
a) la velocità con cui l’acqua esce inizialmente dal foro e la velocità
dell’acqua in un punto della superficie libera superiore;
b) il volume di acqua inizialmente contenuto nel recipiente;
ELETTROSTATICA:
Due
lamine
metalliche
infinitamente
estese
sono
uniformemente cariche con densità
di carica superficiale di segno
opposto e modulo pari a σ = 3.54 × 10-7 C/m2. La distanza tra le lamine è
d=4 cm. Si consideri un elettrone (di massa me) che si stacca, con
velocità iniziale nulla, dalla lamina carica negativamente e, trascurando
gli effetti della forza di gravita`, si determinino:
a) modulo, direzione e verso del campo elettrico fra le due lamine e
della forza agente sull’elettrone;
b) la velocità dell’elettrone nell’istante in cui raggiunge la lamina.
(qe=1.6 10-19 C, me=9.11 10-31 kg, ε 0=8.85 10-12 C2/Nm2)
TERMODINAMICA: Un gas perfetto monoatomico occupa nello stato A un
volume VA=5.00 l a pressione atmosferica e alla temperatura TA=300 K.
Esso è riscaldato a volume costante fino allo stato B a pressione
pB=3.00 atm. Poi si espande isotermicamente fino allo stato C a
pressione pC=1 atm, ed infine è compresso isobaricamente fino allo
stato iniziale A. Il candidato:
a) disegni nel piano pV il grafico della trasformazione subita dal gas
e si calcolino il numero di moli n di cui è costituito il gas e le
coordinate termodinamiche (p,V,T) degli stati A, B e C;
b) calcoli il calore Q, il lavoro W e la variazione di energia interna
DEint per le trasformazioni AB, BC e CD e per l’intero ciclo. (R=8.31
J/Kmole=0.082 l atm/Kmol)
Gli esiti saranno pubblicati alla pagina qinf.fisica.unimi.it/~paris.
Le prove orali si terranno Ven 20 Set 2013 a partire dale 10:00
nello studio del docente, V piano Edificio LITA, stanza A5/C4.
SOLUZIONE ESERCIZIO MECCANICA
a) Per il teorema del lavoro-energia cinetica, il lavoro compiuto dalla
forza risultante nello spostamento della particella da O a B uguaglia la
variazione di energia cinetica della particella nello spostamento da O a
B. Scelto l’asse x parallelo al piano inclinato e con origine nel punto
O, la componente della forza risultante agente sulla particella che sale
lungo il piano inclinato, parallela all’asse x e pertanto allo
spostamento della particella, è Rx =-mg sen30°-µmg cos 30°. La variazione
dell’energia cinetica della particella nel tratto OB è pari al lavoro
compiuto dalla forza risultante nel tratto OB: Δ Ec = L = Rx OB =-1.44 J.
b) Dopo aver abbandonato il piano inclinato la particella è soggetta solo
all’azione della forza peso, conservativa. Pertanto l’energia meccanica
nel punto B uguaglia quella nel punto C di massima quota C:
Ec(B)+mghB=Ec(C)+mghC dove hB ed
hC sono le quote rispetto al suolo dei
punti B e C, da cui si ricava hC=[Ec(B)+mghB-Ec(C)]/mg. Ec(B) si calcola
facilmente nota l’energia cinetica inizialee la variazione di energia
cinetica calcolata precedentemente Ec(B)=ΔEc+½mvo2=2.56 J. Inoltre: hB=OB
sen30°=0.25 m, Ec(C)=½mvC2=1.92 J con vC=vB cos 30°=2.77m/s, dato che nel
punto di massima quota la velocità della particella è pari alla
componente della velocità iniziale (nel punto B), parallela al piano
orizzontale terrestre. Sostituendo i valori numerici si ottiene quindi
hC=38 cm.
SOLUZIONE
ESERCIZIO 2
a. La portata volumetrica Q, costante, è Q= v S dove v è la velocità del fluido attraverso la sezione S del
condotto . La velocità di efflusso dell’acqua dal foro vF si calcola quindi dalla vF = Q / SF dove SF è la
sezione del foro. Sostituendo i valori numerici si ottiene:
vF = 2 ∗ 10 –3 (m 3 / s) / 4∗ 10–4 (m2) = 5 m/s. Analogamente la velocità alla superficie libera superiore vL
è vL = Q / SL dove SL è la sezione del cilindro. Sostituendo i valori numerici si ottiene : vL = 2 ∗ 10 –3 (m 3 /
s) / 0.5 2 ∗ π (m2 ) = 2.6 ∗10 –3 (m / s).
b. Applicando il teorema di Bernoulli ai punti della superficie libera dell’acqua e a quelli del foro si ha:
½ ρ vL2 + ρg hL = ½ ρ v F2 dove hL è l’altezza dell’ acqua contenuta nel cilindro . Il termine ½ ρ vL2 è
trascurabile rispetto a ½ ρv F2 e pertanto h ≅ ½ v F2 / g = 1.28 m. Il volume di acqua inizialmente contenuto
è pertanto V= SL hL = 0.5 2 ∗ π (m2 ) ∗ 1,28 (m) =1 m3.
SOLUZIONE ESERCIZIO 3
a) Le due piastre piane cariche producono al loro interno un campo


σ 
3.54 ×10 −7 C / m 2 
E=− i =−
i = −(40 ×10 3 N / C ) i
−12
2
2
ε0
8.85 ×10 C / Nm
ossia perpendicolare alle due piastre e con verso dalla piastra positiva a quella negativa.
La forza elettrica subita dall’elettrone è pari a



σ 
3.54 × 10 −7 C / m 2 
−19
−14
Fe = qE = −eE = (−e)(− )i = (1.6 × 10 C )
i
=
(
0
.
64
×
10
N
)
i
ε0
8.85 × 10 −12 C 2 / Nm 2
ossia è diretta lungo x con verso concorde all’asse.
b) L’ accelerazione subita dall’elettrone è unicamente dovute alla forza elettrostatica, originata dal
campo elettrico:



Fe = me a e = −eE
ossia:



eE (1.6 × 10 −19 C )(40 × 10 3 N / C ) 
15
2
ae = −
=
i
=
(
7
.
03
×
10
m
/
s
)
i
me
9.1 × 10 −31 kg
Essendo l’accelerazione costante, il moto all’interno delle due piastre è rettilineo uniformemente
accelerato, per cui il legame fra velocità e posizione (quando l’elettrone urta l’armatura) è dato da:
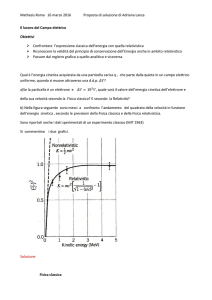
v 2e = v02e + 2a e ( x f − xi ) = 0 + 2a e d = 2a e d
v e = 2a e d = 2(7.03 × 1015 m / s 2 )(0.04m) = 2.37 × 10 7 m / s
SOLUZIONE ESERCIZIO 4
a) Il numero n di moli di cui è costituito il gas si può ricavare
applicando l’equazione dei gas perfetti allo stato A:
p AV A (1.013 × 105 Pa)(5.00 × 10−3 m 3 )
n=
=
= 0.203 moli
RTA
(8.31J / Kmole )(300 K )
Le coordinate termodinamiche degli stati A, B e C
sono le seguenti:
Stato A:
pA = 1 atm = 1.013 x 105 Pa
VA = 5.00 L = 5.00 x 10-3 m3
TA = 300 K
Stato B:
pB = 3 atm = 3 x 1.013 x 105 Pa = 3.039 x 105 Pa
VB = 5.00 L = 5.00 x 10-3 m3
TB = pBVB / nR = (3.039 x 105 Pa) (5.00 x 10-3 m3) / (0.203 moli x 8.31 J/moleK) ≈ 900 K
Stato C:
pC = PA = 1 atm = 1.013 x 105 Pa
VC = nRTC/pC = (0.203 moli x 8.31 J/moleK)(900 K) / (1.013 x 105 Pa) ≈ 15 x10-3 m3 = 15 L
TC = TB = 900 K essendo la trasformazione B→C isoterma
b) Determino ora il lavoro W fatto dal gas, il calore Q scambiato e la variazione di energia interna ΔEint nelle
singole trasformazioni, applicando, ove serva, il primo principio della termodinamica.
A→ B :
WAB = 0 essendo la trasformazione isocora (VA = VB)
( ΔEint )AB= Eint,B – Eint,A
= 3/2 nRTB – 3/2 nRTA
= 3/2 nR(TB -TA)=3/2 (0.203 moli)(8.31 J/moleK)(900-300)K= 1.52 x 103 J
QAB = (ΔEint )AB+ WAB = (ΔEint )AB= 1.52 x 103 J dal il primo principio della termodinamica.
B→ C :
C
C
nRTc
dV
V
B
WBC = ∫ pdV = ∫
B
C
dV
V
=nRTc ln C = (0.203moli ) × (8.31J / Kmole) × 900 K ln 3 = 1.67 × 103 J
V
VB
B
= nRTc ∫
(ΔEint )BC= Eint,C – Eint,B = 3/2 nR(TC –TB)=0 trasformazione isoterma
QBC = (ΔEint )BC+ WBC = WBC = 1.67 x 103 J
C→ A :
A
A
WCA = ∫ pdV = p A ∫ dV = p A (VA − VC ) = (1.013 × 105 Pa) × (5 − 15) × 10−3 m3 = −1.01× 103 J
C
C
(ΔEint)CA = Eint,A – Eint,C = 3/2 nR(TA –TC)= 3/2 (0.203 moli)(8.31 J/moleK)(300-900)K= -1.52 x 103 J
QCA = ΔEint + W = -1.01 x 103 J -1.52 x 103 J = - 2.53 x 103 J
Per l’intero ciclo sommo i contributi relativi alle singole trasformazioni:
WTOT = WAB + WBC + WCA = (0 + 1.67 x 103 – 1.01 x 103) J = -0.66 x 103 J
(ΔEint) = 0 = (ΔEint)AB + (ΔEint)BC + (ΔEint)CA = 1.52 x 103 J + 0 -1.52 x 103 J = 0
QTOT = QAB + QBC + QCA = 1.52 x 103 J + 1.67 x 103 J - 2.53 x 103 J = 0.66 x 103 J