Consideriamo una particella viaggiante lungo l`asse x con energia

EFFETTO TUNNEL
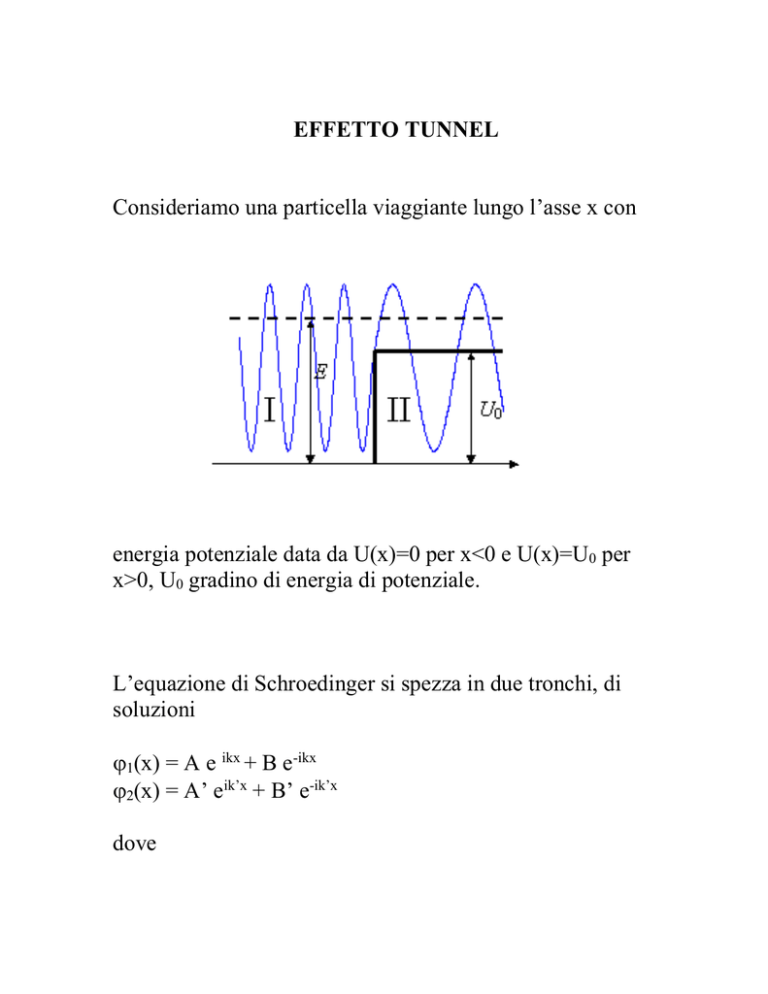
Consideriamo una particella viaggiante lungo l’asse x con
energia potenziale data da U(x)=0 per x<0 e U(x)=U0 per
x>0, U0 gradino di energia di potenziale.
L’equazione di Schroedinger si spezza in due tronchi, di
soluzioni
1(x) = A e ikx + B e-ikx
(x) = A’ eik’x + B’ e-ik’x
dove
k = (2mE) /ħ ,
k’= (2m(E-U0)) / ħ
Osserviamo che B’=0 perché la seconda soluzione non può
avere componenti viaggianti verso valori decrescenti di x.
Imponiamo la continuità in x=0 :
1(0) =(0) e
d1/dx(0) = d2/dx(0).
Si ottengono nella zona 1 due onde sovrapposte, una verso
le x positive (e ikx) e una verso le x negative (e-ikx).
Nella zona 2 si ha un’onda verso le x positive.
L’esistenza dell’onda riflessa è un fenomeno puramente
quantistico, perché classicamente l’onda di fronte al
gradino di potenziale continuerebbe in avanti con energia
cinetica ridotta..
Nel caso E<U0, nella zona 2 la soluzione è del tipo
(x) = A’’ ek’’x + B’’ e-k’’x
con k’’= (2m(E-U0)) / ħ ed esponenziali REALI.
Poichè l’onda non deve divergere per x crescenti, si
impone A’’=0.
La soluzione per la zona 2, con esponenziale decrescente,
evidenzia che la particella penetra per un tratto nella zona
proibita.
La zona è proibita nella meccanica classica perché l’energia
cinetica è negativa.
Tuttavia in meccanica quantistica questo è consentito dal
principio di indeterminazione tempo/energia: la particella
“crea” energia sufficiente per superare la barriera di
potenziale.
Esiste quindi probabilità non nulla che una particella
attraverso la barriera di potenziale.