Mathesis Roma 16 marzo 2016
Proposta di soluzione di Adriana Lanza
Il lavoro del Campo elettrico
Obiettivi
Confrontare l’espressione classica dell’energia con quella relativistica
Riconoscere la validità del principio di conservazione dell’Energia anche in ambito relativistico
Passare dal registro grafico a quello analitico e viceversa
Qual è l’energia cinetica acquistata da una particella carica q , che parte dalla quiete in un campo elettrico
uniforme, quando si muove attraverso una d.d.p. ?
a)Se la particella è un elettrone e
, quale sarà il valore dell’energia cinetica dell’elettrone e
della sua velocità secondo la Fisica classica? E secondo la Relatività?
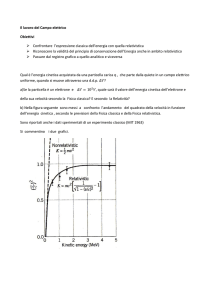
b) Nella figura seguente sono messi a confronto l’andamento del quadrato della velocità in funzione
dell’energia cinetica , secondo le previsioni della Fisica classica e della Fisica relativistica.
Sono riportati anche i dati sperimentali di un esperimento classico (MIT 1963)
Si commentino i due grafici.
Soluzione
Fisica classica
Mathesis Roma 16 marzo 2016
Proposta di soluzione di Adriana Lanza
Supponiamo che un elettrone , la cui carica è q= quella positiva B di un condensatore in cui la d.d.p =
, si muova dalla lastra negativa A a
Il lavoro del campo elettrico è positivo ed è uguale a
potenziale dell’elettrone.
essendo U l’energia
Essendo il campo elettrico conservativo, il lavoro L
su una carica q è sempre uguale alla
diminuzione di energia potenziale e all’aumento di energia cinetica della particella
se la particella parte dalla quiete
Se =
e q= -
allora
=
Relatività
E’ sempre valido il Principio di conservazione dell’Energia ma abbiamo una nuova espressione per l’energia
cinetica
b) Nell’ambito della Fisica classica la relazione tra l’energia cinetica e il quadrato della velocità è di tipo
lineare
essendo m costante
Nell’ambito della Relatività speciale si ha
Posto
la funzione
è definita per x<1,
Il suo grafico passa per l’origine degli assi , è crescente e ammette la retta x=1 come asintoto verticale.
Il grafico della funzione inversa ammette invece un asintoto orizzontale .
Mathesis Roma 16 marzo 2016
Proposta di soluzione di Adriana Lanza
Al crescere di K i valori della velocità crescono sempre più lentamente e il rapporto
tende
asintoticamente al valore 1.
Questi risultati sono coerenti con l’esistenza di una velocità limite, la velocità della luce.
Per valori bassi della velocità v ( nel grafico circa c/2) i due grafici possono essere considerati coincidenti,
cioè le formule della Meccanica classica ben approssimano quelle della Meccanica relativistica.
Per valori alti di v i grafici si discostano e i valori sperimentali sono vicini a quelli della formula relativistica
La relazione
non può essere valida in ambito relativistico.
A l crescere dell’energia, cioè della d.d.p . del campo elettrico che accelera le particelle, non si può avere
un aumento indefinito della velocità.
La relazione
dove
può essere interpretata nel modo seguente
è l’energia a riposo della particella, legata al valore della massa a riposo
.
Ricevendo energia dall’esterno, l’ energia totale della particella diventa
L’incremento di energia comporta un aumento dell’energia cinetica ma anche della massa e quindi
dell’inerzia della particella la cui velocità pertanto non può crescere indefinitamente.