appello-20-09-11b

CORSO DI LAUREA IN SCIENZE BIOLOGICHE
Prova scritta di FISICA – 20 settembre 2011
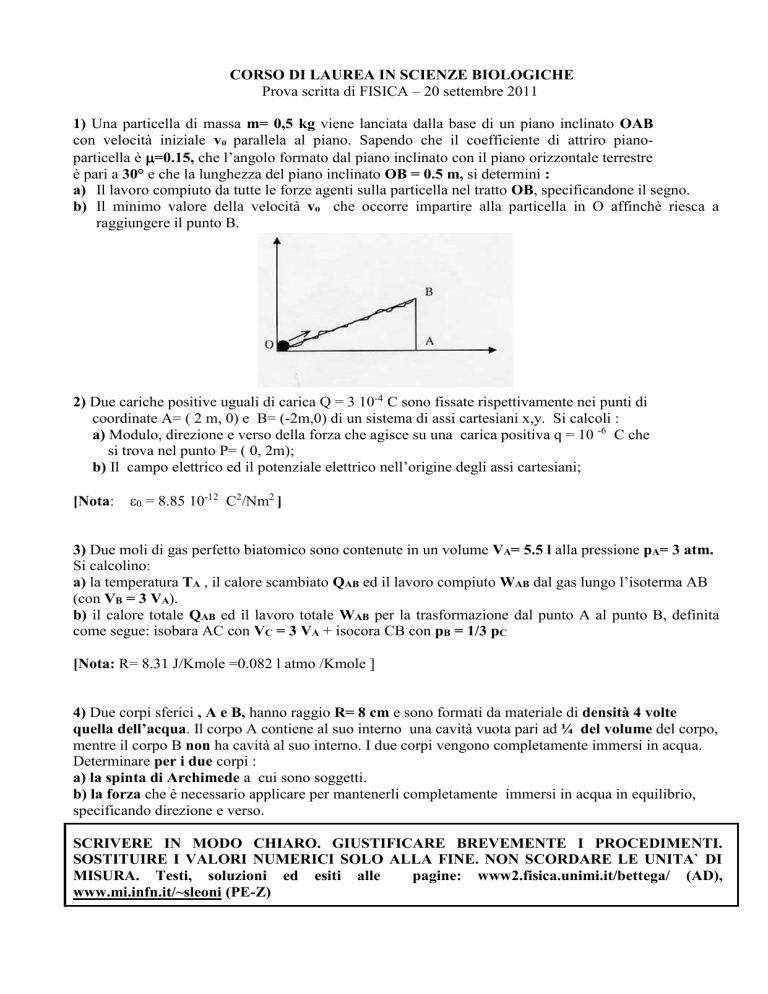
1) Una particella di massa m= 0,5 kg viene lanciata dalla base di un piano inclinato OAB
con velocità iniziale vo parallela al piano. Sapendo che il coefficiente di attriro pianoparticella è =0.15, che l’angolo formato dal piano inclinato con il piano orizzontale terrestre
è pari a 30° e che la lunghezza del piano inclinato OB = 0.5 m, si determini :
a) Il lavoro compiuto da tutte le forze agenti sulla particella nel tratto OB, specificandone il segno.
b) Il minimo valore della velocità vo che occorre impartire alla particella in O affinchè riesca a
raggiungere il punto B.
2) Due cariche positive uguali di carica Q = 3 10-4 C sono fissate rispettivamente nei punti di
coordinate A= ( 2 m, 0) e B= (-2m,0) di un sistema di assi cartesiani x,y. Si calcoli :
a) Modulo, direzione e verso della forza che agisce su una carica positiva q = 10 -6 C che
si trova nel punto P= ( 0, 2m);
b) Il campo elettrico ed il potenziale elettrico nell’origine degli assi cartesiani;
[Nota:
0 = 8.85 10-12 C2/Nm2 ]
3) Due moli di gas perfetto biatomico sono contenute in un volume VA= 5.5 l alla pressione pA= 3 atm.
Si calcolino:
a) la temperatura TA , il calore scambiato QAB ed il lavoro compiuto WAB dal gas lungo l’isoterma AB
(con VB = 3 VA).
b) il calore totale QAB ed il lavoro totale WAB per la trasformazione dal punto A al punto B, definita
come segue: isobara AC con VC = 3 VA + isocora CB con pB = 1/3 pC
[Nota: R= 8.31 J/Kmole =0.082 l atmo /Kmole ]
4) Due corpi sferici , A e B, hanno raggio R= 8 cm e sono formati da materiale di densità 4 volte
quella dell’acqua. Il corpo A contiene al suo interno una cavità vuota pari ad ¼ del volume del corpo,
mentre il corpo B non ha cavità al suo interno. I due corpi vengono completamente immersi in acqua.
Determinare per i due corpi :
a) la spinta di Archimede a cui sono soggetti.
b) la forza che è necessario applicare per mantenerli completamente immersi in acqua in equilibrio,
specificando direzione e verso.
SCRIVERE IN MODO CHIARO. GIUSTIFICARE BREVEMENTE I PROCEDIMENTI.
SOSTITUIRE I VALORI NUMERICI SOLO ALLA FINE. NON SCORDARE LE UNITA` DI
MISURA. Testi, soluzioni ed esiti alle
pagine: www2.fisica.unimi.it/bettega/ (AD),
www.mi.infn.it/~sleoni (PE-Z)
SOLUZIONE ESERCIZIO 1
(Meccanica)
a) Scelto un sistema di assi come in figura , le forze agenti sulla particella nel tratto OB sono la
forza Peso P, che ha componente parallela al piano inclinato Px = -mgsen30°, la forza Normale
N = mgcos30° j e la forza di attrito R=  mgcos30° (-i ). Compiono lavoro diverso da 0 nel
tratto OB: la forza R e la forza Px i, entrambi costanti, parallele ed opposte in verso allo
spostamento OB, i cui lavori compiuti nel tratto OB sono : L(R) = (-  mgcos30° ) OB = - 0.317
J e L (Px i ) = (-mgsen30°) OB = - 1.225 J. Il lavoro totale compiuto è pertanto L = -1.54 J .
b) Affinchè la particella raggiunga B (con velocità nulla) è necessario che la sua energia cinetica
iniziale sia pari al lavoro compiuto dalla risultante delle forze agenti nel tratto OB ( cambiato di
segno) , ovvero a 1.54 J e pertanto che la sua velocità iniziale sia 2.48 m/s.
N
B
R
P
O
A
SOLUZIONE ESERCIZIO 2
(Elettrostatica)
a) La forza elettrostatica totale che agisce
sulla carica q posta in P è data dalla
somma vettoriale delle forze di Coulomb
FAP ed FBP, come disegnato in figura.
Essendo le distanze AP e BP uguali,
tali forze hanno la medesima intensità
F
1
qQ
40 AP 2
Come mostrato in figura, tali forze hanno la
stessa proiezione sull’asse y e proiezioni uguali ed
opposte sull’asse x.
Da ciò segue che la forza elettrostatica totale è un vettore diretto lungo l’asse y di intensità
pari alla somma delle componenti y di ciascuna forza:
4
 1 qQ


 10 6 2 
0
9 3  10

 N  0.48 N
Ftot  2  
cos
45

2

9

10

 40 AP 2

8
2 



ossia:


Ftot  (0.48 N ) j
b) Il campo elettrostatico nell’origine degli assi è nullo, dato che i campi prodotti da
ciascuna carica Q nel punto O hanno stessa intensità
1
Q
E
, stessa direzione e versi opposti.
40 OA 2
Il potenziale in O è dato dalla somma dei potenziali elettrostatici:
V 
1
Q
40 OA

1
Q
40 OB

3  10 4
9

 2
 2   9  10 
40 OA
2

1
Q

V  27  10 5 V

SOLUZIONE ESERCIZIO 3
(Termodinamica)
a) Dalla legge dei gas perfetti si ha TA = pA VA / n R = 100.5 K.
Per l’isoterma AB , QAB = WAB = n R TA ln VB/VA = 1835 J;
b) La seconda trasformazione ha come punto iniziale e finale ancora A e B, poichè l’energia interna
è una funzione di stato e A e B hanno la medesima temperatura , UAB = 0 e dunque QACB =
WACB.
WACB = WAC perchè CB è una isocora WAC = pA (VC -VA) = 2 pA VA = 3343 J = QACB
SOLUZIONE ESERCIZIO 4
(Fluidi)
a) La Spinta Archimedea, pari al peso del fluido spostato , è per entrambi i corpi :
S =  H2O Vsfera g dove H2O = 103 kg / m3 , Vsfera = 4/3 (  R 3 ) e pertanto S = 21 N.
b) Le Forze Risultanti agenti su A e su B, immersi in acqua , sono rispettivamente: FA = PA – S ed FB =
PB – S , dove PA e PB sono le forze Peso agenti su A e su B, PA = 4  H2O 0.75 Vsfera g e
PB = 4  H2O Vsfera g . Sostituendo i valori numerici si trova FA = 42 N ed FB = 63 N , parallele e con
lo stesso verso della forza Peso . Le forze che occorre applicare ad A e B, per mantenerli in equilibrio
in acqua , sono pertanto F*A = 42 N ed F*B = 63 N, parallele e con verso opposto alla forza Peso.