Definizione Integrale Inferiore e Integrale Superiore

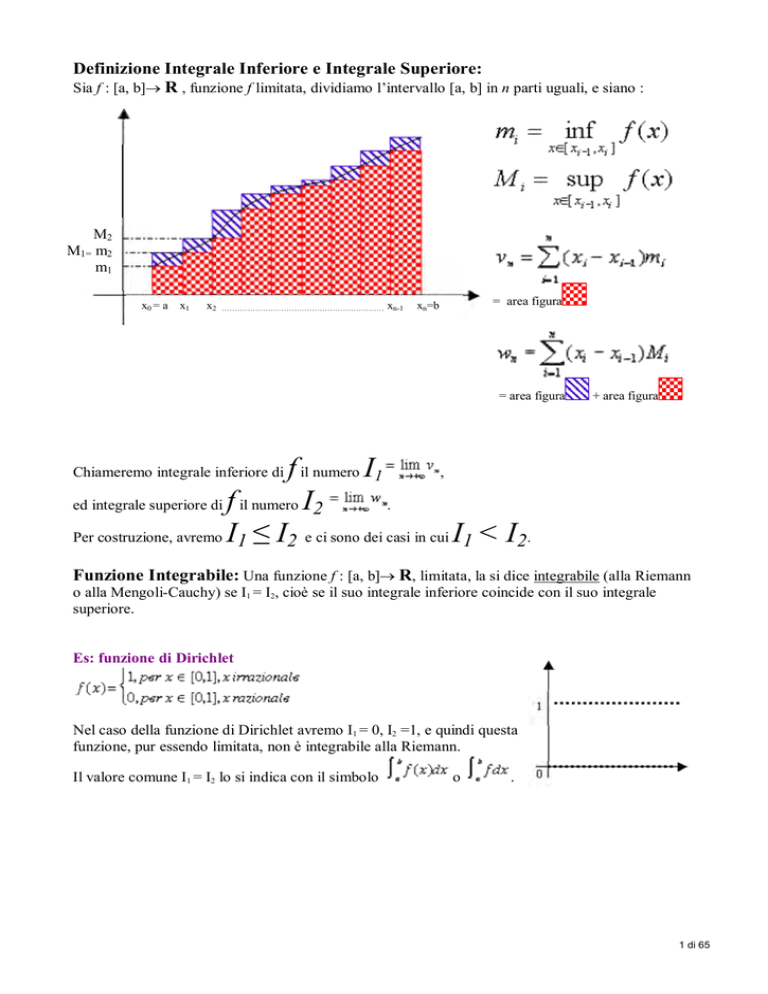
Definizione Integrale Inferiore e Integrale Superiore:
Sia f : [a, b]→ R , funzione f limitata, dividiamo l’intervallo [a, b] in n parti uguali, e siano :
M2
M1= m2
m1
x0 = a
x1
x2
………………………………………………………
xn-1
= area figura
xn=b
= area figura
+ area figura
f il numero I1
,
.
ed integrale superiore di f il numero I2
Per costruzione, avremo I1
I2 e ci sono dei casi in cui I1 < I2.
Chiameremo integrale inferiore di
Funzione Integrabile: Una funzione f : [a, b]→ R, limitata, la si dice integrabile (alla Riemann
o alla Mengoli-Cauchy) se I1 = I2, cioè se il suo integrale inferiore coincide con il suo integrale
superiore.
Es: funzione di Dirichlet
Nel caso della funzione di Dirichlet avremo I1 = 0, I2 =1, e quindi questa
funzione, pur essendo limitata, non è integrabile alla Riemann.
Il valore comune I1 = I2 lo si indica con il simbolo
o
.
1 di 65
Vediamo ora (senza dimostrazione) quali sono le classi di funzioni integrabili (cioè alcune
Condizioni Sufficenti affinché f : [a, b] → R sia integrabile).
• Se f : [a, b] → R è monotona, allora f è integrabile (alla Riemann).
• Se f : [a, b] → R è continua, oppure è limitata ed ha un numero finito di punti di
discontinuità, oppure è limitata ed ha un’infinità numerabile di punti di discontinuità, allora f
è integrabile.
• Se f : [a, b]→ R è discontinua in TUTTI i punti, allora f non è integrabile (alla Riemann).
Vediamo alcune proprietà dell’integrale alla Riemann (senza dimostrazione).
a) Se f : [a, b]→ R è integrabile alla Riemann, allora f è limitata. L’integrale alla Riemann non
viene neppure definito per funzioni illimitate (tra l’altro, le quantità mi ed Mi viste prima,
potrebbero non esistere in R e quindi tutta la costruzione fatta potrebbe non avere senso).
b) Se f1, f2 : [a, b]→ R sono integrabili alla Riemann, allora anche f1 + f2 è integrabile alla
Riemann, e risulta essere:
.
c) Se f : [a, b]→ R è integrabile alla Riemann ed α ∈ R, allora anche α f è integrabile alla
Riemann e si ha:
.
d) Se f1, f2 : [a, b]→ R sono integrabili alla Riemann, allora anche f1 ⋅ f2 è integrabile alla
Riemann (ma non è detto che “l’integrale del prodotto sia uguale al prodotto degli
integrali”!!).
e) Se f1: [a, b]→ R è integrabile alla Riemann ed f2: [a, b]→ R è tale che differisce da f1 solo in
un numero finito di punti, allora f2 è anch’essa integrabile alla Riemann, e i due integrali
coincidono.
f) Se f : [a, b]→ R è integrabile alla Riemann, allora lo è anche | f |, e si ha:
.
Inoltre, se | f | è integrabile alla Riemann, non è detto che f lo sia: basta pensare alla
funzione di Dirichlet definita ponendo
Essa non è integrabile alla Riemann (i suoi punti sono tutti quanti punti di discontinuità), ma
| f (x)| = 1 ∀ x∈[0,1], quindi | f | è integrabile alla Riemann.
Significato Geometrico dell’Integrale: ripensando al significato geometrico
dell’integrale di una funzione positiva e integrabile alla Riemann (integrale = area della
figura delimitata dalla curva y = f (x) avente estremi (a, f (a)) e (b, f (b)), dall’asse x e dalle
rette x = a e
x = b ), si può far vedere che, ∀ k 0,
Si può vedere che anche per k < 0 risulta
(vedi anche Figura 1).
.
2 di 65
Se f è “completamente” negativa, allora l’integrale alla Riemann
è uguale all’area
di cui sopra ma “cambiata di segno”: infatti l’area è sempre definita positiva, mentre
l’integrale di una funzione negativa o nulla è negativo o nullo; invece l’integrale di una
funzione positiva o nulla è positivo o nullo.
g) Se f1 f2, allora
, ammesso che f1, f2: [a, b]→ R siano integrabili alla
Riemann. In particolare, se f : [a, b]→ R è integrabile alla Riemann, allora, se f 0, si avrà
; mentre, se f 0, si avrà
.
h) Se f : [a, b]→ R è continua, f (x) 0 ∀ x ∈[a, b] ed ∃ x’ ∈ [a, b] tale che f (x’)>0, allora
(strettamente positivo).
Durante il corso proveremo alcuni fondamentali teoremi sull’integrale (alla Riemann), tra
cui il teorema della media, quello di Torricelli – Barrow (che afferma che ogni funzione
continua f : [a, b]→ R ammette primitive in [a, b]) e la Formula Fondamentale del Calcolo
Integrale.
i) Se f : [a, b]→ R è integrabile in [a, b], allora f è integrabile in ogni sottointervallo [c,d] di
[a,b]; ed inoltre, se a < c < b, si ha
.
j) (Senza dimostrazione) Se a < c < b, ed f : [a, b]→ R, limitata, è integrabile sia in [a,c] sia in
[c,b], allora f è integrabile anche in [a, b] e risulta essere
k) La Funzione Integrale: Sia f : [a, b]→ R una funzione integrabile. Allora f è integrabile
in ogni intervallo del tipo [a,x], con a x b.
Definiamo la funzione integrale F associata ad f ponendo:
convenzione
N.B.: Se a>b, porremo
, con la
.
(sempre per convenzione).
L’integrale alla Riemann, in letteratura, si chiama integrale definito (per distinguerlo dall’integrale
indefinito che introdurremo tra poco).
3 di 65
Integrale Indefinito:
Definizione: Data una funzione f :I → R (ove I ⊂ R è un intervallo o una semiretta o tutto R), non
necessariamente limitata, si chiama integrale indefinito di f su I la classe delle primitive di f su I,
ammesso che esistano.
Esempio:
Sia I = R, ed f (x) = cos x. Una primitiva di f , in R, è: P(x)=sin x, in quanto D(sin x) = cos x.
Poiché, in un intervallo o semiretta o tutto R (insieme non bucato ), “due primitive differiscono per
una costante”, allora la classe delle primitive di f è data da sin x + c. In simboli matematici, si
scriverà:
.
Si può anche parlare dell’integrale indefinito per funzioni definite su un insieme che è l’unione di
un numero finito di semirette e/o intervalli a 2 a 2 disgiunti, ma bisogna fare qualche
considerazione.
Esempio:
Sia f : R\{0} = ] −∞, 0 [ ∪ ] 0, +∞ [, definita ponendo
. Una primitiva di f , in R\{0}, sarà
P(x) = log |x| . Due primitive, in un intervallo o semiretta o tutto R, differiscono per una costante
(Questo non vale esattamente così in un insieme “bucato”, quale è R\{0}). Quindi: in
] −∞, 0 [ due primitive differiscono per una costante c1; mentre in ] 0, +∞ [ due primitive
differiscono per una costante c2 (in generale, non è detto che c1 e c2 siano la stessa costante). Quindi
sarà dato da
l’integrale indefinito di
c1
al variare di c1 e c2 ∈ R
log |x| +
c1 si riferisce a] −∞, 0 [,
c2
c2 si riferisce a] 0, +∞ [.
Per esempio, una primitiva sarà
Però, in questi casi, per “semplificare”, in letteratura si dice comunque che l’integrale indefinito di
è dato da log |x| + c (anche se, in questo caso, è una scrittura impropria), cioè
.
Adesso vedremo come si calcolano gli integrali indefiniti e poi anche quelli definiti. Innanzi tutto,
dalla tabella fondamentale delle derivate si può ricavare quella fondamentale degli integrali, per
esempio:
x α +1
∫ x dx = α + 1
α
1
∫1+ x
2
, per α ≠ −1
dx = arctgx + c
4 di 65
∫
f ' ( x)
dx = log f ( x) + c
f ( x)
, per α ≠ −1
.
Non c’è una regola ben precisa per il calcolo dell’integrale delle funzioni; tuttavia ci sono alcuni
metodi che ci saranno utili via via durante il Corso. Cominciamo dalla seguente:
Formula di Integrazione per Parti
Siano f, g: [a, b]→ R aventi derivata continua in tutto [a, b]. Allora
;
.
Notiamo che la formula, relativa all’integrale indefinito, vale anche per funzioni definite in un
insieme “di tipo I”, cioè un intervallo, o una semiretta, o tutto R.
Esempio:
Calcolare
.
In questo caso, il “trucco” è quello di “mettere un 1 davanti”.
Si ha:
f (x) = log x g (x) = x
Applicando la formula di integrazione per parti si ottiene:
Prova: faccio la derivata
,
come volevasi dimostrare.
Esempio:
(in questi casi, il “trucco” è quello di ricondursi ad una frazione in cui
il numeratore sia la derivata del denominatore ed applicare la formula
)
.
Prova: faccio la derivata
, come volevasi dimostrare.
5 di 65
Esempio:
. Si ha:
calcoliamo sempre per parti, il seguente integrale indefinito:
.
Prova: faccio la derivata
, come volevasi dimostrare.
Esempio:
(vedi risultato precedente)
.
Prova: faccio la derivata
, come volevasi dimostrare.
Esempio:
. Si ha:
.
Prova: faccio la derivata
, come volevasi dimostrare.
Esempio:
I:=
. Si ha:
I=
I. Dunque I
I, cioè 2I
, da cui I
Prova: faccio la derivata
(trucco:
)
, come volevasi dimostrare.
Esempio:
J:=
. Si ha:
J=
6 di 65
J, ossia J
J, cioè 2J
, da cui J .
Prova: faccio la derivata
come volevasi dimostrare.
Formula di Integrazione per Sostituzione
Oltre all’integrazione per parti esiste anche un altro metodo per l’integrazione (per sostituzione).
Non riporteremo la formula esplicitamente, ma faremo vedere come funziona questo metodo
solamente attraverso qualche esempio, per ragioni di semplicità. Sarà importante la formula:
, oppure
Esempio:
Calcolare K=
.
.
Si ha: K=
…
Adesso, bisogna utilizzare un “trucco”:
(L’operatore “d” si chiama “differenziale” e ha
sostanzialmente lo stesso comportamento della derivata); inoltre la costante moltiplicativa può
essere portata dentro e fuori i segni di derivata e di integrale.
…
Esempio:
. Per sostituzione poniamo
Da ciò si ottiene
. Si ha quindi
, e pertanto
.
, e dunque
Prova:
applicando la formula della derivata del prodotto e quella della derivazione delle funzioni
composte:
, come dovevasi dimostrare.
Esempio:
calcoliamo ora:
:
in queste espressioni (che contengono seno, coseno, tangente), se la potenza in cui compaiono le
suddette funzioni trigonometriche è pari, si adopera la sostituzione
, mentre, se ce n’è
7 di 65
almeno una di ordine dispari, si opera la sostituzione
. Come si ricavano le espressioni sin x
e cos x in funzione di
? Semplicemente applicando l’identità fondamentale
,
ottenendo, per esempio (dove ha senso, naturalmente…):
ed inoltre
.
Come si ricavano le espressioni sin x e cos x in funzione di
Basta ricordarsi le Formule
?
della tangente dell’arco metà
,
,
.
Quindi nel nostro caso, tornando all’integrale
I:=
, si ha:
,
,
,
I:=
,
,
. Facciamo ora la prova. Si ha:
(infatti D (tgw) =
1
* w' ).
cos 2 w
\
Adesso dobbiamo “ritrovare” sin x, cioè
). Si ha pertanto
Inoltre,
volevasi dimostrare.
in quanto sappiamo che
.
(va tutto al denominatore!)
, come
Esempio:
K=
. Ricordiamo che
, (posto tg x = t)
8 di 65
,
,
. Quindi
K=
.
Prova:
, come volevasi dimostrare.
Formula di Hermite
Il prossimo passo è lo studio dell’integrale indefinito per funzioni razionali. Procediamo con alcuni
esempi. Prima di tutto, calcoliamo il seguente integrale indefinito:
I=
Studiamo il trinomio
. Osserviamo che il suo discriminante è 16 − 52 = − 36 < 0, e
pertanto
> 0 ∀ x ∈ R e il nostro trinomio non ammette radici reali. Ora usiamo il
seguente trucco: scriviamo
come “quadrato di un binomio più qualcosa”. Notiamo che
, e quindi si ottiene:
. Tenendo
conto che il differenziale d si comporta analogamente come la derivata, otteniamo:
I=
(Ora si può procedere come nell’esercizio
)
.
Prova:
come volevasi dimostrare.
9 di 65
Esempio:
. Si ha
.
Il trucco (= stato “embrionale”, “iniziale” della formula di Hermite) è porre
(1 e −1 sono radici reali semplici, e quindi si usano due costanti reali A e B).
Si ha pertanto:
.
Si deve determinare A e B in modo tale che (A+B) x − A + B = 0 ⋅ x + 1. Per il principio di identità
dei polinomi, si deve avere
Quindi
.
Prova:
come dovevasi dimostrare.
Pertanto si avrà:
Esempio:
L=
L=
J=
. Si ha
.
Passiamo ora a calcolare
.
Vogliamo ricondurci a una forma del tipo:
1° termine: in cui il numeratore sia la derivata del denominatore.
2° termine: il resto, cioè quello che “avanza”.
Osserviamo che
mentre quello che compare è 4 x + 7.
1°passo: per arrivare da 2 x − 4 a 4 x + 7, innanzi tutto, bisogna moltiplicare per 2.
, quindi
, e dunque
J=
(teniamo ora conto che
∀ x ∈ R)
(Quest’ultimo integrale l’abbiamo già precedentemente calcolato)
10 di 65
.
Prova:
Facciamo la prova, tenendo conto dell’integrale già calcolato in precedenza. Si ha:
, come dovevasi dimostrare.
Esempio:
Per “andare da 2 x a 3 x + 8” bisogna moltiplicare per
. Quindi
, e pertanto
, tenendo conto del risultato dell’integrale calcolato in
precedenza.
Prova:
come volevasi dimostrare.
Adesso abbiamo studiato il caso dell’integrazione di funzioni razionali in cui al denominatore c’è
un polinomio di secondo grado e al numeratore un polinomio al più di primo grado. Se al
numeratore c’è un polinomio di secondo grado o di grado superiore e al denominatore c’è un
polinomio di secondo grado, bisogna eseguire la divisione euclidea tra polinomi: considerando
il resto, effettivamente ci si riconduce al caso in cui (il grado del denominatore è 2 e) il grado del
numeratore è al più uno.
Per esempio, calcoliamo il seguente integrale:
.
Eseguiamo la divisione euclidea tra il numeratore e il denominatore. Si ottiene
Pertanto
, e quindi
.
(già calcolato prima!)
11 di 65
Esempio:
.
Il grado del numeratore non è STRETTAMENTE minore di quello del denominatore, e quindi
dobbiamo eseguire la divisione euclidea. Si ha:
Quindi
, e pertanto
(Quest’ultimo integrale era stato calcolato precedentemente).
Calcolo degli Integrali Indefiniti
Passiamo ora a considerare una generica frazione di polinomi P(x), Q(x), ed esaminiamo l’integrale
indefinito:
.
Osserviamo innanzi tutto, come primissima cosa, che, se il grado di P(x) è maggiore o uguale al
grado di Q(x), allora occorre fare la divisione euclidea, com’è stata fatta negli ultimi esercizi, e ci si
ricondurrà allo studio di un integrale indefinito del tipo
, ove R(x) è un polinomio di
grado STRETTAMENTE minore di quello di Q(x). Quindi, per i nostri scopi, non costituisce una
restrizione il fatto che studieremo soltanto funzioni di polinomi con la proprietà che il numeratore
ha grado inferiore a quello del denominatore.
A questo punto, “decomporremo” il denominatore a seconda delle sue radici: esso può avere radici
reali semplici , radici reali multiple (cioè di una certa molteplicità), radici complesse semplici e
radici complesse multiple. (“Radici complesse” significa che il nostro trinomio in questione ha
discriminante negativo).
Esempio:
Calcoliamo il seguente integrale:
.
Osserviamo che il grado del numeratore è inferiore a quello del denominatore, e
quindi procediamo direttamente senza fare la divisione euclidea.
Il “trucco” è il seguente: alla radice reale 0 (di molteplicità 2) corrisponde la quantità
fosse stato (x + 1)3, la quantità corrispondente sarebbe stata
stato solo x − 5, la quantità corrispondente sarebbe stata
(se ci
; se ci fosse
); alle “radici complesse” “generate”
12 di 65
dal polinomio x2 + 1 corrisponde la quantità
(come al trinomio
positivo e non ammette radici reali, corrisponde la quantità
, che è sempre
).
Pertanto si fa la seguente impostazione:
, ove A, B, C, D sono quattro costanti ( cioè numeri reali) da
determinare. Si ha dunque:
.
Quest’ultima quantità dev’essere uguale a
, cioè, diciamo, a:
. Per il principio di identità tra i polinomi, si deve avere che “i corrispettivi
coefficienti devono essere uguali”, cioè
A+C=0
da cui: A = C = 0
B+D=0
B=1
A=0
D = −1
B=1
e quindi
.
Prova:
Facciamo la prova (che va fatta sempre in esercizi di questo genere!):
, come dovevasi dimostrare.
Ovviamente, in questo esercizio, si poteva fare questa “decomposizione” (che in letteratura si
chiama decomposizione di Hermite) in un modo più facile; ma noi abbiamo seguito questo
procedimento, in quanto lo si dovrà adottare nel caso generale. Calcoliamo ora l’integrale
indefinito:
.
Il procedimento che abbiamo adottato si chiama Formula di Integrazione di Hermite
Lo studente è ora invitato a “cimentarsi” in tutti gli esercizi delle soluzioni dei compiti dati sugli
integrali per parti, per sostituzione e con Hermite.
Teoremi fondamentali del Calcolo Integrale per l’integrale alla
Riemann.
Teorema della media:
Siano f, g : [a, b]→ R due applicazioni integrabili, con g(x)
(oppure g (x) 0 ∀ x ∈ [a, b]).
Tesi: Allora esiste un numero reale ϑ ∈ [m, M], ove
0 ∀ x ∈ [a, b]
,
, tale che
13 di 65
.
Dimostrazione:
Essendo f integrabile, f è anche limitata, e pertanto le quantità m ed M di cui sopra esistono in R.
Ovviamente, per definizione di estremo superiore ed inferiore, si ha
m f (x) M
∀ x ∈ [a, b].
Per ipotesi, g(x) 0 (in maniera analoga si procede se g(x) 0 ∀ x ∈ [a, b]). Moltiplicando i termini
della disuguaglianza per g (x), si ottiene
m⋅ g(x) f (x) g(x) M ⋅ g(x),
∀ x ∈ [a, b].
L’applicazione f ⋅ g è integrabile, in quanto è il prodotto di due funzioni integrabili. Passando
all’integrale, otteniamo:
.
Si considerano ora i seguenti due casi:
1 Caso.
dalle disequazioni precedenti segue che:
, e quindi si ottiene:
∀ϑ ∈ R, e in questo caso la tesi del teorema
della media è soddisfatta per qualunque ϑ ∈ R.
2 Caso.
allora segue che
0 ∀x.
in quanto g (x)
allora il verso della
Consideriamo la disuguaglianza e dividiamo per
disuguaglianza rimarrà inalterato, ottenendo:
,
Posto
, allora si ha m
ϑ
cioè
.
M, ed inoltre
: quindi questo ϑ soddisfa la tesi del teorema della
media.
Teorema della media per funzioni continue:
Teorema: Siano f , g : [a, b]→ R tali che f è continua in [a, b], g è integrabile in [a, b] e g (x)
per ogni x ∈ [a, b] (oppure g (x) 0 ∀ x ∈ [a, b]).
Tesi: Allora esiste x0 ∈ [a, b] tale che
0
.
Dimostrazione: Sappiamo che f è continua in [a, b], e quindi f è anche integrabile in [a, b]. Quindi,
in virtù della versione precedente del Teorema della media, si ha:
, ove ϑ è un numero opportuno compreso tra
ed
.
14 di 65
In virtù del teorema di Weierstrass, poiché f è continua nell’intervallo chiuso e limitato [a, b], allora
le quantità m ed M sono rispettivamente il
ed il
, e quindi m ed M vengono
assunti dalla funzione.
In virtù del Teorema dei valori intermedi, f ammette tutti i valori compresi tra m ed M, e quindi
ammetterà anche il valore ϑ.
Pertanto ∃ x0 ∈ [a, b]: f (x0) = ϑ, e quindi segue
,
come dovevasi dimostrare.
Consideriamo ora il seguente caso particolare: g (x) ≡ 1. Allora i due teoremi possono essere
formulati rispettivamente nel seguente modo:
Teorema: Sia f : [a, b]→ R integrabile, e siano
,
Tesi: Allora ∃ ϑ ∈ [m, M] tale che
Teorema: Sia f : [a, b]→ R continua.
Allora ∃ x0 ∈ [a, b] tale che
.
.
.
Significato geometrico del Teorema della media, per f
0: l’area della regione
tratteggiata in figura è uguale a quella del rettangolo avente base il segmento [a, b] e altezza f (x0)
(che viene appunto
f (x0) ⋅ (b−a)).
Se f non è continua, l’ultima versione del teorema della media, in generale, non vale. Per esempio,
consideriamo la funzione f : [0,2]→ R definita ponendo:
In questo caso a = 0, b = 2.
La funzione f non è continua in x = 1, dato che f (1) = 0,
x = 1 è un punto di discontinuità di prima specie non eliminabile.
Consideriamo la relazione
Si ha:
ma
e pertanto
: b − a = 2, e ricaviamo ϑ.
,
15 di 65
(per quanto detto precedentemente …)
non assume mai il valore
, quindi
, e quindi
, ma f
non è del tipo f (x0) per nessun x0 ∈ [a, b].
Principali proprietà della funzione integrale.
Funzioni Lipschitziane
Definizione: Sia I un intervallo o una semiretta contenuta in R, o tutto R. Si dice che f è
Lipschitziana in I se ∃ L > 0 (detta costante di Lipschitz) tale che
per ogni scelta di x, ∈ I.
Significato geometrico della Lipschitzianità: “La pendenza è limitata”.
Notiamo che ogni funzione Lipschitziana in I è continua in I, ma in generale il viceversa non è vero:
per esempio, basta prendere la stessa funzione ex su tutta la retta reale.
Teorema: La funzione integrale F è Lipschitziana in [a, b].
Dimostrazione: Siano x ed ∈ [a, b] due punti distinti fissati arbitrariamente: senza perdita di
generalità, supponiamo che x > . Per definizione di funzione integrale e in virtù dell’additività
dell’integrale si ha:
,
(per il Teorema della media)
ove
è un valore compreso tra m ed M, ed m, M sono rispettivamente l’estremo inferiore e
l’estremo superiore di f nell’intervallo
avente estremi x ed .
Si ha pertanto
.
Prendendo L =
, si ha
.
Ciò vale per ogni coppia di punti x, ∈ [a, b] (anche quando = x, banalmente…).
Da questo segue che F è Lipschitziana in [a, b], come volevasi dimostrare.
Teorema di Torricelli - Barrow:
Teorema: Se f : [a, b]→ R è continua, allora la funzione integrale F associata ad f è derivabile e si
ha, ∀ x ∈ [a, b], F' (x) = f (x).
Dimostrazione: Fissiamo x, in [a, b] arbitrariamente, con x
; senza perdita di generalità,
supponiamo che x > . Si ha:
16 di 65
(facendo gli stessi passaggi come nel teorema precedente)
, ove ξ è un opportuno punto compreso fra x ed , la cui
esistenza è garantita dalla versione del Teorema della media per funzioni continue, in cui si prende
g (x) ≡ 1.
Quando x →
, si ha che ξ →
e f (ξ )→ f ( ), in virtù della continuità di f . Si ha:
.
derivata destra
Analogamente, considerando il caso x <
, si ha:
.
derivata sinistra
(Ovviamente, se = a, si parlerà solo della derivata destra, mentre se = b si parlerà solo della
derivata sinistra)
Dunque, si ottiene F'( ) = f ( ), ∀ ∈ [a, b].
Vedremo più in là che, se f non è continua, non è detto che valga il teorema di Torricelli - Barrow.
Più precisamente, se è un punto di discontinuità per f , può succedere:
a) che F'( ) non esista;
b) che F'( ) = f ( );
c) che F'( ) esista ma sia diverso da f ( ).
Formula fondamentale del Calcolo Integrale:
Teorema: Sia f : [a, b]→ R una funzione continua, e P una primitiva per f . Allora si ha:
.
Dimostrazione: Per ipotesi f è continua in [a, b], e quindi, in virtù del teorema di
Torricelli-Barrow, la sua funzione integrale
è una primitiva di f . Ma due qualsiasi
primitive (relativamente all’intervallo [a, b]) differiscono per una costante (questa è una
conseguenza del Teorema di Lagrange), e quindi, presa comunque una primitiva P di f , esiste una
costante k (dipendente ovviamente da P) tale che P(x) − F(x) = k ∀ x ∈ [a, b]: quest’ultima
uguaglianza vale in particolare anche se al posto di x ci mettiamo a e anche se al posto di x ci
mettiamo b.
Pertanto P(a) − F(a) = k, P(b) − F(b) = k.
Ma
, e quindi P(a) = k; da P(b) − F(b) = k si ottiene P(b) − F(b) = P(a), cioè
F(b) = P(b) − P(a).
Ma F(b) è la funzione integrale calcolata nel punto b, cioè
;
pertanto otteniamo, in definitiva:
,
che era quello che dovevamo dimostrare.
Esempio:
17 di 65
Usando la formula fondamentale del Calcolo Integrale (che abbrevieremo F.F.C.I.), calcolare il
seguente integrale definito:
.
Si ha:
, ove P è una primitiva della funzione seno: per esempio P(x)=−cosx.
Quindi: P(π) = −cos π = −(−1) = 1; P(0) = −cos 0 = −1; P(π) − P(0) = 1 −(−1) = 1 + 1 = 2, e pertanto
, come volevasi dimostrare.
In matematica si usa anche la seguente notazione, a nostro avviso più sintetica e più “comoda”:
.
Quindi la notazione
oppure
sta a indicare la quantità P(b) − P(a).
La F.F.C.I. stabilisce un legame fondamentale tra l’integrale definito
indefinito (perché quest’ultimo è proprio la classe delle PRIMITIVE).
e l’integrale
Esempio:
y
t
x
Calcolare l’integrale definito
.
Suggerimento: Fare la sostituzione x = cos t .
Si ha:
, in quanto t varia da 0 a π
(t è anche l’angolo nella prima di queste due figure), e lì il seno è
sempre una quantità positiva o nulla. Quindi, facendo l’integrale
indefinito, si ottiene:
.
Adesso facciamo una considerazione. Nella formula di “integrazione per sostituzione”, quando è in
gioco l’integrale definito (cioè quello alla Riemann), bisogna “cambiare gli estremi”. Nel nostro
caso particolare, si avrà
in quanto, quando x varia tra –1 ed 1, t varia tra π e 0 (dico “tra π e 0” e non “tra 0 e π”, perché
l’estremo corrispondente a –1 è π, in quanto cos π = –1, mentre l’estremo corrispondente ad 1 è 0,
in quanto cos 0 = 1; bisogna stare molto attenti perché conta non solo l’intervallo costituito dai
nuovi estremi, ma anche l’ordine in cui vengono presi questi nuovi estremi!). Quindi, continuando,
si ha:
,
(questo, in virtù della F.F.C.I.)
che è il risultato che ci si doveva aspettare, perché, in base al significato geometrico dell’integrale,
non è altro che l’area del semicerchio nord di centro l’origine e raggio 1.
18 di 65
Quindi, in questo esercizio:
1) abbiamo applicato la F.F.C.I.;
2) abbiamo usato l’integrazione per sostituzione;
3) abbiamo visto il significato geometrico dell’integrale;
4) ci siamo imbattuti in una formula del tipo
, con a > b .
Esempio:
Calcolare l’area della regione di piano delimitata dalla curva y = sin x e dalle rette x = 0
(asse delle y), x = 2π ed y = 0 (asse delle x).
Nel 1° pezzo (A1) la funzione y = sin x è positiva, e quindi l’area
della figura A1 coincide con:
.
Nel 2° pezzo (A2) la funzione y = sin x è negativa, e quindi l’area
della figura A2 sarà uguale a :
.
Qui, bisogna cambiare il segno!
Quindi, nel 2° pezzo, l’integrale è negativo, ma l’area è POSITIVA. L’area richiesta è dunque la
somma delle aree delle due figure A1 ed A2, e quindi 2 + 2 = 4 e non 0, mentre
(si può arrivare a questa conclusione anche
osservando che
). Notiamo
quindi, nel caso di funzioni non sempre positive, la sostanziale differenza fra integrale ed area!!!
(I due concetti coincidono, invece, per funzioni sempre positive, o comunque non negative).
Ritorniamo ora alle proprietà della funzione integrale
, quando f presenta dei punti
di discontinuità. Cominciamo con il calcolare la funzione integrale F associata alla seguente
funzione f : [−1,1]→ R:
Notiamo che il punto 0 è, per f, un punto di discontinuità di Prima Specie Non Eliminabile.
Il fatto che f (0) = 0 è ininfluente ai fini del calcolo di F.
Per x ∈ [−1,0], si ha:
oppure F(x) = area cambiata di segno del rettangolo avente
base x − (−1) = x + 1 e altezza 1 (nella figura, rettangolo
tratteggiato in questo modo:
).
Per x ∈ ]0,1], nel calcolare la funzione integrale bisogna
tenere conto che f ha due leggi e che, in corrispondenza
del punto 0, f “cambia di legge”.
Occorrerà dunque usare l’additività dell’integrale (trucco fondamentale!) e, per x ∈ ]0,1],
esprimere la funzione integrale nel seguente modo:
.
Abbiamo utilizzato la legge f (t) = −1 per t ∈ [−1,0[ e la legge f (t) = 1 per t ∈ ]0,1]
19 di 65
Pertanto
, e quindi
.
Dimostriamo ora che F non è derivabile in 0. Consideriamo dapprima la derivata destra. Si ha:
in virtù di una nota conseguenza del teorema di Lagrange.
Analogamente, considerando la derivata sinistra, si ottiene
.
In 0, le due derivate destra e sinistra sono diverse: pertanto 0 è punto di non derivabilità per F.
Quindi 0 è un punto di discontinuità per f ed è tale che F'(0) non esiste (siamo nel caso a) di cui
sopra).
Consideriamo ora i casi b) e c).
Sia f : [−1,1]→ R definita ponendo
Notiamo innanzi tutto che f (0) = 1, f è limitata, e il
punto 0 è un punto di discontinuità di seconda specie:
infatti
non esiste, in quanto la restrizione
costituita dai punti del tipo
, con n ∈ IN, “ammette
limite 0”, ma
.
Quindi
non esiste, perché “ci sono due restrizioni aventi limiti diversi” (cioè
rispettivamente 0 e 1).
Sia ora h (x) ≡ 1 (h : [–1, 1]→ R): allora f ed h sono limitate; inoltre f ed h differiscono solamente in
un’infinità numerabile di punti. Pertanto si ha, ∀ x ∈ [−1,1]:
(allo stesso risultato si perviene
considerando il significato geometrico dell’integrale…), e quindi F'(x) = 1 ∀ x ∈ [−1,1].
In particolare si ottiene:
F'(0) = 1 = f (0),
e siamo quindi nel caso b) di cui sopra: cioè, pur essendo 0 un punto di discontinuità per f , abbiamo
che la funzione integrale F è derivabile in 0 e che F'(0) = f (0).
Se si considera invece la funzione f : [−1,1]→ R, definita ponendo
procedendo analogamente come nel caso precedente, si ha che:
• 0 è un punto di discontinuità di 2a specie per f ;
• F(x) = x + 1 ∀ x ∈ [−1,1] e quindi F'(x) = 1 ∀ x ∈ [−1,1], e pertanto F'(0) = 1 0 = f (0),
e siamo perciò nel caso c) di cui sopra, ossia: la funzione integrale F è derivabile in 0,
20 di 65
ma F'(0) f (0).
Dunque, in presenza di un punto di discontinuità di f , può succedere di tutto per quanto riguarda il
comportamento della funzione integrale F.
Esercizio:
Calcolare l’area della regione piana compresa
tra le due curve di equazione:
ed
.
Determiniamo intanto i punti di intersezione
delle due curve, tenendo conto che dobbiamo
imporre preliminarmente la condizione x 0.
Si deve avere:
, x = 0 (e quindi y = 0) oppure:
,
,
,
, x = 4 ed, in corrispondenza a questo valore di x, si trova
oppure
.
Pertanto il punto P in figura ha coordinate (4,4).
Vediamo, per 0 x
Si ha, per esempio:
4
4, chi è “più grande” tra le quantità
ed
.
(considerando x > 0) se e solo se
x ; nel punto 0 si ha banalmente l’uguaglianza. Quindi, per x compreso fra 0
e 4, la funzione delle due (date nell’esercizio) che sta “di sopra” è
, cioè
, mentre quella che sta
“di sotto” è
.
“Completiamo” quindi il disegno nel modo seguente:
P = (4,4)
21 di 65
In virtù del significato geometrico dell’integrale, l’area della regione piana richiesta, che è quella
tratteggiata, sarà uguale alla differenza tra i due integrali
I1 =
ed I2=
. Si ha:
;
I1 =
I2 =
.
Quindi l’area della regione piana richiesta è uguale a
.
Esercizio:
Calcolare l’area della regione di piano limitata dalle due parabole di equazioni:
Determiniamo innanzi tutto i punti di intersezione delle due parabole. Si deve avere:
, ossia
, da cui x = 0 oppure 2 x − 4 = 0, cioè x = 2.
In corrispondenza ad x = 0 si troverà il valore y = 2, mentre in corrispondenza ad x = 2 si troverà
y = 4− 6 + 2 = 0, oppure y = − 4 + 2 + 2 = 0.
Un’altra cosa che si deve fare è vedere quando le funzioni considerate sono positive e quando sono
negative, in quanto, a seconda del segno, la relazione fra integrale ed area cambia.
Studiamo il trinomio
:
Quindi questo trinomio sarà positivo per x ∈ ]−∞, 1[∪]2, +∞ [, negativo in ]1, 2[ e si annulla nei
punti x = 1 ed x = 2.
Studiamo ora il trinomio
:
Le radici sono −1 e 2.
22 di 65
Il trinomio sarà positivo per x ∈ ]−∞, −1[∪]2, +∞ [, negativo per x ∈ ]− 1, 2[ e si annulla nei punti
x = −1 ed x = 2.
Pertanto la quantità
sarà positiva per x ∈ ]−1, 2[, negativa per x ∈ ]−∞, −1[∪]2, +∞ [ e
si annulla per x = −1 ed x = 2.
A questo punto, facciamo un disegno “esplicativo”:
La nostra area sarà uguale alla somma dell’area A1 e dell’area A2.
ed
L’area A1 sarà data dalla differenza tra
, cioè:
Area A1 =
applicando la F.F.C.I.
.
L’area A2 sarà data da
, in quanto, nella zona A2, l’integrale è negativo, e quindi
bisogna effettuare un cambio di segno. Si ha:
Area A2 =
.
.
Pertanto l’area richiesta sarà data da Area A1 + Area A2
Esercizio:
Calcolare l’area della regione di piano compresa tra la parabola di equazione
, la retta di
equazione
e l’asse delle x (cioè la retta y = 0).
Soluzione: Imponendo la condizione x 0, determiniamo i punti di intersezione tra la retta y = 4 −
2x e la parabola
. Si ottiene:
, cioè
, da cui
.
Poniamo
: si ottiene
Il valore −2 è da evitare (perché abbiamo posto
e quindi t 0). Quindi otteniamo t = 1, cioè
x = 1. In corrispondenza ad x = 1 si ottiene y = 2. Pertanto il punto (1,2) è l’unico punto di
intersezione tra la parabola
e la retta y = 4 − 2x.
Inoltre 4 − 2x = 0 ⇔ x = 2. Facciamo quindi un disegno della figura:
23 di 65
L’area A della figura richiesta sarà data dalla somma delle due quantità I1 e I2 ove
I1 =
mentre I2 è l’area del triangolo avente come
vertici i punti (1,0), (2,0) e (1,2): la base e l’altezza misurano rispettivamente 1 e 2, e quindi l’area
di questo triangolo sarà
. Quindi A = I1 + I2
.
Ora facciamo un confronto tra l’integrale indefinito e l’integrale definito: vedremo che non sono
esattamente la stessa cosa. Più precisamente mostreremo che esistono funzioni che ammettono
primitive ma non sono integrabili alla Riemann (in [a, b]), e che esistono altre funzioni che sono
integrabili alla Riemann ma non ammettono primitive (in [a, b]). Cominciamo con il seguente:
Esercizio:
Calcolare la derivata della funzione f : [−1,1]→ R che è definita ponendo:
Per x 0 si ha:
Inoltre, per x = 0, si ha:
.
limitata=0.
Quindi
24 di 65
Ovviamente, f ' ammette primitive in [−1,1] (la f !!), ma non è integrabile in [−1,1], in quanto non è
ivi limitata (la presenza del fattore
punto 0).
vicino a 0 rende illimitata la funzione f ' in prossimità del
D’altro canto, consideriamo la funzione:
h è integrabile in [−1,1], e, in base al significato geometrico
dell’integrale, la quantità
è uguale all’area del quadrato
tratteggiato in figura, cioè a 1 ⋅ 1 = 1; h non ammette primitive in
[−1,1], in quanto, se le avesse, h godrebbe della proprietà dei
valori intermedi (in virtù del Teorema di Darboux), cosa che in
questo caso non è vera.
Integrale Generalizzato o Improprio
Passiamo ora a “estendere” il concetto di integrale alla Riemann a funzioni definite in un intervallo
chiuso e limitato [a, b], ma ivi non necessariamente limitate, e poi anche a funzioni definite in una
semiretta del tipo [a, +∞[ oppure ]−∞, b] o tutto R.
Sia f : [a, b]→ R con le seguenti proprietà:
• definita in [a, b] tranne che, al più, nel punto b;
• illimitata solamente (al più) in prossimità di b;
• integrabile secondo Riemann in [a, x] ∀ x ∈ ]a,b[.
Diremo che f è Integrabile in Senso Generalizzato in [a, b] se esiste in R il limite
x
lim ∫ f (t )dt (se viene ± ∞, non lo è).
x →b − a
Sia f : [a, b]→ R:
• definita in [a, b] tranne che, al più, nel punto a;
• illimitata solo (al più) in prossimità di a;
• integrabile secondo Riemann in [x, b] ∀ x ∈ ]a,b[.
Diremo che f è Integrabile in Senso Generalizzato in [a, b], se esiste in R il limite
b
lim ∫ f (t )dt .
x→a + x
Osservazione: Notiamo che tutte le funzioni integrabili alla Riemann sono integrabili in senso
generalizzato (in quanto la funzione integrale è continua, dato che essa è addirittura Lipschitziana),
ma non è vero il viceversa.
25 di 65
Esempio:
Calcoliamo il seguente integrale definito:
.
La funzione
è definita in ]0, 1] ed è illimitata in prossimità del punto 0. Si ha:
R
.
Quindi la funzione
è integrabile in senso generalizzato in [0, 1]:
Vediamo ora che cosa succede nello stesso intervallo per la funzione
.
. È:
.
Quindi la funzione
non è integrabile in senso generalizzato in [0, 1].
, con α > 0, nell’intervallo ]0, 1].
Più in generale, consideriamo la funzione
Caso α > 1.
.
Per α > 1, 1 − α < 0, quindi
,
numero negativo = +∞.
Pertanto, per α > 1, la funzione
non è integrabile in senso generalizzato in [0, 1].
Caso 0 < α < 1:
Procedendo come nel caso precedente, si ottiene:
. Questa volta 1 − α > 0, e quindi
; quindi, per 0 < α < 1, la funzione
, e pertanto si ha
è integrabile in senso generalizzato in [0, 1].
Abbiamo già visto che, per α = 1, la funzione
non è integrabile in senso generalizzato in [0, 1].
Anche per funzioni definite in intervalli illimitati si può parlare di integrale generalizzato.
Definizione:
Sia f : [a, +∞[→ R integrabile in senso generalizzato (oppure alla Riemann) in ciascun intervallo
del tipo [a, x], con x ∈ R, x > a. Diremo che f è Integrabile in Senso Generalizzato in [a,+∞ [ se
esiste in R il limite
.
26 di 65
Sia f : ]−∞, b]→ R integrabile in senso generalizzato (oppure alla Riemann) in ciascuno degli
intervalli del tipo [x, b], con x ∈ R, x < b. Diremo che f è Integrabile in Senso Generalizzato in
]−∞,b] se esiste in R il limite
.
Proposizione (senza dimostrazione): Sia f : [a, +∞[→ R [f : ]−∞, b]→ R] integrabile in senso
generalizzato, e supponiamo che esiste in
il limite
.
Tesi: Allora dev’essere necessariamente l = 0 (N.B.: può comunque capitare che il limite l non
esista in
e che f sia integrabile in senso generalizzato in [a, +∞[ o ] −∞, b]!).
Studiamo ora fα : [1, +∞ [→ R, definita ponendo
α , fα è integrabile in senso generalizzato.
Se α
(α > 0), e vediamo per quali valori di
1, si ha:
Se α > 1, risulta:
.
R, in quanto 1 − α < 0 e
Se 0 < α < 1, si ha:
1− α è stavolta positivo.
Per α = 1, si ha:
.
, in quanto x tende a +∞, e l’esponente
, da cui
.
Quindi la funzione : per α > 1, è integrabile in senso generalizzato in [1,+∞[, mentre per 0 <α <
1 e per α = 1 non è integrabile in senso generalizzato in [1, +∞[ (comportamento analogo a quello
della serie armonica generalizzata).
Esercizio:
Vedere se la seguente funzione è integrabile in senso generalizzato in [2, +∞[ e se lo è in [0,1/2].
Svolgimento:
Innanzi tutto, si ha:
.
Quindi:
.
Quindi, in [2, +∞[, la nostra f non è integrabile in senso generalizzato. Vediamo ora in [0,
= numero reale
Dunque, f non è integrabile in senso generalizzato neanche in [0,
]. Si ha:
].
27 di 65
Esercizio:
Calcolare: I =
Si ha: I =
.
.
Calcoliamo dapprima l’integrale indefinito
, utilizzando il seguente “trucco”: quando al
denominatore c’è un polinomio di quarto grado con potenze pari, porre
. Si ottiene:
, quindi
.
Pertanto
I=
.
Formula di Taylor
La formula di Taylor serve ad approssimare (con una buona approssimazione) una funzione
mediante dei polinomi.
Iniziamo con alcune considerazioni riguardanti direttamente i polinomi: per esempio, per
semplicità, sia P :[x0 − k, x0 + k] → R un polinomio di grado 4.
Si ha: P(x0 + h) = a0 + a1h + a2h2 + a3h3 + a4h4 ∀ h ∈ [−k, k].
Calcoliamo ora i coefficienti a0, a1, a2, a3, a4.
Per h = 0, abbiamo
P(x0) = P(x0 + 0) = a0
P'(x0 + h) = a1 + 2a2h + 3a3h2 + 4a4h3
P'(x0) = P'(x0 + 0) = a1
P''(x0 + h) = 2a2 + 6a3h + 12a4h2
a0 = P(x0)
a1 = P'(x0)
P''(x0) = P''(x0 + 0) = 2a2
P'''(x0 + h) = 6a3 + 24a4h
P'''(x0) = 6a3
P'v(x0 + h) = 24a4
Se P è un polinomio di 4° grado, allora
L’idea è quindi quella di approssimare una funzione f molto “regolare” con il polinomio
.
28 di 65
Formula di Taylor con resto di Peano
Teorema (senza dimostrazione):
Sia f : [x0 − k, x0 + k]→ R una funzione avente derivata di ordine n in [x0 − k, x0 + k] e che ammette
derivata di ordine n + 1 nel punto x0. Allora, ∀ h ∈ [−k,k], è:
, con
.
Vediamo da vicino il significato di questa formula per n = 0: questa formula ci fornisce, per n = 0,
sostanzialmente una proprietà equivalente alla derivabilità.
Riprendiamo la definizione di derivata.
Ricordiamo che f è derivabile in x0 se ∃ in R il
Dalla definizione di derivata segue che:
ove
.
(∀ h appartenente ad un opportuno intorno
di x0), ossia:
, cioè
ecco la formula di Taylor per n = 0;
se vogliamo la possiamo prendere come definizione di differenziabilità: cioè si dice che f è
differenziabile in x0 se ∃ un intorno U di x0 e se ∃ un numero reale L tale che, ∀ h ∈ U, si ha:
(*)
,
ove : U → R è una funzione tale che
, cioè un infinitesimo. Si può provare che una
funzione è differenziabile in x0 se e solo se è derivabile in x0, ed in tal caso L = f '(x0).
La quantità Lh, cioè f '(x0) ⋅ h, si chiama Differenziale di f in x0.
La formula (*) esprime anche il fatto che f è “ben approssimata” dalla funzione lineare (cioè: dal
polinomio di grado 1) in h: f (x0) + Lh, perché quello che resta è
, cioè un infinitesimo
di ordine superiore rispetto ad h, ossia una quantità “trascurabile” (questo è tra l’altro lo spirito della
formula di Taylor di ordine n, per ogni n ∈ IN: cioè la “buona” (in questo senso) approssimazione
di f con un polinomio di grado n).
Possiamo dunque scrivere:
df := f '(x0) ⋅ h = differenziale di f in x0
differenziale
29 di 65
L’equazione della retta tangente ( ) alla curva y = f (x) nel punto P ≡ (x0, f (x0)) è
y - f (x0) = f '(x0) (x − x0), cioè y = f (x0) + f '(x0) (x − x0). (‡)
S è quel punto la cui ordinata y si calcola con la formula (‡) nel caso in cui al posto di x ci si mette
x0 + h; ossia l’ordinata di S è: f (x0) + f '(x0) (x − x0) = f (x0) + f '(x0) ⋅ h. Quindi
= ordinata di
S−ordinata di R = f (x0) + f '(x0) ⋅ h − f (x0) = f '(x0) ⋅ h. L’errore è
, che è h ⋅ ε( x0, h), che è
“trascurabile” (h è molto vicino ad x0; quindi le proporzioni del disegno nella figura di sopra non
vanno considerate…).
Teorema (senza dimostrazione):
Sia f : [x0 − k, x0 + k]→ R avente derivate fino all’ordine n + 1 in [x0 − k, x0 + k].
Sussiste la Formula di Taylor con resto di Lagrange: ∀ h ∈ [−k,k] si ha
, ove ϑ è un opportuno numero
appartenente all’intervallo aperto ]0, 1[.
Definizione:
Si dice che f : [x0 − k, x0 + k]→ R è Sviluppabile in serie di Taylor in [x0 − k, x0 + k] se ∀
h ∈ [−k,k] si ha:
con le convenzioni: f (0)(x0) = f (x0) e 00 = 1 (quest’ultima convenzione vale solo nelle serie: 00, nei
limiti, è una forma indeterminata).
Notiamo che una condizione necessaria affinché f sia sviluppabile in serie di Taylor è che f ammetta
derivate di qualsivoglia ordine: questa condizione, però, non è sufficiente: infatti esistono funzioni
che ammettono derivate di ordine n ∀ n ∈ IN e che non sono sviluppabili in serie di Taylor.
Sussistono comunque le seguenti due condizioni sufficienti (senza dimostrazione):
Teorema (senza dimostrazione):
Se f : [x0 − k, x0 + k]→ R ammette derivate di qualsivoglia ordine ed è tale che esiste M > 0 tale che,
∀ n ∈ IN, ∀ x ∈ [x0 − k, x0 + k], si abbia
,
allora f è sviluppabile in serie di Taylor in [x0 − k, x0 + k].
Teorema (senza dimostrazione):
Se f : [x0 − k, x0 + k]→ R ammette derivate di qualsivoglia ordine ed è tale che ∃ L > 0 tale che, ∀ n
∈ IN, ∀ x ∈ [x0 − k, x0 + k], si abbia
,
allora f è sviluppabile in serie di Taylor in [x0 − k, x0 + k].
Per esempio, sin x è sviluppabile in serie di Taylor in [−k, k] ∀ k ∈ R+, con L = 1 (per es.); infatti:
|sin(0)(x)| = |sin x| 1, |sin'(x)| = |cos x| 1, |sin''(x)| = |−sin x| 1, |sin'''(x)| = |−cos x| 1∀ x ∈ R, e
via dicendo… Quindi, in virtù dell’arbitrarietà di k ∈ R+, si ottiene che la funzione sin x è
sviluppabile in serie di Taylor in tutto R. Una proprietà analoga vale per la funzione coseno. Anche
la funzione esponenziale ex è sviluppabile in serie di Taylor in tutto R. Sussistono le seguenti
formule (senza dimostrazione) (∀ x ∈ R):
30 di 65
Si parte dal punto iniziale x0 = 0.
(N.B.: Gli sviluppi in serie e le formule di Taylor, quando x0 = 0, si chiamano -in letteraturarispettivamente sviluppi in serie e formule di MCLAURIN)
Per −1 < x < 1 sussiste anche questo sviluppo in serie (SERIE BINOMIALE):
(ove
Inoltre, per −1 < x
)
1, si ha anche lo sviluppo in serie logaritmica:
Dallo sviluppo in serie dell’arcotangente si ottiene, per x = 1:
Osservazione: Si può dare una sorta di “definizione alternativa” di ex:
.
Introduzione ai numeri complessi
Numeri complessi: z = x + iy = ρ (cos ϑ + i sin ϑ).
, o i logaritmi
Nel campo dei numeri reali, è impossibile eseguire certe operazioni, per esempio
di numeri negativi. Si deve quindi uscire dall’insieme R e introdurre un nuovo insieme (insieme dei
numeri complessi C). In questo contesto, non daremo la definizione rigorosa dei numeri complessi.
Diremo solamente, in modo semplicistico:
Porremo i2 = −1 (i sarà un numero non appartenente a R) e imporremo che valgano tutte le regole
dell’algebra analoghe a quelle che valgono in R. I numeri complessi saranno quindi quei numeri z
della forma z = a + ib, con a, b ∈ R.
Il numero a si chiama la Parte Reale del numero complesso z, mentre il numero b si chiama
Parte Immaginaria del numero complesso z.
31 di 65
Se z = a + ib, chiameremo coniugato di z (e la indicheremo con ) il numero complesso a − ib.
(Invece di a ± ib, si può scrivere a ± bi). Adesso facciamo qualche operazione con i numeri
complessi:
(2 − 3i) + (4 − 5i) = 6 − 8i
(3 + i) (4 − 2i) = 12 − 6i + 4i − 2i2 = 12 + 2 − 2i = 14− 2i
y = Asse immaginario
(Supponiamo P 0)
P = (a,b) = a+ib
ϕ
x = Asse reale
Sia
: ρ = modulo di z, e lo si indica con | z |.
Fissato sul piano, come verso positivo delle rotazioni, quello antiorario e indicata con ϕ la misura
(in radianti) del minimo angolo di cui si deve ruotare l’asse intorno all’origine 0 e nel verso
positivo, per disporsi nella retta per 0 e P, orientata da 0 verso P, si chiama Argomento di a + ib uno
qualunque dei numeri reali
ϑ = ϕ + 2kπ,
con k ∈ Z = {0,+1,−1,+2,−2,+3,−3,…}.
Si ha: a = ρ cos ϑ, b = ρ sin ϑ, e quindi a + ib = ρ (cos ϑ + i sin ϑ). Si può anche dimostrare la
seguente Formula di Eulero:
ϑ
ei = cos ϑ + i sin ϑ
∀ϑ∈R
z
(N.B.: Qui e , con z ∈ C, lo si definisce analogamente a come lo era stato “definito” nel campo dei
numeri reali, cioè:
come somma di serie).
ϑ
La forma z = ρ (cos ϑ + i sin ϑ) oppure z = ρei si chiama Rappresentazione Trigonometrica del
numero complesso z.
Dato un numero complesso z = a + ib, il suo modulo, come detto, è dato da
z = 0) e, se z è diverso da zero, il suo argomento ϑ è determinato dalle equazioni
(ρ = 0 se
,
(Bisogna stare attenti in quale quadrante del piano cartesiano ci troviamo).
Potenze e radici nel campo complesso
Sia z
0, e siano ρ e ϑ rispettivamente il modulo e l’argomento di z. Si ha
.
Definiamo ora la radice n-esima di un numero complesso z, con n ∈ IN.
Chiamiamo radice n-esima di z ogni numero complesso x che soddisfa l’equazione
xn = z .
Se z = 0, allora l’unica soluzione dell’uguaglianza è ovviamente x = 0.
Sia z
iϑ
0, z = ρe . Se x = re
rn. ein = ρ e
iϑ
i
è un numero complesso che soddisfa l’uguaglianza, si deve avere
e da ciò segue rn = ρ ,
.
32 di 65
Dalla prima relazione si ha:
, e dalla seconda si ha:
,
k ∈ Z.
Si può dimostrare che le radici n-esime del numero complesso z sono n, e quindi si ha:
,
k = 0, 1, …, n − 1.
Esempio:
Calcolare le radici quarte di 1. n = 4
.
Quindi, nel campo dei numeri complessi, si ha che le radici quarte di 1 sono i
quattro numeri 1, i, −1, −i.
Logaritmi nel campo complesso
Dato un numero complesso z 0 di modulo ρ e argomento ϑ, consideriamo nel campo complesso
l’equazione nella variabile x
(*) ex = z .
Prima di questo, facciamo vedere che la funzione esponenziale ez è periodica di periodo 2π i.
Infatti si ha:
,
e quindi
∀ z ∈ C.
Poiché, scrivendo z nella forma trigonometrica, è
, ne segue che una soluzione
dell’equazione (*) è
.
Tenendo conto che la funzione esponenziale, nel campo dei numeri complessi, è periodica di
periodo 2πi, si ha che tutte le soluzioni della (*) sono date da
, k ∈ Z.
Allora, dato z 0, chiameremo logaritmo di z (in base e), e scriveremo log z, ogni soluzione
dell’equazione (*).
Ogni numero complesso z 0 ammette quindi un’infinità numerabile di logaritmi in base e, che
sono dati da: log z =
, k ∈ Z.
(cioè quel logaritmo che corrisponde
Si chiamerà Logaritmo Principale di z la quantità
al numero intero 0).
Con abuso di notazione: Il logaritmo di un numero complesso z 0, nella base complessa y 0, si
definisce ponendo
(dove ha senso).
y
L’estensione al campo complesso della nozione di logaritmo permette di definire la potenza z con
z ed y complessi e z 0.
Si pone:
,
ove log z indica uno qualunque degli infiniti logaritmi di z in base e.
33 di 65
Esempio:
−5: ρ = 5, ϑ = π
,
k ∈ Z.
Quindi esistono i logaritmi dei numeri reali negativi, ma solo nel campo dei numeri complessi.
Nel campo dei numeri reali, non esistono logaritmi dei numeri reali negativi.
Il logaritmo di 0 non esiste né nel campo dei numeri reali né in quello dei numeri complessi.
Funzioni di Due Variabili
Sia IR2 il piano cartesiano.
Fissato un punto (x0, y0) ∈ IR2, si chiama Intorno di (x0, y0) un qualsiasi
insieme U che contiene un piccolo cerchio, o un quadratino, o un
rettangolino, o un piccolo rombo centrato in (x0, y0).
Nella figura, U1 è intorno di (x0, y0) mentre U2 non è
intorno di (x0, y0). Un concetto analogo di intorno si
può estendere nello spazio euclideo tridimensionale
IR3: ai piccoli cerchi corrispondono le sferette, ai
quadratini i cubetti, ai rettangolini i piccoli
parallelepipedi, etc.
Definizione:
Un insieme A ⊂ IR2 si dice APERTO se è vuoto oppure se, contenendo un punto (x0, y0), contiene
un intorno U centrato in (x0, y0).
Aperto
Non aperto
Un insieme C ⊂ IR2 si dice CHIUSO se il suo complementare è un aperto.
Dato A ⊂ IR2, A aperto non vuoto (per semplicità), considereremo le funzioni di due variabili
f : A → R.
Una funzione di due variabili è una legge che a due numeri reali x, y, tali che (x, y) ∈ A (cioè a ogni
coppia di numeri reali (x, y) tali che (x, y) ∈ A), fa corrispondere uno e un solo valore reale, che
chiameremo f (x, y).
Esempio:
x+ y
=e e
f: IR2 → IR2, f ( x, y ) = e
Data una funzione di due variabili x ed y, si possono considerare le derivate parziali rispetto alla x e
rispetto alla y. La derivata parziale rispetto alla x [risp. y] la si fa derivando rispetto alla x [risp. y] e
considerando la variabile y [risp. x] come se fosse una costante. Per esempio, se
x
y
f ( x, y ) = e x + y = e x e y , allora la derivata parziale rispetto ad x è D(e x )e y = e x e y .
Se
, allora la sua derivata parziale rispetto ad x è 2y2, perché è
.
34 di 65
Il simbolo Dx può generare confusione, perché si sottintende che la derivata che compare
dev’essere fatta rispetto alla x.
Per ovviare a ciò, in letteratura la derivata parziale rispetto a x si indica col simbolo
col simbolo
. Quindi
oppure
.
Inoltre,
.
Anche per le funzioni di due variabili si possono introdurre i concetti di limite e di continuità.
Diremo che
con l reale oppure +∞ o −∞, se per ogni intorno ϑ di l esiste un
intorno U di (x0, y0) tale che ∀ (x, y) appartenente ad U ∩ A \ {(x0, y0)} (qui A è l’insieme di
definizione della nostra f ) si ha f (x, y) ∈ ϑ.
(N.B.: Si suppone sempre che A sia un aperto non vuoto di IR2).
Diremo che f : A → R è continua in (x0, y0) ∈ A se
.
Diremo che f : A → R è continua in A se f è continua in (x0, y0) per ogni (x0, y0) ∈ A.
Osservazione Importante:
Mentre una funzione di una variabile derivabile in x0 è continua in x0, non è detto invece che una
funzione di due variabili che ammetta derivate parziali in (x0, y0) sia continua in (x0, y0).
Il concetto di continuità è un concetto “globale”, cioè “che riguarda un intorno U ⊂ IR2 nella sua
globalità”.
Quello che invece in IR2 corrisponde veramente alla derivabilità è la differenziabilità, che ora
introduciamo.
Definizione:
Sia A ⊂ IR2 un aperto non vuoto, e sia
A. Diremo che f : A → R è differenziabile in
se esistono due numeri reali P, Q ed una funzione ε: IR2 → R, con
risulti
, in modo che
comunque si prendano h, k con
A.
Notiamo che, se f è differenziabile in
, allora f è continua in
; inoltre, se f è
differenziabile in
, allora f è derivabile parzialmente in
, e si ha:
,
,
ove P e Q sono come nella definizione di differenziabilità data in precedenza.
Si può dimostrare anche che, se f : A → R, con A ⊂ IR2, ammette continue le derivate parziali fx, fy
in A, allora f è differenziabile in A.
Minimi e Massimi Relativi
Sia data una funzione f : A → R, con A ⊂ IR2, A aperto non vuoto. Un punto
di A si dice
tale che per ogni
punto di minimo relativo [massimo relativo] per f se esiste un intorno U di
(x, y) ∈ U ∩ A risulta f (x, y) f
[f (x, y) f
]. In tal caso il valore f
si dice un
minimo [massimo] relativo o locale per f .
Se poi risulta f
f (x, y) [f
f (x, y)] ∀ (x, y) ∈ A, allora il punto
si dirà un punto
di minimo assoluto [massimo assoluto], e il valore f
si dirà il minimo assoluto
[massimo assoluto] di f .
35 di 65
Si può dimostrare (ma noi non lo faremo) che (essendo A aperto non vuoto) i punti di minimo (o di
massimo) relativo che sono interni ad A e nei quali f è derivabile parzialmente, vanno ricercati fra le
soluzioni del sistema
.
Le soluzioni di tale sistema si chiamano “punti critici” o “punti stazionari”.
Tuttavia non tutti i punti critici sono punti di massimo o di minimo relativo.
Quindi siamo di fronte a una condizione necessaria (ma non sufficiente) per avere punti di
massimo e/o minimo relativo. Vediamo ora qualche condizione sufficiente, che permetta di
introdurre qualche metodo “pratico” per lo studio dei massimi e minimi relativi per le funzioni di
due variabili.
A questo scopo introduciamo il concetto di derivata parziale seconda: lo facciamo
direttamente con degli esempi.
1)
è “la derivata parziale rispetto a x della derivata parziale di f rispetto a x”
per esempio, se
2)
.
è “la derivata parziale rispetto a y della derivata parziale di f rispetto a y”.
per esempio, se
3)
, si ha
, si ha
.
è la derivata parziale rispetto ad y della derivata parziale di f rispetto ad x.
per esempio,
4) Analogamente,
, si ha
.
è la derivata parziale rispetto ad x della derivata parziale di f rispetto ad y.
per esempio, se
, si ha
.
Introduciamo ora la matrice HESSIANA (e l’HESSIANO) della f nel punto
La matrice Hessiana di f nel punto
.
è la matrice
(fxx è un simbolo più sintetico per indicare la quantità
, e via dicendo…), mentre il suo
determinante lo chiameremo hessiano di f nel punto
, e lo denoteremo ancora con il simbolo
(si capirà dal contesto se si parla della matrice o del determinante).
Sussiste il seguente teorema (senza dimostrazione).
36 di 65
Teorema (senza dimostrazione):
Sia f : A → R, con A aperto non vuoto, A ⊂ IR2, e supponiamo che esista un intorno U di
su
cui f sia continua insieme alle sue derivate parziali prime e seconde.
Supponiamo infine che
In tal caso si ha:
1) Se
.
et
, allora
è un punto di minimo relativo;
2) se
et
, allora
è un punto di massimo relativo;
3) se
, allora
non è né un punto di max né di min. relativo (e in questo caso si
dice che il punto
è un punto sella);
4) se
, allora non si può dire nulla ed occorre fare altre indagini.
Esempi:
R con
1) Sia f : IR2
.
Sappiamo già che
,
Il sistema “dei punti critici”
,
,
,
.
fornisce come unica soluzione il punto (0, 0) e si ha
.
Quindi
,
, e perciò il punto (0, 0) è di
minimo relativo, come si vedeva facilmente anche “a intuito”.
2) Sia f : IR2
R con
.
Si ha:
,
,
,
,
.
Quindi
.
Il punto (0,0) non è né un punto di minimo né un punto di massimo relativo, e quindi in questo
caso si dice che il punto (0, 0) è un punto sella.
Teorema Fondamentale dell’algebra (senza dimostrazione):
Un’equazione algebrica P(x) = 0, ove P è un polinomio di grado n, ammette nel campo complesso
esattamente n radici.
Esempi:
L’equazione x4 – 1 = 0 cioè x4 = 1, nel campo dei numeri complessi ammette
4 radici, che sono date dai numeri 1, –1, i, –i, come abbiamo già
precedentemente visto.
Nel campo dei numeri reali, quest’equazione ammette solo 2 radici (1 e –1).
Notiamo anche che, se un’equazione del tipo P(x) = 0, con P polinomio,
ammette una radice complessa a + ib, allora ammetterà anche la sua
coniugata a – ib.
37 di 65
Da ciò si ritrova il risultato che un polinomio di grado dispari ammette
almeno una radice reale (Essendo infatti un polinomio di grado dispari,
quando si fanno le “coppie” tra le varie radici, e dovendo prendere
sempre le coniugate, una rimarrà “spaiata”. Allora questa radice
dev’essere un numero tale che il suo coniugato coincida con se stesso:
questa condizione si verifica se e solo se il numero è reale).
(x,y,f(x,y))
Significato geometrico della differenziabilità di una funzione
di due variabili f nel punto
: vuol dire, in sostanza, che
esiste (ed è unico) il piano tangente alla superficie z = f (x, y)
nel punto
.
z =f (x,y)
Autovalori e Autovettori
di una matrice A 2 x 2 oppure 3 x 3
a11 a12 a13 
 a11 a12 
oppure A = a 21 a 22 a 23 
A=



 a 21 a 22 
a 31 a32 a33 
 x1 
x =   nel caso bidimensionale, oppure
 x2 
 x1 
x =  x 2  nel caso tridimensionale.
 x3 
a11 x1 a12 x 2 a13 x 3 
Ax = “prodotto righe per colonne” A = a 21 x1a 22 x 2 a 23 x3  nel caso tridimensionale,


a 31 x1a32 x 2a33 x3 
a x a x 
oppure A =  11 1 12 2  nel caso bidimensionale.
a 21 x1a 22 x 2 
λx1 
λx1 
 
(∀ λ ∈ C)
λx =   oppure λx = λx 2 
λx 2 
λx3 
λa11λ a12 
λA = 
 nel caso 2 x 2, oppure
λa 21 λa 22 
λa11λa12 λa13 


λA = λa 21λ a 22 λa 23  nel caso 3 x 3 (∀ λ ∈ C).
λa31 λa32 λa 33 
38 di 65
Definizione: Data una matrice A 2 x 2 o 3 x 3, si chiama autovalore λ ∈ C ogni soluzione
dell’equazione algebrica det(A – λI) = 0, ove:
1 0 0
1 0
oppure I = 0 1 0
I=

0 1
0 0 1
λ 0 0 
λ 0 
oppure λI =  0 λ 0 
λI = 

0 λ 
 0 0 λ 
a11 − λ
a12 
oppure A − λI =  a 21


a 22 − λ 
 a31
det è il determinante.
a11 − λ
A − λI = 
 a 21
a12
a 22 − λ
a32
a13 
a 23 
a 33 − λ 
Definizione: Data una matrice A ed un suo autovalore λ, si chiama autovettore (associato
all’autovalore λ) ogni vettore x, diverso dal vettore nullo, tale che Ax = λx.
Stabiliamo ora un “collegamento” tra la formula Ax = λx, x ≠ 0 e det(A – λI) = 0.
Per semplicità consideriamo il caso 2 x 2: analogamente si procede nel caso 3 x 3.
Ax = λx si può esprimere, in virtù delle considerazioni precedenti, nel modo seguente:
 a11 x1 + a12 x 2  λx1 
 a x + a x  = λx  , cioè
 21 1
22 2 
 2
,
.
Si tratta di un sistema omogeneo di due equazioni e due incognite, che sono x1 ed x2. Esso ammette
 x  0
sempre la soluzione banale, cioè  1  =   . Condizione necessaria e sufficiente affinché il nostro
 x 2  0
sistema abbia soluzioni diverse da quella banale è che
a12 
a11 − λ
det 
=0
a 22 − λ 
 a 21
(questa è una proprietà che viene dalla teoria dei sistemi lineari, e che qui diamo per scontata), cioè
det(A – λI) = 0.
Definizione di matrice simmetrica:
a a 
Si dice che A =  11 12  è simmetrica se a12 = a21.
 a 21 a 22 
a11 a12 a13 
Si dice che A = a 21 a 22 a 23  è simmetrica se a12 = a21, a13 = a31, a23 = a32.


a 31 a32 a33 
Teorema (senza dimostrazione):
Se A è simmetrica, allora i suoi autovalori sono tutti quanti reali.
39 di 65
Esercizio:
2 0 
Calcolare gli autovalori e gli autovettori della matrice A = 
.
 0 − 2
Autovalori: det(A – λI) = 0, cioè
, ossia
(2 – λ)⋅(–2 – λ) = 0, cioè (2 – λ)⋅(2 + λ) = 0
λ = 2, λ = –2 sono i nostri autovalori (com’era facilmente “prevedibile”).
Autovettori: In corrispondenza all’autovalore λ = 2
 2 0   x1  2 x1 
Ax = 2x
0 − 2  x  = 2 x 

 2   2 
I vettori (x1, 0), con x1 ∈ R\{0} (perché il vettore (0, 0), cioè il vettore identicamente nullo, è
da escludere), costituiscono gli autovettori associati all’autovalore λ = 2.
Ora, in corrispondenza all’autovalore λ = –2, si ha:
 2 0   x1  − 2 x1 
Ax = –2x
0 − 2  x  = − 2 x 
2

 2  
I vettori (0, x2), con x2 ∈ R\{0}, costituiscono gli autovettori associati all’autovalore λ = –2.
Osservazione: Se f funzione di più variabili ha derivate parziali prime e seconde continue, allora
la matrice hessiana è simmetrica (senza dimostrazione), e quindi essa ammette autovalori reali
Test del Hessiano:
(Formulazione con gli autovalori: vale sia per funzioni di due che per funzioni di tre variabili)
(Partiamo dai punti critici (x0, y0))
Se la matrice hessiana H = H(x0, y0) è definita positiva, cioè ha autovalori tutti positivi, allora il
punto critico o stazionario (x0, y0) (ossia tale che fx(x0, y0) = 0 = fy(x0, y0)) è un punto di minimo
relativo.
Se la matrice hessiana H è definita negativa, cioè ha autovalori tutti quanti negativi, allora il punto
critico (x0, y0) è un punto di massimo relativo. Se H ha autovalori sia positivi che negativi, allora
(x0, y0) è un punto sella (cioè né di massimo né di minimo relativo). Se H ha l’autovalore nullo,
allora non si può dire nulla.
Esempio:
f (x, y) = x2 – y2
Condizione necessaria ma non sufficiente per avere punti di massimo e/o di minimo relativo è
l’annullamento del gradiente, che nel nostro caso si scrive
Il punto (0, 0), cioè l’origine, è un “candidato”.
Notiamo che fxx = 2, fyy = – 2, fxy = fyx = 0.
 f xx f xy  2 0 
H ( x, y ) = 
=

 f yx f yy  0 − 2
40 di 65
ha autovalori 2 e –2 (l’abbiamo visto prima), che sono di segno variabile.
Si tratta dunque di un punto SELLA.
Osservazione: In questo corso, mentre il test dell’hessiano per funzioni di due variabili è
formulato sia con sia senza gli autovalori (e quindi lo studente può scegliere), per le funzioni di 3
variabili il test dell’hessiano è presentato solamente con gli autovalori e quindi bisogna
necessariamente conoscere gli autovalori. Esistono in letteratura anche versioni del test
dell’hessiano per funzioni di tre variabili senza ricorrere alla teoria degli autovalori, ma ci sembrano
troppo complicate – a nostro avviso – e quindi esulano dallo spirito del corso.
Esercizio:
Determinare gli eventuali punti di massimo e minimo relativo della funzione
f (x, y, z) = x2 + y2 + z2 + xz + yz + 2x – 2y – 4z .
Imponiamo la condizione necessaria dell’annullamento del gradiente.
In corrispondenza di z = 4 si avrà: x = –3, y = –1.
Quindi l’unico punto critico è il punto P = (–3, –1, 4).
Si ha inoltre:
e quindi
0
1 
2 0 1 
2 − λ



H ( x, y, z ) = 0 2 1  pertanto H − λI =  0
2−λ
1 
1 1 2
 1
1
2 − λ 
Siamo nel caso di funzioni a 3 variabili, e dunque dobbiamo calcolare gli autovalori della matrice
hessiana. Si deve avere:
0
1 
2 − λ

0 = det( H − λI ) = det  0
2−λ
1  = ...
 1
1
2 − λ 
Applichiamo la regola di Sarrus:
… = (2 – λ) ⋅ (2 – λ) ⋅ (2 – λ) + 0 + 0 – 0 – (2 – λ) ⋅ 1 – (2 – λ) ⋅ 1 = (2 – λ) ⋅ [(2 – λ)2 – 1 – 1] =
= (2 – λ) ⋅ (λ2 – 4λ + 2).
λ = 2: autovalore positivo
λ2 – 4λ + 2: poiché H – λ I è simmetrica, allora gli autovalori sono tutti quanti reali.
Il trinomio λ2 – 4λ + 2 presenta due “variazioni” (cioè due cambiamenti di segno quando si
considerano i suoi coefficienti 1, –4, +2), e quindi ci sono altri due autovalori positivi. Non c’è
bisogno di fare i calcoli! Gli autovalori sono tutti e tre positivi, e dunque (–3, –1, 4) è un punto di
minimo relativo.
Lo studente può affrontare ora i relativi esercizi dei compiti.
41 di 65
Integrali Doppi
In questo corso affronteremo gli integrali doppi solo come poco più che un cenno, e soprattutto da
un punto di vista “pratico”, riducendo cioè al minimo indispensabile i richiami teorici.
Siano α, β : [a, b]→ R due funzioni definite nell’intervallo chiuso e limitato [a, b] e ivi continue,
tali che α(x) < β(x) nei punti interni di [a, b]. L’insieme D dei punti del piano cartesiano IR2 le cui
coordinate cartesiane soddisfano alle condizioni:
a x b,
α(x) y β(x),
si chiama dominio normale rispetto all’ asse x.
Se f : D → R è una funzione di due variabili, f = f (x, y),
continua in D, allora l’integrale doppio esteso a D di f lo si può
definire nel seguente modo (“formula di riduzione”):
.
Se invece D è un dominio normale rispetto all’asse y, cioè è del
tipo D = {(x, y) ∈ IR2: c y d, γ(y) x δ(y)},
ove γ, δ :[c, d]→ R sono due funzioni continue con γ(y) < δ(y)
nei punti interni di [c, d], allora l’integrale doppio esteso a
D di f lo si può definire nel seguente modo:
x= (y)
x= (y)
.
Osservazione: Se D è normale sia rispetto all’asse x che rispetto all’asse y, allora si può vedere
che le due definizioni di integrale doppio sono equivalenti.
Le formule or ora viste possono essere utilizzate anche quando il dominio D, pur non essendo
normale rispetto a nessuno dei due assi, è decomponibile nell’unione di n domini normali a due a
due privi di punti interni in comune (In tal caso si fa la somma degli integrali relativamente ai
singoli domini normali).
Esercizio:
Calcolare l’integrale doppio:
,
ove D è il triangolo che ha per vertici i punti O = (0.0), A =
(1,0), B = (0,1).
Consideriamo D come un dominio normale rispetto all’asse x.
D = {(x, y) ∈ IR2: 0 x 1, 0 y 1 – x}. Pertanto si avrà:
(facendo l’integrale rispetto a dy, abbiamo considerato la x
come se fosse una costante…)
.
Pertanto il risultato è
.
42 di 65
Esercizio:
Calcolare l’integrale doppio:
I :=
,
ove D è il quadrato avente come vertici i punti (0,0), (0,1), (1,0), (1,1).
Soluzione: Si ha: D = {(x, y): 0 x 1, 0 y 1}.
Consideriamo il quadrato D come un dominio normale rispetto all’asse y. È:
I :=
Consideriamo la quantità
. Stiamo facendo l’integrale rispetto ad x, e quindi trattiamo x come
una variabile ed y come se fosse una costante.
Quindi, nella quantità
(rispetto a x). Pertanto
, possiamo dire che “il numeratore è la derivata del denominatore”
negative…)
(Qui, notiamo che le quantità x ed y sono non
, e quindi
I :=
.
Esercizio:
Calcolare il seguente integrale doppio:
I :=
ove D è il dominio del piano
delimitato dalle due parabole di equazioni:
,
.
Consideriamo D come un dominio normale rispetto all’asse x: sarà
I :=
D = {(x, y) ∈ IR2: 0 x 4,
y
}. Quindi
(Qui, per quanto riguarda l’espressione xy, considereremo y come variabile ed x come costante)
.
La teoria degli integrali doppi ha una significativa applicazione al calcolo di un integrale
particolarmente importante in Calcolo delle Probabilità e Statistica Matematica.
Richiamiamo le relazioni introdotte quando abbiamo studiato i numeri complessi:
x = ρ cos ϑ, y = ρ sin ϑ :
ρ e ϑ si chiamano anche Coordinate Polari.
Esercizio:
Dimostrare che l’integrale generalizzato
K:=
è uguale a
TRUCCO: Passiamo all’integrale doppio!
.
43 di 65
Studiamo l’integrale I:=
.
Si ha:
(Per la formula dell’integrale doppio…)
(IR2\{0} si scrive anche, in coordinate polari: D = {(x, y) ∈ IR2: 0 < ρ < +∞, 0 ϑ 2π}; inoltre,
fare l’integrale su IR2 o su IR2\{0} non cambia niente, si toglie solamente un punto; inoltre,
notiamo ora che da x = ρ cos ϑ, y = ρ sin ϑ segue x2 + y2= ρ2 cos2 ϑ + ρ2 sin2 ϑ =
=ρ2(cos2 ϑ + sin2 ϑ) = ρ2)
A questo punto, da dove sbuca questo ρ?
Il motivo del “ρ” in più è che si tratta di una formula del cambiamento di coordinate e bisogna
moltiplicare per lo “Jacobiano della trasformazione”, che in questo caso è per l’appunto ρ.
Lo jacobiano della trasformazione che esprime il cambiamento di coordinate
è il determinante della
matrice , cioè la quantità J= .
Che cosa sono le 4 quantità che compaiono nella matrice?
derivata di x rispetto a ρ, come se ϑ fosse costante.
Quindi
.
Analogamente:
;
;
.
2
2
Quindi J= cos ϑ ⋅ ρ cos ϑ + ρ sin ϑ ⋅ sin ϑ = ρ (cos ϑ + sin ϑ) = ρ.
Da questo diciamo che: lo jacobiano della nostra trasformazione “cambiamento di coordinate dalle
cartesiane alle polari” è effettivamente ρ.
Quindi
(infatti, adoperando la sostituzione w = ρ2, si ha
, quindi
; l’uguaglianza (1) segue quindi da ciò e dalla Formula
Fondamentale del Calcolo Integrale (FFCI), che vale anche per l’integrale generalizzato, purché si
intenda
)
. Pertanto
, e quindi
è una funzione pari (cioè tale che, ∀ x ∈ R,
K=
. Inoltre, poiché
), allora
come volevasi dimostrare.
44 di 65
Funzione Γ (Generalizzazione del Fattoriale)
Definiamo, ∀ t > 0,
Γ(t)
.
Notiamo che la funzione integranda è integrabile in senso generalizzato, e quindi Γ(t) è ben definita
∀ t > 0. Si ha:
Γ(1)
Γ (1) = 1
Si ha, ∀ t > 0: Γ(t + 1)
Γ(t)
.
Si ha: Γ(t + 1) = tΓ (t), ∀ t
Quindi, in particolare:
Γ(2) = 1 ⋅ Γ(1) = 1 ⋅ 1 = 1
Γ(3) = 2 ⋅ Γ(2) = 2 ⋅ 1 = 2
Γ(4) = 3 ⋅ Γ(3) = 3 ⋅ 2 = 6
Γ(5) = 4 ⋅ Γ(4) = 4 ⋅ 3 ⋅ 2 = 24 = 4!
Γ(6) = 5!
Γ(n) = (n – 1)!
∀ n ∈ IN, n 0
(Notiamo che, per definizione, 0! = 1)
Si ha:
Γ
(vedi pagine precedenti)
Si ha inoltre
Γ
=Γ
Γ
=Γ
=
=
Γ
Γ
=
=
Linee di Livello
Linee di livello k con -1 < k < 1 : sono le intersezioni della sfera con il
piano z = k , cioè le circonferenze di equazione
(ossia
)
(k in questo caso è un numero fissato, non una variabile)
Le circonferenze in figura rappresentano le equazioni di (tutte) le linee di
livello possibili e immaginabili associate alla sfera
(= superficie sferica)
rappresenta la circonferenza più grande.
Le linee di livello si possono costruire anche se si considera l’asse x o
l’asse y invece dell’asse z.
45 di 65
Equazioni Differenziali
Definizione: Si definisce Equazione Differenziale Ordinaria nelle funzioni incognite
y1(x), y2(x), … , yp(x) , con x ∈ I, I intervallo o semiretta di R, ogni equazione che lega la variabile
indipendente x, le funzioni incognite y1, y2, … , yp e le loro derivate, ossia:
,
cioè:
(1)
,
dove F è una funzione reale di n1 + … + np + 1 variabili.
Definizione: Si definisce Orfine di una data equazione differenziale, rispetto ad una delle
incognite yj, j = 1, … , p, l’ordine massimo delle derivate di yj che figura nell’equazione .
ordine globale = max (n1, n2, … , np)
Definizione: Si definisce Soluzione o Integrale dell’equazione differenziale ogni vettore di
componenti (y1, y2, … , yp), con le funzioni yj, j = 1, … , p definite e derivabili in I ⊆ R, I
opportuno intervallo, tali che introdotte nella (1) la rendono soddisfatta.
Per p = 1 l’equazione differenziale è:
F (x; y, y', … , y(n)) = 0 ed è di ordine n (rispetto alla variabile y).
(2)
L’equazione (2) è detta in Forma Normale o Canonica se può essere scritta nella forma:
y(n) = f (x; y(x), y'(x), … , y(n -1)(x)).
Problema 1:
Assegnati D ⊂ IR2 ed f : D→ R, determinare se esistono
I⊆R ,
y: I → R
derivabile in I (I intervallo), tali che:
1) (x, y(x)) ∈ D
∀ x ∈ I,
2) y'(x) = f (x, y(x))
∀ x ∈ I, dove
f : D→ R
è continua, con D ⊆ IR2 .
Questo problema può essere schematizzato con:
y' = f (x, y).
D
(E)
Problema 2 (Problema di Cauchy o del Valore Iniziale):
Assegnati D ed f come nel Problema 1, determinare se esistono I ⊆ R, I intervallo,
x0 ∈ I° (x0 interno ad I), y: I → R derivabile in I, tali che:
1) (x, y(x)) ∈ D
∀ x ∈ I,
2) y'(x) = f (x, y(x))
∀ x ∈ I,
3) y(x0) = y0,
dove f : D→ R,
D ⊆ IR2, f continua.
Può essere schematizzato con:
(E)
x0 ∈ I° .
46 di 65
Esempio:
1) Un esempio del Problema 1 è
y' = 1
al variare di c ∈ R.
2) Un esempio del Problema 2 è dato da:
.
Determiniamo il valore della costante c ∈ R in modo che sia verificata la
condizione y(1) = −1.
Calcoliamo il valore della costante:
.
Per cui la soluzione del problema è la seguente:
.
3) Consideriamo ancora il problema:
(E)
x0 ∈ I° .
Sussiste il seguente risultato:
Proposizione:
y soluzione di (E) ⇔
.
Vogliamo determinare delle condizioni, che ci permettano di studiare l’esistenza e l’unicità
delle eventuali soluzioni.
Sia D = R = [x0 – a, x0 + a] x [y0 – b, y0 + b] (con a, b ∈ R+) un rettangolo centrato nel punto
iniziale (x0, y0).
Teorema (senza dimostrazione):
f ∈ C(R) globalmente ⇒ (E) ammette (almeno una) soluzione.
continua
Definizione:
Sia f : D → R, con D ⊆ IR2, D = R rettangolo (come sopra). Si dice che
(x, y) → f (x, y)
f è Lipschitziana in D rispetto ad y uniformemente rispetto ad x se:
∃ k > 0 tale che: ∀ (x, y1), (x, y2) ∈ D ⇒ | f (x, y1) – f (x, y2) | k | y1 – y2 |.
(in breve f ∈ Lip(D))
Teorema (senza dimostrazione):
il problema (E) ammette un’unica soluzione
N.B. I due teoremi sono condizioni sufficienti ma non necessarie.
47 di 65
Teorema:
f:D→R
D ⊆ IR2
D = rettangolo
f è derivabile rispetto ad y in D
fy è limitata
⇒ f ∈ Lip(D).
Equazioni Differenziali a variabili separabili
y' = f (x, y) ⇒
f (x, y) = X(x) Y(y)
dove:
X: I → R
Y: J → R
I⊆R
J⊆R
I, J sono degli intervalli
D=IxJ
f:D→R
⇒
y' = X(x) Y(y)
è detta equazione differenziale a variabili separabili.
Per cui il problema di Cauchy sarà della forma:
Esercizio 1:
Dato il seguente problema di Cauchy determinare, se esistono, le eventuali soluzioni
è continua e localmente Lipschitziana, per cui il problema di Cauchy ammette un’unica soluzione.
⇒ f ∈ Lip(D)
Separando le variabili, si ottiene:
cioè:
.
Integrando ambo i membri:
arctg y = arctg x + arctg c.
Esplicitando la y, si ha:
y = tg (arctg x + arctg c).
48 di 65
Ricordando la formula:
∀ a, b ∈ R dove ha senso, si ottiene:
,
cioè
.
Imponendo la condizione iniziale determiniamo il valore della costante c :
2 (1 – c) = 1 + c ⇒ 2 – 2c = 1 + c ⇒ 1 = 3c ⇒ c =
.
Quindi la soluzione del problema di Cauchy è:
,
cioè
.
Esercizio 2:
Dato il seguente problema di Cauchy determinare, se esistono, le eventuali soluzioni.
.
è continua e Lipschitziana in un intorno del punto iniziale.
Essendo f (x, y) continua e localmente lipschitziana, allora il problema di Cauchy ammette un’unica
soluzione.
Separando le variabili:
Integrando ambo i membri:
possiamo togliere il modulo in quanto in un intorno del punto iniziale la y assume valori positivi
(N.B.: la costante c la considereremo dopo…).
49 di 65
Calcoliamo
A, B ∈ R da determinare
1 = A (x – 4) + Bx ⇒ 1 = Ax – 4A + Bx
1 = (A + B) x – 4A
cioè
.
Per cui sostituendo si ottiene:
.
Calcoliamo ora l’integrale:
(Siccome nella nostra condizione iniziale x0 = 5 > 4, allora abbiamo potuto scrivere log(x – 4)
anziché log|x – 4|). Ritornando all’equazione differenziale data, otteniamo:
.
Esplicitando y si ha:
Imponendo le condizioni iniziali passiamo a determinare il valore della costante c.
1 = 5c ⇒ c =
.
Per cui la soluzione del problema di Cauchy è:
.
50 di 65
Equazioni Lineari del primo ordine
Un’equazione differenziale è detta del equazione lineare del primo ordine se è della forma:
y' = a(x) y + b(x),
(*)
dove a(x) e b(x) sono due funzioni definite e continue in un intervallo I della retta reale.
Dunque il problema di Cauchy sarà della forma:
.
Essendo a(x) e b(x) funzioni continue ed y' una funzione continua, il problema ammette un’unica
soluzione.
L’equazione (*) è detta omogenea se b(x) = 0 (in tal caso essa risulta essere a variabili separabili);
non omogenea in caso contrario.
Vediamo come calcolare l’integrale generale.
y' = a(x) y + b(x)
y'–a(x) y = b(x)
Consideriamo:
y'1–a(x) y1 = 0 ,
(**)
dove con (**) abbiamo indicato l’equazione omogenea associata.
Tutte le equazioni differenziali lineari del primo ordine si risolvono nel seguente modo:
1° Passo) Si studia l’equazione omogenea associata e se ne determina l’integrale generale y1.
2° Passo) Si determina un integrale particolare (cioè una soluzione particolare )
dell’equazione differenziale data.
L’integrale generale dell’equazione data sarà y = y1 + (risultato senza dimostrazione)
separando le variabili otteniamo:
.
Integrando ambo i membri:
(senza restrizione si può supporre y1 > 0)
Quindi y1 è soluzione della (**).
Osserviamo che, se c è una costante reale, allora y1 non soddisfa l’equazione (*), dunque l’idea è
quella di modificare la costante, facendola dipendere dalla variabile x, in modo tale che la y1 sia
soluzione della (*). Tale metodo è noto come metodo della variazione delle costanti arbitrarie.
Sia
soluzione di (*).
Sostituendo si ottiene:
.
51 di 65
Integrando ambo i membri si ha:
L’integrale generale della (*) è dato da:
“Inglobando” c e c1, si ottiene:
con h costante reale.
Dato che l’integrale particolare è fissato (cioè è una cosa ben determinata, non una cosa che varia),
allora anche c1 è fissato, cioè possiamo (anzi: dobbiamo!) scegliere un solo valore di c1, per
esempio c1 = 0.
Quindi possiamo “inglobare” le due costanti; tra l’altro, essendo l’equazione del primo ordine, c’è
in realtà in generale UNA SOLA famiglia (e non due) di costanti arbitrarie.
A questo punto lo studente è invitato a “cimentarsi” sugli esercizi sulle equazioni differenziali del
primo ordine presi dai compiti degli anni precedenti, in particolare sulle equazioni differenziali a
variabili separabili e su quelle lineari.
Equazioni Differenziali del secondo ordine lineari a coefficienti
costanti
Sono del tipo:
y'' + a1y' + a2y = β(x),
ove β : I → R, con I intervallo o semiretta o tutto R, è una funzione continua.
Per risolvere questo tipo di equazioni differenziali, studiamo innanzi tutto l’equazione omogenea
associata y'' + a1y' + a2y = 0 .
A questa equazione associamo l’equazione algebrica λ2 + a1λ + a2 = 0 :
questa equazione si chiama Equazione caratteristica associata all’equazione differenziale
(omogenea).
Sussiste il seguente risultato, di cui non riportiamo la dimostrazione.
Si presentano i seguenti tre casi:
1) Se l’equazione caratteristica ammette due radici reali distinte, diciamo α1 ed α2, allora
l’integrale generale y1 dell’equazione omogenea sarà dato da
(con c1, c2 ∈ R).
2) Se l’equazione caratteristica ammette due radici reali coincidenti, diciamo α (con α abbiamo
indicato, ovviamente, il loro valore comune), allora l’integrale generale y1 dell’equazione
omogenea è
(con c1, c2 ∈ R).
3) Se l’equazione caratteristica non ammette nessuna radice reale, allora – in virtù di un noto
risultato che riguarda i numeri complessi, e del quale non diamo la dimostrazione – l’equazione
caratteristica ammette due radici complesse “coniugate”, cioè che sono rispettivamente del tipo
α1 = p + iq ed α2 = p – iq. In questo caso, l’integrale generale y1 dell’equazione omogenea è:
.
Una volta trovato l’integrale generale dell’equazione omogenea, si determinerà una soluzione
particolare (= integrale particolare) dell’equazione differenziale di partenza, applicando sempre una
versione del metodo della variazione delle costanti arbitrarie (che in questo caso sono c1 e c2).
52 di 65
Si pone rispettivamente nei 3 casi (nella ricerca di un integrale particolare
,
):
,
(ε)
, si impone che sia una soluzione dell’equazione
differenziale data calcolando da (ε) la quantità (x) e sostituendo, nell’equazione differenziale di
partenza, i valori di e di '.
Ci vorrà poi un particolare accorgimento (TRUCCO), e dopo si scriverà un sistema di due equazioni
e due incognite, che saranno c1'(x) e c2'(x).
Quindi da c1'(x) e c2'(x) si determineranno c1(x) e c2(x).
Dunque, lo spirito del metodo della variazione delle costanti arbitrarie è quello di far “variare” le
costanti c1 e c2 (che corrisponderebbero al caso β(x) = 0), facendole “diventare” funzioni della x, in
modo tale che sia una soluzione dell’equazione differenziale data.
(N.B.: L’integrale generale è, diciamo, l’insieme delle soluzioni)
Anche in queste equazioni, che sono lineari, l’integrale generale dell’equazione data è uguale
all’integrale generale dell’omogenea associata più un (qualsiasi) integrale particolare dell’equazione
di partenza.
Illustriamo l’operatività del metodo della variazione delle costanti arbitrarie con un esempio.
In questo esempio calcoleremo anche qualche integrale del tipo
,
che non era stata fatta nella parte riguardante il Calcolo degli integrali indefiniti.
, cosa
Esercizio 1:
Risolvere il seguente problema di Cauchy:
.
È un’equazione differenziale lineare del secondo ordine omogenea a coefficienti costanti: la sua
equazione caratteristica associata è:
λ2 + 1 = 0
λ = ±i
2
λ = –1
L’integrale generale dell’equazione data è:
y = c1 cos x + c2 sin x.
Imponendo la prima condizione iniziale, y(0) = 0, si ottiene: 0 = y(0) = c1 cos 0 + c2 sin 0 = c1 e
quindi c1 = 0. Pertanto y = c2 sin x, da cui y' = c2 cos x.
Poiché y'(x) = c2 cos x, allora y'(0) = c2 cos 0 = c2 .
Imponendo ora la seconda condizione iniziale y'(0) = 1, si ottiene 1 = y'(0) = c2, cioè c2 = 1, e quindi
y(x) = sin x è la soluzione del nostro problema, com’era facilmente prevedibile.
Esercizio 2:
Dato il problema
si chiede di:
a) risolvere il problema;
b) calcolare un integrale particolare dell’equazione y'' + 25 y = e7x con il metodo della
variazione delle costanti arbitrarie.
53 di 65
Soluzione:
Innanzi tutto consideriamo l’equazione caratteristica (∇) associata dell’equazione omogenea
associata
y'' + 25 y = 0 : essa è
(+)
2
λ + 25 = 0, da cui λ = ± 5i.
(∇)
Quindi, in virtù di noti risultati della teoria, l’integrale generale dell’equazione (+) è
y = c1 cos 5x + c2 sin 5x.
Si osservi che un integrale particolare dell’equazione data y'' + 25 y = e7x può essere calcolato
facilmente, senza bisogno di ricorrere al metodo della variazione delle costanti arbitrarie,
osservando che la derivata di eαx è α eαx ∀ α ∈ R e cercando quindi funzioni del tipo
y(x) = α e 7x con α ∈ R da determinare. Si deve avere: y'(x) = 7α e7x, y''(x) = 49α e7x, e7x = y'' + 25y
= 49α e7x + 25 α e7x = 74 α e7x, e quindi 74α = 1, cioè
integrale particolare dell’equazione differenziale data
(senza le due condizioni “iniziali”
. Quindi
,
è un
)
Come detto, l’integrale generale dell’equazione omogenea associata è y = c1 cos 5x + c2 sin 5x.
Cerchiamo un integrale particolare con il metodo della variazioni delle costanti arbitrarie, ossia
cerchiamo una soluzione del tipo
(x) = c1(x) cos 5x + c2(x) sin 5x
(*)
Da (*) deriva:
'(x) = c1'(x) cos 5x + c2'(x) sin 5x – 5 c1(x) sin 5x + 5 c2(x) cos 5x.
Poniamo c1'(x) cos 5x + c2'(x) sin 5x = 0 (si deve porre cosi!!)
(**)
Da (*) e (**) si ha:
''(x) = – 5 c1'(x) sin 5x + 5 c2'(x) cos 5x – 25 c1(x) cos 5x – 25 c2(x) sin 5x .
Si deve porre allora – 5 c1'(x) sin 5x + 5 c2'(x) cos 5x = e7x
(***)
7x
e a questo punto è la nostra β(x)
(N.B.: per verificare che effettivamente le condizioni “evidenziate” sono quelle da porre,
controlliamo che veramente ''(x) + 25 (x) = e7x : infatti ''(x) + 25 (x) =
= e7x – 25 c1(x) cos 5x – 25 c2(x) sin 5x + 25 c1(x) cos 5x + 25 c2(x) sin 5x = e7x ).
Ricaviamoci ora c1'(x) et c2'(x) risolvendo il seguente sistema:
.
Applicando la regola di Cramer, si ha:
,
,
e quindi
,
.
54 di 65
Calcoliamo ora i due integrali
I2 =
I1 =
,
. Si ha:
I2
I1 =
I2 =
I1
In conclusione possiamo scrivere il seguente sistema:
.
Applicando ancora una volta la regola di Cramer, si ottiene:
(infatti, facendo la prova, D(7e7x cos 5x + 5e7x sin 5x) =
49e7x cos 5x – 35e7x sin 5x + 35e7x sin 5x + 25e7x cos 5x);
(Prova: D(7e7x sin 5x – 5e7x cos 5x) = 49e7x sin 5x + 35e7x cos 5x – 35e7x cos 5x + 25e7x sin 5x).
Quindi,
,
.
Quindi un integrale particolare dell’equazione data è dato da
Effettivamente, si può verificare ciò: infatti, se al posto di
,
ci mettiamo
Si deve avere
,
, come dovevasi dimostrare.
L’integrale generale dell’equazione data è quindi
Ora ricaviamoci c1 e c2 in modo da avere
, si ha:
.
,
.
, quindi
55 di 65
c1 = 1
.
Imponendo
, si deve avere
, cioè c2 = 0.
La funzione y soluzione del nostro problema di Cauchy è quindi
.
Verifichiamo che effettivamente è soluzione. Si deve avere y'' + 25 y = e7x
,
(sin 0 = 0, e0 = 1, )
,
Lo studente è ora invitato a “cimentarsi” con gli esercizi sulle equazioni differenziali lineari a
coefficienti costanti del secondo ordine tratti dai compiti degli anni precedenti.
Modelli Matematici
Molti processi naturali riguardano grandezze che aumentano o diminuiscono con una rapidità
proporzionale al loro valore. Per esempio, la massa di una coltura di batteri che si sviluppano in un
ambiente nutritivo aumenterà con una rapidità proporzionale alla massa stessa. La quantità non
ancora decaduta di una determinata sostanza in un campione radioattivo diminuisce con una rapidità
proporzionale alla quantità stessa, eccetera…
Tutti questi fenomeni possono essere descritti matematicamente nello stesso modo. Se y = y(t)
indica il valore di una grandezza y al tempo t e se y cambia con una rapidità proporzionale al suo
valore, allora si ha:
.
Viene fuori che y è una funzione di tipo esponenziale.
Diremo che la grandezza y esibisce una crescita esponenziale se k > 0 e un decadimento
esponenziale se k < 0.
Esercizio:
Una certa coltura di cellule cresce con una rapidità proporzionale al numero di cellule presenti. Se
la coltura contiene inizialmente 500 cellule e dopo 24 ore 800 cellule, quante cellule vi saranno
dopo altre 12 ore?
Sia y(t) il numero di cellule presenti dopo t ore dall’istante in cui vi erano 500 cellule, istante che
chiameremo “zero”. Allora y(0) = 500 ed y(24) = 800. Poiché
dy = ky dt
log |y| = kt + c
, si ha
(ma y è positivo…)
log y = kt + c
y = ekt+c = ekt ⋅ ec = c1 ekt, dove c1 = ec .
y(0) = c1, quindi y(t) = y(0) ⋅ ekt = 500 ekt.
56 di 65
Quindi 800 = y(24) = 500 e24k da cui
e pertanto
quindi
cioè
.
Vogliamo conoscere y quando t = 36. Si ha:
circa 1012.
Equazione Logistica e Crescita Logistica
Poche grandezze in natura possono continuare a crescere in modo esponenziale per periodi di tempo
estesi, in quanto la crescita è di solito limitata da vincoli esterni. Supponiamo ad esempio che un
numero ridotto di conigli (di ambo i sessi) sia introdotto in una piccola isola che in precedenza era
senza conigli e senza predatori di conigli. Ci si potrebbe attendere che il numero di conigli, in virtù
della loro prolificità, aumenti in modo esponenziale, ma questa crescita sarà limitata alla fine dalla
disponibilità di cibo per i conigli sull’isola. Supponiamo che l’isola possa produrre una quantità di
cibo sufficiente per la sopravvivenza indefinita di una popolazione di L conigli. Se la popolazione al
tempo t conta y(t) conigli, ci aspetteremmo che y(t) cresca con una rapidità proporzionale ad y(t) a
condizione che y(t) sia molto piccolo rispetto ad L. Ma quando y(t) aumenta, diventerà sempre più
difficile per i conigli trovare cibo sufficiente, e allora la loro rapidità di crescita dovrebbe
avvicinarsi a 0 quando y(t) diventa sempre più vicino ad L. Un modello possibile di tale
comportamento è l’equazione differenziale
,
che è chiamata Equazione Logistica, in quanto descrive una crescita che è limitata dalla
disponibilità di risorse necessarie.
Si osservi che
se 0 < y < L e che questa rapidità diventa piccola se y è piccola (vi sono pochi
conigli che si riproducono) oppure se y è prossimo a L (vi sono quasi tanti conigli quanti le risorse
dell’isola lo possono permettere). Se y > L,
: se vi sono più animali di quanto le risorse
possono sostenere, muoiono più conigli di quanti ne nascano. Si può vedere che la soluzione che
soddisfa la condizione iniziale y(0) = y0 (con 0 < y0 <L senza restrizione) è:
(senza restrizione y > 0, L – y >0).
Partiamo dall’equazione
.
L’equazione data è a variabili separabili, perché la si può scrivere anche nel modo:
Passando agli integrali, si ottiene
L
Adesso studiamo il primo integrale con la formula di HERMITE. Poniamo:
,
da cui, per il principio di identità dei polinomi, si deve avere:
A+B=0
– AL = L , da cui A = –1, B = 1.
57 di 65
Quindi
da cui
.
Si ottiene pertanto
da cui, passando agli integrali,
A questo punto ci ricaviamo, nell’ordine: y ; y0 = y(0); C in funzione di y0, e arriveremo al risultato.
Tenendo conto che
ed inoltre
otteniamo
come volevasi dimostrare.
Applicazioni alla fisica
Una delle equazioni fondamentali nella teoria dei circuiti elettrici è
,
dove L (henry) è detta induttanza, R (ohm) resistenza, i (ampère) intensità di corrente ed E (volt)
forza elettromotrice f. e. m.
In questo caso considereremo R ed L costanti positive.
Consideriamo l’equazione differenziale per E(t) = E0 costante:
.
Vogliamo determinare la funzione incognita i = i(t).
(1)
Consideriamo dapprima l’equazione omogenea associata
(con k0 ∈ R costante arbitraria)
58 di 65
Si suppone che l’intensità di corrente sia positiva (perché è una grandezza fisica).
Si ottiene:
che varia in R+ (h costante arbitraria).
, con
Adesso cerchiamo un integrale particolare (cioè una soluzione particolare) dell’equazione data,
attraverso il cosiddetto “metodo della variazione delle costanti arbitrarie”. Cerchiamo dunque una
soluzione dell’equazione differenziale
1.
del tipo:
2.
.
Si ha:
3.
.
Sostituendo le espressioni 2. e 3. nella 1., si ha:
.
Siccome ci basta determinare una soluzione particolare, ci basta scegliere c1 = 0.
Una soluzione particolare è dunque
.
L’integrale generale dell’equazione data sarà quindi la somma dell’integrale generale
dell’omogenea associata e di i0(t), e dunque sarà:
.
Facciamo la prova. Si ha:
Consideriamo il seguente problema di Cauchy:
.
.
La condizione iniziale i(0) = 0 sta ad indicare che all’istante t = 0 non vi è passaggio di corrente
all’interno del circuito. L’integrale generale dell’equazione è:
costante arbitraria.
Imponiamo la condizione iniziale. Si deve avere:
, da cui
, con h
.
59 di 65
Per cui la soluzione del problema è:
.
E = forza elettromotrice
R = resistenza
L = induttanza
C = capacità,
R, L, C quantità positive.
La somma delle cadute di potenziale sugli elementi di un circuito chiuso è uguale alla forza
elettromotrice totale E nel circuito.
La caduta di potenziale ai capi di un resistore di resistenza R (ohm) è Ri, ai capi di un solenoide di
induttanza L (Henry) è
, e ai capi di un condensatore di capacità C (Farad) è
La corrente i (Ampère) e la carica q (coulomb) sono legate dalla relazione
Nel caso preso in esame consideriamo R, L e C costanti.
.
.
L’equazione differenziale del circuito elettrico con induttanza L, resistenza R, capacità C e forza
elettromotrice E(t) è:
equazione che è equivalente, essendo
,
,
, alla seguente:
(3)
da cui si può ricavare q = q(t).
Derivando la (3) e ponendo
abbiamo
, da cui si può ricavare i = i(t).
L’equazione (3) è un’equazione differenziale lineare del secondo ordine a coefficienti costanti.
Dividendo per L si ottiene
.
Esamineremo ora un caso particolare.
Più precisamente: studiare la scarica di un condensatore di capacità C,
attraverso un circuito con induttanza L e resistenza R.
60 di 65
Vogliamo studiare quello che succede quando carichiamo un condensatore e chiudiamo il circuito.
In tal caso supporremo E = 0.
Consideriamo:
L=5
R =10
C=1
q0 = 4
Sostituendo si ha:
.
Consideriamo l’equazione caratteristica associata:
;
.
L’integrale generale è:
, cioè
. Da ciò si ha:
.
Imponiamo le condizioni iniziali per calcolare il valore delle costanti:
q0 = q(0) = c1 + c2
4 = c1 + c2
61 di 65
La soluzione è:
.
62 di 65
Moto Rettilineo
Una massa m viene lanciata verso l’alto dal punto 0 con velocità iniziale v0. Trovare l’altezza
massima raggiunta, ammettendo che la resistenza dell’aria sia proporzionale alla velocità.
Poniamo che il verso verticale positivo sia quello diretto verso l’alto, e che x denoti la distanza della
massa da 0 al tempo t. La massa è sollecitata da due forze, la forza gravitazionale di intensità mg
diretta verso il basso e la resistenza dell’aria di intensità
Tenendo presente il II° principio della dinamica
di verso opposto alla velocità.
kw
si ottiene che l’equazione differenziale è:
, cioè
, da cui
, ove –g è una costante.
)
Consideriamo l’equazione omogenea associata:
. L’equazione caratteristica corrispondente è:
Le radici sono
, e quindi l’integrale generale dell’equazione omogenea associata è:
Per trovare un integrale particolare
dell’equazione
), applichiamo il metodo della variazione
delle costanti arbitrarie. Poniamo
“diventare” funzioni della variabile t), imponiamo che
(cioè: facciamo “variare” c1 e c2, facendole
sia soluzione di ) e calcoliamo '(t).
Si ha:
.
Per il metodo della variazione delle costanti arbitrarie, si
deve porre:
.
Si ottiene dunque
si ha:
Sempre per il metodo della variazione delle costanti arbitrarie, si deve porre:
cioè
ove –g è il nostro (t), secondo la notazione da noi introdotta nelle equazioni
differenziali lineari del secondo ordine a coefficienti costanti.
Si ottiene:
da cui
.
63 di 65
Inoltre
, e dunque
.
Notiamo che stiamo cercando una particolare soluzione (e non una o due famiglie di infinite
soluzioni…), quindi i termini “+ c” e “+ c* ”, nel computo di c2(t) e c1(t), vengono, per così dire,
“trascurati”.
Quindi si ottiene:
,
, pertanto avremo:
.
Quindi l’integrale generale x(t) dell’equazione differenziale ( ) sarà dato da
.
La costante
può essere inglobata in c1, e quindi si può scrivere anche:
.
Il problema che si considera è:
Siano m = 2, k = 1, v0 = 3. Essendo g = 9,8 si ha
.
La soluzione del problema è data da:
.
Imponiamo le condizioni iniziali per determinare il valore delle costanti c1 e c2. Si deve avere:
0 = x(0) = c1 + c2
⇒
c1 + c2 = 0
.
Per cui la soluzione del problema è :
.
64 di 65
Applicazioni delle Equazioni Differenziali lineari del secondo ordine al
moto di un Pendolo:
Un pendolo di lunghezza l e di massa m, sospeso in P (v.
figura) si muove in un piano verticale passante per P.
Trascurando ogni altra forza all’infuori della forza di
gravità (per esempio: attrito, resistenza passiva dell’aria…),
trovare il movimento.
In virtù delle ipotesi, il centro di gravità C del pendolo si
muove sulla circonferenza di centro P e raggio l. Sia ϑ
l’angolo formato dal filo con la verticale al tempo t, e si
supponga che il verso positivo sia quello antiorario. La sola
forza agente è dunque quella di gravità, positiva se il verso
è quello diretto verso il basso, e la sua componente lungo la
tangente alla traiettoria del peso del pendolo è mg sin ϑ.
Se s denota la lunghezza dell’arco C0C, allora s = lϑ (s può
essere interpretato, in un certo senso, come “la misura dell’angolo ϑ ”), e l’accelerazione nei vari
punti dell’arco è:
(l è una costante).
Impostando l’equazione
, si ottiene
ossia .
In virtù del cosiddetto “isocronismo delle piccole oscillazioni”, per ϑ molto piccolo, sin ϑ può
essere “confuso” con ϑ : infatti
formula di Taylor, si ha:
(LIMITE NOTEVOLE) o, se vogliamo, utilizzando la
ϑ + infinitesimi di ordine superiore =
= ϑ + “quantità trascurabili”.
Si ottiene l’equazione
cioè
ossia
Si tratta di un’equazione differenziale lineare del 2° ordine omogenea a coefficienti costanti.
La sua equazione caratteristica associata è:
. L’integrale generale di quest’equazione omogenea è:
.
Si tratta di un esempio di moto armonico.
65 di 65