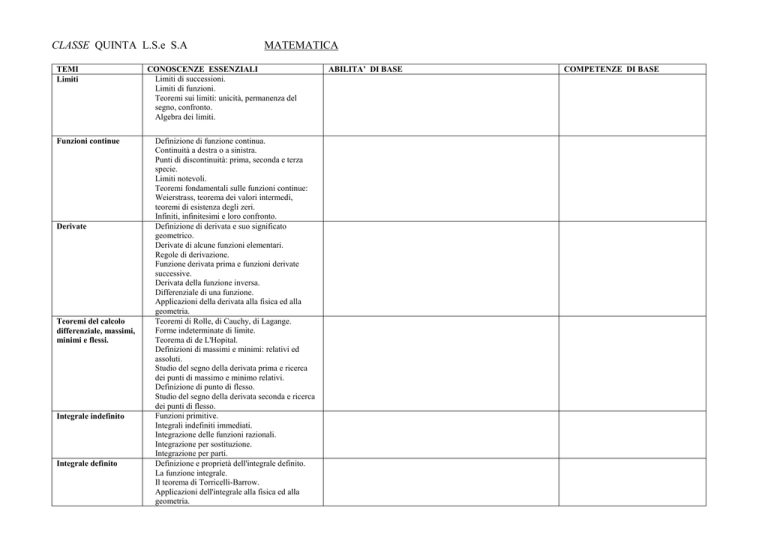
CLASSE QUINTA L.S.e S.A
TEMI
Limiti
Funzioni continue
Derivate
Teoremi del calcolo
differenziale, massimi,
minimi e flessi.
Integrale indefinito
Integrale definito
MATEMATICA
CONOSCENZE ESSENZIALI
Limiti di successioni.
Limiti di funzioni.
Teoremi sui limiti: unicità, permanenza del
segno, confronto.
Algebra dei limiti.
Definizione di funzione continua.
Continuità a destra o a sinistra.
Punti di discontinuità: prima, seconda e terza
specie.
Limiti notevoli.
Teoremi fondamentali sulle funzioni continue:
Weierstrass, teorema dei valori intermedi,
teoremi di esistenza degli zeri.
Infiniti, infinitesimi e loro confronto.
Definizione di derivata e suo significato
geometrico.
Derivate di alcune funzioni elementari.
Regole di derivazione.
Funzione derivata prima e funzioni derivate
successive.
Derivata della funzione inversa.
Differenziale di una funzione.
Applicazioni della derivata alla fisica ed alla
geometria.
Teoremi di Rolle, di Cauchy, di Lagange.
Forme indeterminate di limite.
Teorema di de L'Hopital.
Definizioni di massimi e minimi: relativi ed
assoluti.
Studio del segno della derivata prima e ricerca
dei punti di massimo e minimo relativi.
Definizione di punto di flesso.
Studio del segno della derivata seconda e ricerca
dei punti di flesso.
Funzioni primitive.
Integrali indefiniti immediati.
Integrazione delle funzioni razionali.
Integrazione per sostituzione.
Integrazione per parti.
Definizione e proprietà dell'integrale definito.
La funzione integrale.
Il teorema di Torricelli-Barrow.
Applicazioni dell'integrale alla fisica ed alla
geometria.
ABILITA’ DI BASE
COMPETENZE DI BASE
Equazioni differenziali
Dati e previsioni
Problemi lineari del primo ordine.
L'equazione lineare y'=ay+b.
L'integrale generale dell'equazione differenziale.
Applicazioni per problemi del primo ordine:
legge di caduta dei gravi, circuiti elettrici,
gestione di un presidio, raffreddamento di un
corpo, dinamica delle popolazioni.
L'equazione lineare y'=a(x)y+b(x).
Problemi lineari del secondo ordine.
Oscillazioni del pendolo.
Equazioni lineari del secondo ordine omogenee e
non omogenee.
Applicazioni per problemi del secondo ordine:
carrello sottoposto a forza elastica, circuiti
elettrici, oscillazioni forzate e risonanza.
Distribuzioni di probabilità discrete.
Distribuzione binomiale e di Poisson.
Distribuzioni di probabilità continue.
Distribuzione gaussiana.












