Calcolo dell'integrale circolare
Come è noto, l’integrale indefinito di una funzione integrabile f(x) può essere calcolato come
somma di una qualsiasi primitiva F(x) della f(x) e di una costante arbitraria.
x
In particolare, F(x) può essere la funzione integrale
∫ f (t )dt .
a
Questo metodo può essere applicato per calcolare l’integrale
∫
a 2 − x 2 dx .
x
Consideriamo
∫
a 2 − x 2 dx . Esso rappresenta l’area della parte finita di piano compresa tra l’asse
0
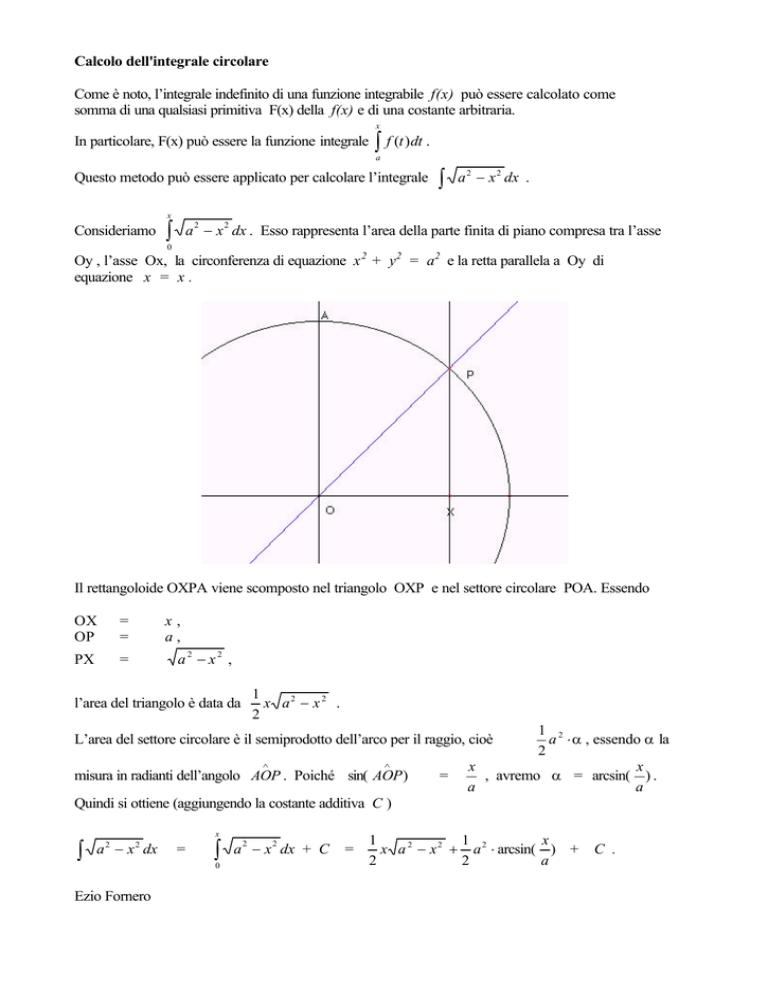
Oy , l’asse Ox, la circonferenza di equazione x 2 + y2 = a2 e la retta parallela a Oy di
equazione x = x .
Il rettangoloide OXPA viene scomposto nel triangolo OXP e nel settore circolare POA. Essendo
OX
OP
=
=
PX
=
x,
a,
a2 − x2 ,
l’area del triangolo è data da
1
x a2 − x 2 .
2
1 2
a ⋅ α , essendo α la
2
x
x
, avremo α = arcsin( ) .
a
a
L’area del settore circolare è il semiprodotto dell’arco per il raggio, cioè
∧
∧
misura in radianti dell’angolo AOP . Poiché sin( AOP )
=
Quindi si ottiene (aggiungendo la costante additiva C )
∫
x
a 2 − x 2 dx
Ezio Fornero
=
∫
0
a 2 − x 2 dx + C
=
1
1
x
x a 2 − x 2 + a 2 ⋅ arcsin( ) +
2
2
a
C .












