Matematica - 14
Funzioni di due variabili
Nello spazio cartesiano (superifici):
z= f ( x , y)
ad ogni coppia ordinata x,y deve corrispondere uno
e un solo valore di z.
-Codominio: è l'insieme dei valori assunti da z
-Dominio: insieme dei valori che x e y possono
assumere, D⊆ℝ (il dominio D è un sottoinsieme
dell'insieme dei numeri reali)
[Se si ha una superficie nello spazio, proiettando tutti i suoi punti sul piano xy, si ottiene il dominio
della funzione]
Per rappresentare una funzione a due variabili:
- uso di software come derive (windows, è a pagamento), geogebra (per linux, windows, mac, è
gratuito);
- curve di livello.
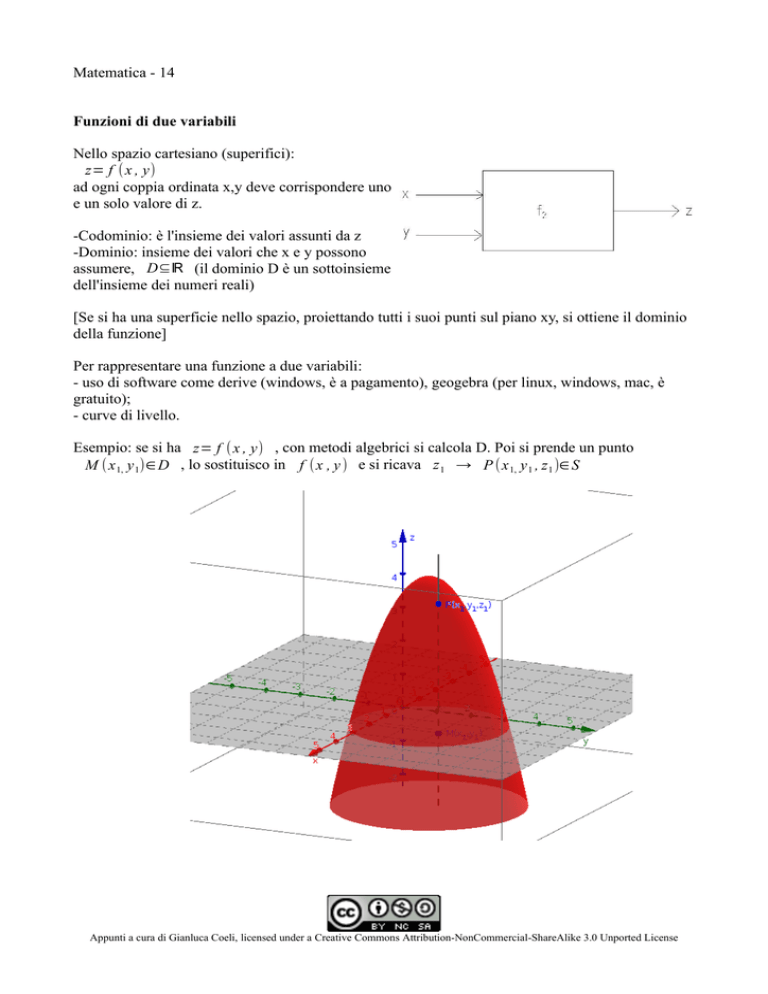
Esempio: se si ha z= f (x , y) , con metodi algebrici si calcola D. Poi si prende un punto
M ( x 1, y 1)∈ D , lo sostituisco in f (x , y ) e si ricava z 1 → P (x 1, y 1 , z 1 )∈ S
Appunti a cura di Gianluca Coeli, licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License
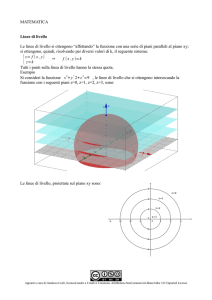
Calcolo del dominio
- Risoluzione grafica di disequazione e sistema di disequazioni in due incognite. Vediamo degli
esempi:
1. Disegniamo le soluzioni delle due
disequazioni:
x>0 e y>0
La soluzione del sistema delle due
disequazioni:
x> 0 (AND)
y >0
è dove sono verificate entrambe, cioè il I
quadrante.
{
2. Disegna la soluzione della disequazione x-y+4>0
Considero l'equazione associata: x-y+4=0, è una retta e la disegno sul piano cartesiano per punti:
x
y
0
4
-4
0
La soluzione è il semipiano superiore o
quello inferiore.
Per trovare la soluzione, prendo il punto
(0,0) e lo sostituisco nella disequazione:
0-0+4>0 e controllo se è vero; in questo
caso sì, quindi i punti del semipiano che
si trovano al disotto della retta verificano
la disequazione.
[Al contrario, se considero il punto (-5,0)
trovo che -5-0+4>0 non è verificata]
Appunti a cura di Gianluca Coeli, licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License
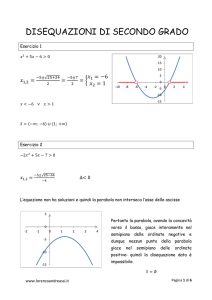
3. Trova la soluzione di −x 2− y 2 +16≥0
L'equazione associata è −x 2− y 2 +16=0 → x 2 + y 2=16 è una circonferenza, quindi la soluzione
può essere costituita da tutti i punti
interni alla circonferenza o da tutti i
punti esterni. Vediamo:
prendo il punto (0,0) e lo sostituisco
nella disequazione
2
2
−0 −0 +16≥0 → 16≥0 Sì,
quindi la soluzione è costituita da tutti i
punti interni alla circonferenza.
La disequazione vista sopra, poteva
essere parte della funzione:
z= √−x 2 − y 2+ 16
per cui la soluzione della disequazione
trovata, è il dominio di questa funzione.
Appunti a cura di Gianluca Coeli, licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License