ALGEBRA Argomento: DISEQUAZIONI IRRAZIONALI Introduzione

Argomento: DISEQUAZIONI IRRAZIONALI
ALGEBRA
Introduzione
Una disequazione si dice irrazionale se la variabile compare sotto il simbolo di radice.
Qualsiasi disuguaglianza tra espressioni contenenti radicali può essere scritta nelle forme generali:
dove p(x) e q(x) sono funzioni di qualsiasi natura.
La soluzione di disequazioni di questo tipo si ottiene applicando il seguente algoritmo:
1. l’indice del radicale, n, è dispari allora la soluzione si ottiene risolvendo una delle seguenti
disequazioni:
2. l’indice del radicale è pari e il simbolo della disequazione è minore (<);
la soluzione si ottiene risolvendo il seguente sistema:
3. l’indice è pari e il simbolo della disequazione è maggiore (>)
la soluzione si ottiene risolvendo i seguenti sistemi:
Appunti di Matematica
1
prof. Teugi Pirozzi
Nota
La condizione p(x) ≥ 0 è necessaria per l’esistenza della radice quando l’indice del radicale è
pari; in tal caso la funzione irrazionale è sempre positiva nel proprio dominio.
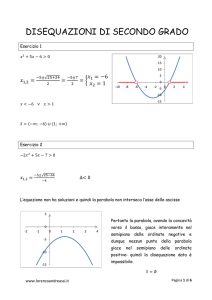
Esempio 1
Risolvere la seguente disequazione irrazionale:
3 x² − 1 ≥ x + 2
L’indice è dispari, quindi la soluzione si ottiene risolvendo la seguente disequazione:
x² − 1 ≥ (x + 2)³
Esempio 2
Risolvere la seguente disequazione irrazionale:
4 − x² < 2 x + 1
L’indice è pari e il simbolo <, quindi la soluzione si ricava risolvendo il sistema:
4 − x ² ≥ 0


2 x + 1 > 0


4 − x² < (2 x + 1)²
Appunti di Matematica
2
prof. Teugi Pirozzi