DISEQUAZIONI DI SECONDO GRADO
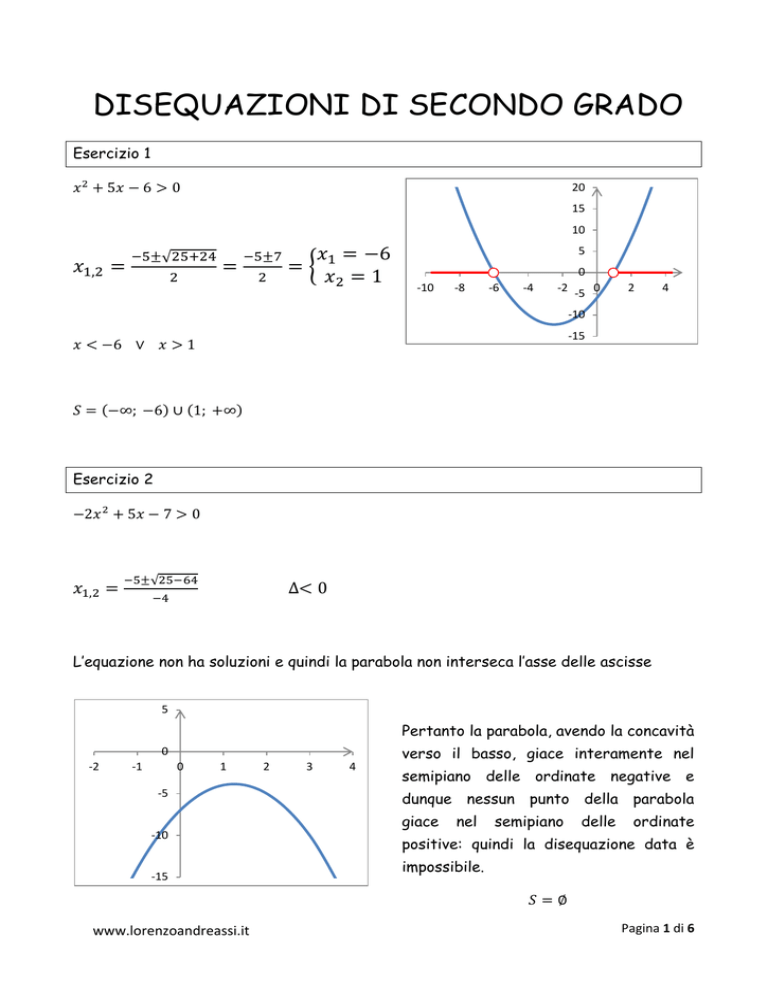
Esercizio 1
20
15
10
5
-10
-8
-6
-4
0
-2 -5 0
2
4
-10
-15
Esercizio 2
L’equazione non ha soluzioni e quindi la parabola non interseca l’asse delle ascisse
5
Pertanto la parabola, avendo la concavità
0
-2
-1
0
1
-5
-10
-15
www.lorenzoandreassi.it
2
3
4
verso il basso, giace interamente nel
semipiano delle ordinate negative e
dunque nessun punto della parabola
giace
nel
semipiano
delle
ordinate
positive: quindi la disequazione data è
impossibile.
Pagina 1 di 6
Esercizio 3
15
10
5
0
-4
-3
-2
-1
0
1
2
3
4
-5
Esercizio 4
Moltiplico ogni fattore per 4 :
Risulta
15
; l’equazione ha perciò due
soluzioni coincidenti. La parabola, che
volge la concavità verso l’alto, è tangente
10
all’asse
nel punto
. Quindi
tutti i punti si trovano nel semipiano delle
ordinate positive, eccetto il punto
5
che
si trova sull’asse . Perciò la disequazione
data è soddisfatta per qualunque valore
0
-1
0
1
2
3
4
5
6
7
8
di .
L’insieme delle soluzioni è :
.
-5
www.lorenzoandreassi.it
Pagina 2 di 6
Esercizio 5
Moltiplico ogni fattore per 9:
La parabola volge la concavità verso il
10
basso ed è tangente all’asse
0
-3-10 0
3
6
9
12
15
nel punto
. Tutti i punti della parabola,
18
-20
eccetto
-30
ordinate negative. Perciò la disequazione
-40
data è soddisfatta da qualunque valore,
-50
eccetto
-60
, giacciono nel semipiano delle
. Quindi possiamo esprimere
le sue soluzioni scrivendo:
-70
-80
-90
L’insieme delle soluzioni è pertanto:
-100
Esercizio 6
Questa parabola volge la concavità verso il
10
basso ed è tangente all’asse
0
-5
-4
-3
-2
-1
0
-10
1
nel punto
. Tutti i punti della parabola
2
hanno ordinata negativa, eccetto il punto
-20
la cui ordinata è zero. Perciò l’unico valore
-30
di
che soddisfa la disequazione data è:
e
-40
-50
www.lorenzoandreassi.it
l’insieme
delle
soluzioni
è:
.
Pagina 3 di 6
Esercizio 7
Le
due
disequazioni,
già
in
forma
canonica,
devono
essere
verificate
contemporaneamente, cioè per gli stessi valori di .
Prima disequazione:
10
Quindi:
8
6
E l’insieme delle soluzioni risulterà:
4
2
0
-3 -2,5 -2 -1,5 -1 -0,5 0
-2
0,5
1
1,5
2
-4
Seconda disequazione:
Quindi:
9
7
5
E l’insieme delle soluzioni risulterà:
3
1
-1 0 0,5 1 1,5 2
-3 -2,5 -2 -1,5 -1 -0,5
-3
-5
I valori di
che verificano entrambe le disequazioni sarà:
S2
S1
-2
-1
www.lorenzoandreassi.it
1/4
1/3
Pagina 4 di 6
Esercizio 8
19
Prima disequazione:
Seconda disequazione:
Terza disequazione: ………
14
9
4
-1
-5 -4 -3 -2 -1 0 1 2
Poiché una delle disequazioni del sistema è impossibile, ossia non ha soluzioni, non
possono esistere numeri che soddisfino contemporaneamente tutte le disequazioni
del sistema: pertanto non è necessario procedere alla risoluzione della terza
disequazione. IL SISTEMA è IMPOSSIBILE ed è quindi :
.
Esercizio 9
Occorre ora studiare il segno del numeratore
19
e quello del denominatore e applicare la regola
dei segni con l’aiuto del solito schema.
14
NUMERATORE:
9
4
-2
-1
-1 0
1
2
3
4
5
-6
www.lorenzoandreassi.it
Pagina 5 di 6
6
DENOMINATORE 1:
DENOMINATORE 2:
STUDIO DEL SEGNO:
+
-
0,3
+
0,7
-
2
+
3,3
Quindi la soluzione risulta essere:
Ovvero, con gli intervalli:
www.lorenzoandreassi.it
Pagina 6 di 6