Matematica - 10
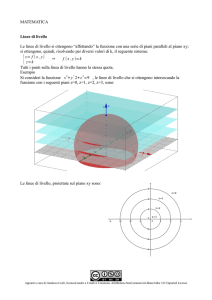
Calcolo del volume del cono e della sfera con l'integrale definito
Dalla geometria sappiamo che:
1 2
il volume del cono è: V = π r h
3
4 3
il volume della sfera è: V = π r
3
Verifichiamo queste due formule utilizzando l'integrale definito
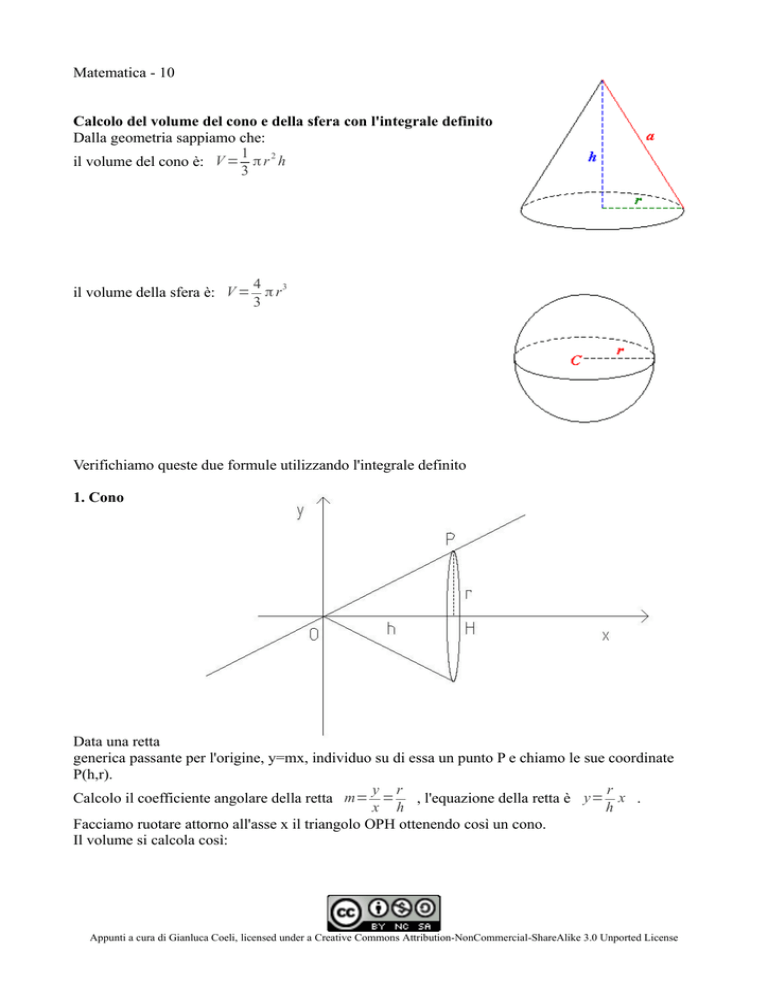
1. Cono
Data una retta
generica passante per l'origine, y=mx, individuo su di essa un punto P e chiamo le sue coordinate
P(h,r).
y r
r
Calcolo il coefficiente angolare della retta m= = , l'equazione della retta è y= x .
x h
h
Facciamo ruotare attorno all'asse x il triangolo OPH ottenendo così un cono.
Il volume si calcola così:
Appunti a cura di Gianluca Coeli, licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License
h
V =π∫0
[ ]
h
r 2
r2 h 2
r 2 x3
r2 h3 1 2
x dx=π 2 ∫0 x dx=π 2
=π 2
= π r h c.v.d.
h
3
h
h 3 0
h 3
( )
( )
2. Sfera
L'equazione della circonferenza è
x 2 + y 2=r 2
esplicitando la y:
y=±√ r 2−x 2
ma questa non è l'equazione di una
funzione; perché lo diventi, si deve
scegliere o la parte positiva o la parte
negativa.
Scegliamo la radice positiva:
y=√ r 2−x 2
il diagramma cartesiano di questa
funzione è una semicirconferenza.
Se si fa ruotare questa
semicirconferenza si ottiene una sfera.
Calcoliamo il volume della sfera:
r
V =π∫−r ( √ r −x
=2 π
2
2
)
2
r
2
2
r
[
2
dx=2 π ∫0 (r −x ) dx=2 π r x−
] (
x3
r3
3r 3 −r 3
2
=2 π r r− =2 π
=
3 0
3
3
) (
)
2r 3 4 3
= π r c.v.d.
3
3
( )
Esercizio
Calcolare l'area compresa tra le due funzioni e il volume del solido di rotazione:
1
1
g ( x)= x 2 , f (x )=− x 2 + 2x
2
2
Trovo le intersezioni tra le due funzioni:
1
1
1
y= x 2
y= x 2
1
y= x 2
y= x 2
2
2
y=0 y=2
2
2
1
1 2
1
x=0 x=2
y=− x 2 +2x
x =− x 2 + 2x x 2−2x=0 x (x−2)=0
2
2
2
Si disegnano poi le due curve, calcolando anche i valori
delle ordinate per x=1:
1
3
y=
y=
2
2
x=1 x=1
L'area compresa tra le due curve si calcola così:
{
{
{
{
{
{
{ {
Appunti a cura di Gianluca Coeli, licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License
2
S =∫0
[
[
]
2
2
1 2
1 2
x3 2
8
−8+12 4
2
− x +2x− x dx=∫0 (−x + 2x)dx= − + x =− + 4=
=
2
2
3
3
3
3
0
]
Il volume si calcola:
2
2
1
1
V =π∫0 − x 2 + 2x − x 2
2
2
[(
) ( )]
( 14 x +4x −2x − 14 x ) dx=
x
x
4
1
32
32−24 8
=π [ 4 −2 ] =π ( 8− 16)=π ( −8 )=π
= π
3
4
3
2
3
3
3
3
2
2
dx=π ∫0
4
2
3
4
4 2
0
Appunti a cura di Gianluca Coeli, licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License