Esempio 19
Studiare dominio e segno della
seguente funzione:
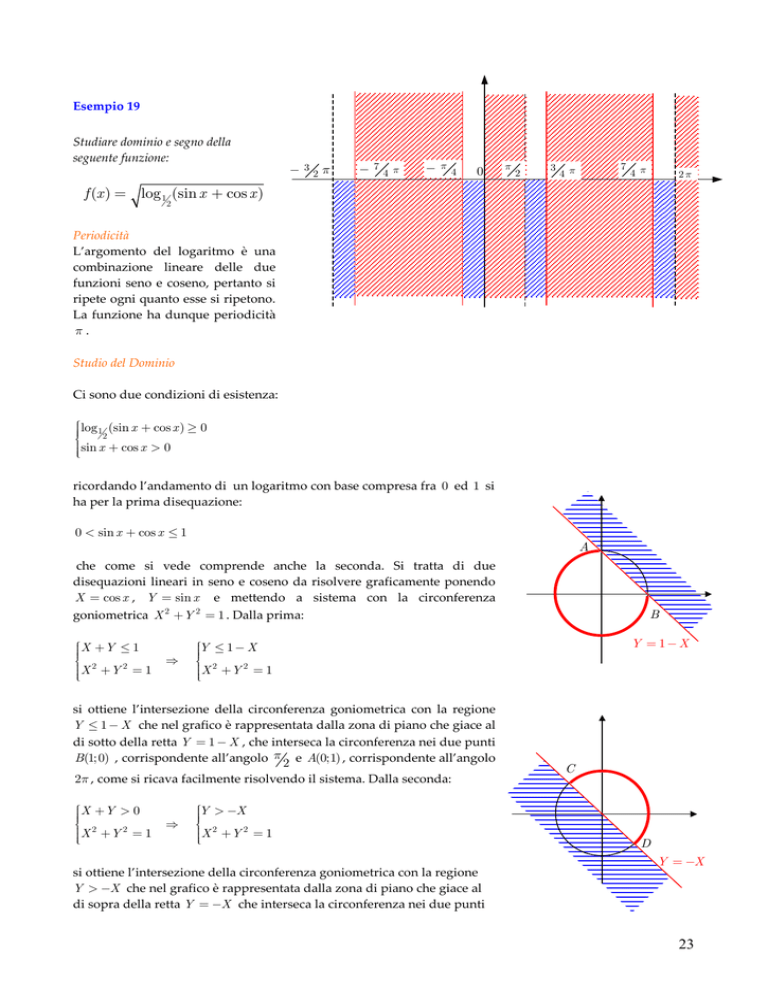
− 32π
−74π
−π4
0
π
2
3
7
4 π
4 π
2π
f (x ) = log 1 (sin x + cos x )
2
Periodicità
L’argomento del logaritmo è una
combinazione lineare delle due
funzioni seno e coseno, pertanto si
ripete ogni quanto esse si ripetono.
La funzione ha dunque periodicità
π.
Studio del Dominio
Ci sono due condizioni di esistenza:
log 1 (sin x + cos x ) ≥ 0
2
+ cos x > 0
sin
x
ricordando l’andamento di un logaritmo con base compresa fra 0 ed 1 si
ha per la prima disequazione:
0 < sin x + cos x ≤ 1
A
che come si vede comprende anche la seconda. Si tratta di due
disequazioni lineari in seno e coseno da risolvere graficamente ponendo
X = cos x , Y = sin x e mettendo a sistema con la circonferenza
goniometrica X 2 + Y 2 = 1 . Dalla prima:
X +Y ≤ 1
2
X +Y 2 = 1
⇒
2π , come si ricava facilmente risolvendo il sistema. Dalla seconda:
⇒
Y = 1−X
Y ≤ 1− X
2
X +Y 2 = 1
si ottiene l’intersezione della circonferenza goniometrica con la regione
Y ≤ 1 − X che nel grafico è rappresentata dalla zona di piano che giace al
di sotto della retta Y = 1 − X , che interseca la circonferenza nei due punti
B(1; 0) , corrispondente all’angolo π 2 e A(0;1) , corrispondente all’angolo
X + Y > 0
2
X +Y 2 = 1
B
Y > −X
2
X +Y 2 = 1
si ottiene l’intersezione della circonferenza goniometrica con la regione
Y > −X che nel grafico è rappresentata dalla zona di piano che giace al
di sopra della retta Y = −X che interseca la circonferenza nei due punti
C
D
Y = −X
23
π
(
)
C − 2 2 ; 2 2 , corrispondente all’angolo 3 4 π , e
(
2
)
2
2 ;− 2 ,
2
3 π
4
corrispondente all’angolo 7 4 π , come si trova facilmente risolvendo
il sistema. Intersecando la due condizioni sulla circonferenza
goniometrica si ottiene infine il dominio della funzione:
π
7
3
D : + 2k π; π + 2k π ∪ π + 2k π;2π + 2k π
4
4
2
2π
k ∈ℤ
7 π
4
Studio del Segno
Una radice di indice pari, laddove esiste è senz’altro positiva, quindi si ha f (x ) ≥ 0 ∀x ∈ D
Esempio 20
Studiare dominio e segno della seguente funzione:
f (x ) =
x +2
x − x +2
−2
0
2
Studio del Dominio
Ci sono due condizioni di esistenza:
x + 2 ≥ 0
x − x +2 ≠ 0
Risolviamo la seconda condizione, posta in forma di equazione x = x + 2 , elevando al quadrato ambo i
membri. Questa operazione introduce soluzioni aggiuntive, quindi dovremo verificare i risultati ottenuti
inserendoli nell’espressione originaria:
1± 1+8
⇒ x1 = 2, x 2 = −1
2
Come si vede la soluzione x = −1 non soddisfa l’equazione originaria avendosi −1 − −1 + 2 = −2 ≠ 0 , e
va pertanto scartata. Si ottiene allora:
x2 = x + 2
⇒
x2 − x − 2 = 0
⇒
x=
D : [−2;2) ∪ (2; +∞)
Studio del Segno
Segno del numeratore:
x +2 ≥ 0
⇒
x ≥ −2
segno del denominatore:
x − x +2 > 0
⇒
x > x +2
24
risolviamo graficamente confrontando i grafici delle due
curve:
2
y =x
x0
−2
y = x +2
y 2 = x + 2
y ≥ 0
⇒
⇒
x = y 2 − 2
y ≥ 0
La prima è la bisettrice del primo e terzo quadrante, la seconda il ramo di parabola orizzontale con vertice
V (−2; 0) e concavità nel verso crescente della ascisse. La soluzione è la regione in cui la retta sovrasta il
grafico della parabola, quindi a destra del punto x 0 in figura. Troviamo le intersezioni fra parabola e retta
elevando al quadrato l’equazione x = x + 2 :
x2 = x + 2
⇒
x2 − x − 2 = 0
⇒
x=
1± 1+8
2
⇒
x1 = 2, x 2 = −1
Anche qui la soluzione x = −1 è da scartare, perché costituisce
l’intersezione con il ramo negativo di parabola, come si vede in figura.
Pertanto il denominatore risulta positivo se x > 2 . Eseguiamo il prodotto
dei segni:
segno di:
−2
−1
2
2
x +2
+
+
x − x +2
−
−
+
+
25












