L`integrale for dummies

L’integrale for dummies
Consideriamo una funzione F (x ) , volutamente indicata con la lettera F maiuscola, e la sua derivata F (x ) .
F
, quindi quanto più x si avvicina a zero, tanto migliore è
x 0 x
Sappiamo che F (x )  lim
l’approssimazione:
F (x ) 
F
x
F (x )x  F

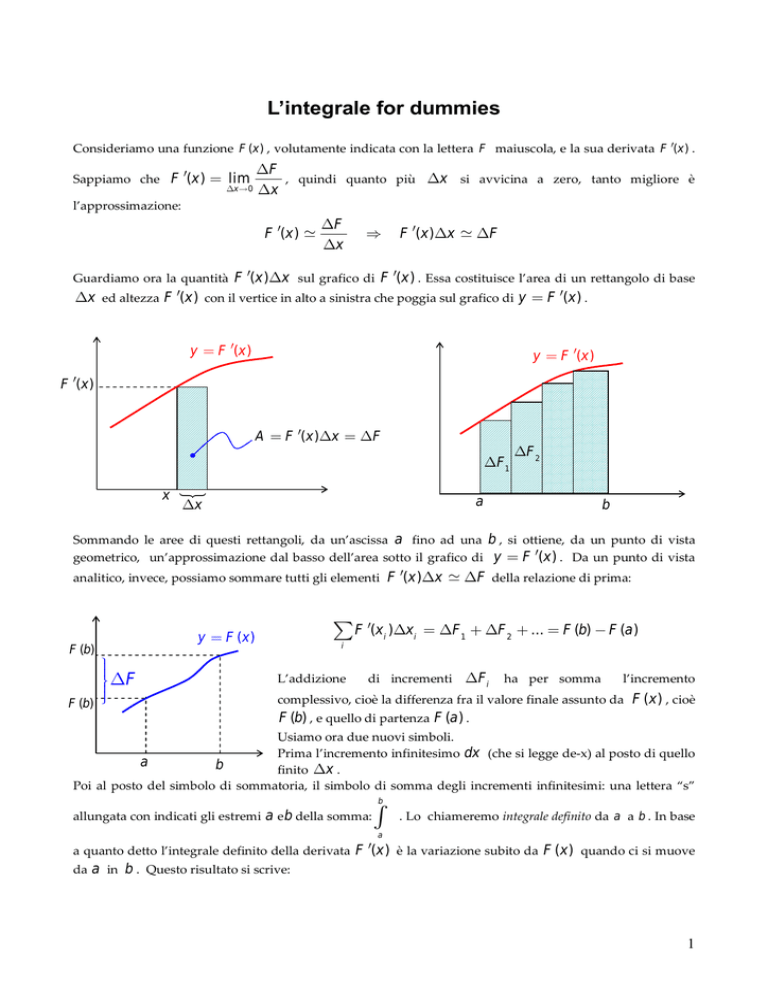
Guardiamo ora la quantità F (x )x sul grafico di F (x ) . Essa costituisce l’area di un rettangolo di base
x ed altezza F (x ) con il vertice in alto a sinistra che poggia sul grafico di y  F (x ) .
y  F (x )
y  F (x )
F (x )
A  F (x )x  F
F1
x 
x
F2
a
b
Sommando le aree di questi rettangoli, da un’ascissa a fino ad una b , si ottiene, da un punto di vista
geometrico, un’approssimazione dal basso dell’area sotto il grafico di y  F (x ) . Da un punto di vista
analitico, invece, possiamo sommare tutti gli elementi F (x )x  F della relazione di prima:
F (b )

 F


F (b ) 
y  F (x )
 F (x )x
i
i
L’addizione
i
 F1  F2  ...  F (b)  F (a )
di incrementi Fi
ha per somma
l’incremento
complessivo, cioè la differenza fra il valore finale assunto da F (x ) , cioè
F (b) , e quello di partenza F (a ) .
Usiamo ora due nuovi simboli.
Prima l’incremento infinitesimo dx (che si legge de-x) al posto di quello
a
b
finito x .
Poi al posto del simbolo di sommatoria, il simbolo di somma degli incrementi infinitesimi: una lettera “s”
b
allungata con indicati gli estremi a e b della somma:

. Lo chiameremo integrale definito da a a b . In base
a
a quanto detto l’integrale definito della derivata F (x ) è la variazione subito da F (x ) quando ci si muove
da a in b . Questo risultato si scrive:
1
y  F (x )
b
 F (x )dx  F (b)  F (a )
a
F
Il senso di tutto questo è che se vogliamo calcolare l’area compresa fra il
grafico di una funzione y  f (x ) , l’asse delle ascisse e le due rette verticali
x  a ed x  b dobbiamo immaginare che la funzione in questione sia la
derivata di un’altra funzione F (x ) , che viene detta primitiva, quindi calcolare
a
b
la differenza F (b)  F (a ) ed avremo l’area.
b
y  f (x )
F (x )  f (x )


Area 
 f (x )dx  F (b)  F (a)
a
Risalire ad F (x ) nota y  f (x ) non è semplice, (in certi casi addirittura impossibile), ed occorrerà escogitare
una procedura che permetta di tornare indietro rispetto all’operazione di derivazione.
Esempio
Calcolare l’area sottesa dall’arco di curva y  x 3 delimitata dalle rette
x  1 ed x  2
Dobbiamo
calcolare
la
primitiva
della
funzione
y  x3
y  x3 .
Consideriamo il caso più generale y  x n : come sappiamo la
derivata di un monomio si ottiene con la formula y   nx n 1 . Una
semplice verifica permette di dimostrare che una possibile primitiva
è allora:
F (x ) 
1
x n 1
n 1

F (x ) 
1
n 1
(n  1)  x n 11  x n  f (x )
1
2
La totalità delle primitive si ottiene considerando il caso più generale in cui nella funzione originale possa
esserci un termine costante C che scompare nella derivazione:
f (x )  x n

F (x ) 
1
x n 1
n 1

F (x )  f (x )
Nel caso proposto si ha:
f (x )  x 3

F (x ) 
1
1
x 31  C  x 4  C
3 1
4
E quindi l’area richiesta vale:
2

1
2
 13
1

23

x 3dx  F (2)  F (1)   x 3  C  
 C    C
4

 4
4

1
 7
 

 4
2
Il simbolo   significa che la funzione fra parentesi quadre deve essere calcolata nell’estremo superiore ed a
1
tale valore va sottratto quello calcolato nell’estremo inferiore. Notare che la costante di integrazione C non
influisce mai sul calcolo dell’aria in quanto compare sempre due volte ma con segno opposto.
2