TESTO ADOTTATO
# $# $
+
%# ,
" %&
'
!
"
# $
()* $
$
&
$
1) LE FUNZIONI. Definizione e terminologia, equazione, grafico, classificazione e determinazione
del dominio di funzioni reali di variabile reale; funzioni composte; funzioni pari e funzioni dispari;
funzioni crescenti e decrescenti in un intervallo.; funzioni monotóne.
2) LIMITI DI FUNZIONI. Definizione di limite finito o infinito di una funzione per x → c o per
x → ±∞ , limite destro e sinistro di una funzione in un punto; rappresentazione dei limiti nel piano
cartesiano; operazioni sui limiti: limite della somma, della differenza, del prodotto e del quoziente
di due funzioni (senza dimostrazione). Limite per x → ±∞ del quoziente di due polinomi.
3) IL CALCOLO DEI LIMITI E LE FUNZIONI CONTINUE. Il calcolo dei limiti e le forme
indeterminate per limiti di funzioni algebriche razionali intere e fratte; definizione di funzione
continua in un punto e in un intervallo; i casi di discontinuità di una funzione.
4) LA DERIVATA DI UNA FUNZIONE E I TEOREMI DEL CALCOLO DIFFERENZIALE.
Rapporto incrementale; derivata di una funzione in un punto; derivata di una funzione in un
intervallo; significato geometrico della derivata; equazione della tangente al grafico di una funzione
derivabile; teorema di continuità delle funzioni derivabili (con dimostrazione); derivate di funzioni
elementari; casi di funzioni non derivabili: derivata infinita, cuspidi, punti angolosi; regole di
derivazione (derivata della somma, della differenza, del prodotto, del quoziente di funzioni – senza
dimostrazione); derivata di funzione di funzione; derivate di ordine superiore; regola di de
l’Hôpital.
5) LO STUDIO DELLE FUNZIONI. Funzioni crescenti e decrescenti in un punto e in un intervallo;
punti stazionari: massimi, minimi e flessi a tangente orizzontale; la derivata seconda: concavità e
convessità del grafico di una funzione; punti di flesso a tangente obliqua; asintoti orizzontali,
verticali e obliqui; costruzione del grafico di una funzione razionale intera o fratta.
6) INTERPRETAZIONE RAGIONATA DEL GRAFICO DI UNA FUNZIONE
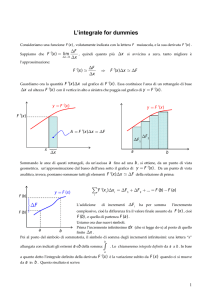
7) ELEMENTI DI CALCOLO INTEGRALE. Funzioni primitive, integrale indefinito; integrali
indefiniti immediati; proprietà dell’integrale indefinito; integrali indefiniti immediati di funzioni
razionali intere; integrale definito; formula fondamentale del calcolo integrale.
!" " #$$%
&&
'"
( "