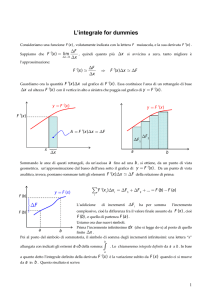
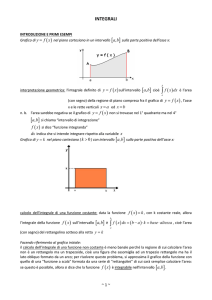
ISTITUZIONI DI MATEMATICHE
(Scienze Naturali)
Tema di preparazione al secondo compitino 2014/2015
Cognome....................................Nome.........................Matricola..............
A
Calcolare una primitiva di ciascuna delle seguenti funzioni
f (x) = 2x3 +cos(1−x),
g(x) =
3
,
2(3x + 2)3
h(x) =
√
3
x2 +
x2
2
+1
B
Calcolare il seguente integrale definito
Z
0
√
4 3 2x + 8dx.
−4
C
C1) Determinare il polinomio di Taylor di ordine 3, centrato in x0 =
0, della funzione f (x) = sin(3x).
C2) Utilizzare il risultato del punto C1 per calcolare
3x − sin(3x)
x→0
x3
lim
D
D1) Dare la definizione di primitiva di una funzione continua f :
R → R?
1
2
D2) Quale tra le seguenti funzioni è una primitiva di f ?
Z
F (x) =
1
Z
f (t)dt, G(x) =
0
x
f (t)dt, H(x) = f 0 (x) + k.
1
E
Scrivere l’equazione della retta tangente in x0 = 1 al grafico della
funzione
g(x) = xe3x−1 .
F
F1) Determinare l’area A della regione di piano compresa tra l’asse
x, il grafico della funzione y = 3sin(2x), le rette x = 0 e x = π2 .
F2) Calcolare
Z
π
2
2cos(2x)dx.
I=
− π2
G
G1) Dare la definizioni di asintoto obliquo per una funzione reale di
variabile reale.
G2) Data la funzione
f (x) =
3x3 − 2
x2 − 1
determinare gli asintoti (orizzontali, verticali e obliqui) di f.
3
H
Se F1 e F2 sono primitive della stessa funzione f nell’intervallo [a, b]
che cosa si può dire della differenza F1 − F2 ?
È vero che F = sin(x) + 5 è una primitiva di f = cos(x)?
È vero che F = sin(x) è una primitiva di f = cos(x) + 3?
I Studiare (senza ricorrere alla derivata seconda) il grafico della funx2 −9
zione f (x) = e x−1 + 3.
L Disegnare il grafico (approssimativo) di una funzione f (x) tale che
soddisfi contemporaneamente a tutte le seguenti richieste
• sia definita e continua in (−∞, 0) ∪ (0, ∞)
• non sia iniettiva
• lim f (x) = −3
x→−∞
• lim f (x) = 2
x→∞
M Disegnare il grafico (approssimativo) di una funzione f (x) tale
che soddisfi contemporaneamente a tutte le seguenti richieste
•
•
•
•
•
•
N
sia definita in (−∞, ∞)
non sia continua in x0 = 2
come funzione f : R → R sia suriettiva
non abbia asintoti verticali
passi per (−4. − 4)
abbia la retta y = x come asintoto obliquo.
4
N1) Dare la definizone di integrale defintito di una funzione in un
intervallo [a, b].
N2) Calcolare l’area della regione limitata di piano compresa tra le
curve di equazioni rispettive:
y = x2 e y = −x + 3.
O
Studiare la seguente funzione (non è richiesto lo studio della derivata
seconda) e se ne fornisca un grafico qualitativo.
f (x) = 3x
2 +x+2
− 9.
P
P1) Enunciare il teorema di Rolle.
P2) Stabilire a quali tra le seguenti funzioni può essere applicato il
teorema di Rolle nell’intervallo [−π, π] e perché.
f1 (x) = sin(x),
f2 (x) =
1
,
x2
f3 (x) = (x+π)(x−π),
f4 (x) = |x|.
5
Q Disegnare il grafico (approssimativo) di una funzione f (x) tale che
soddisfi contemporaneamente a tutte le seguenti richieste
•
•
•
•
sia definita e derivabile in (−∞, ∞)
sia tale che f 0 (x) = 0 se e solo se x = −1, 2, 4
sia crescente in (−∞, 2) ∪ (4, ∞)
abbia per immagine f (R) = (−∞, 5)
R
P1) Enunciare il teorema fondamentale del calcolo integrale e la formula fondamentale del calcolo integrale.
P2) Dare un esempio di funzione f (x) (non identicamente nulla) tale
che sia
2
Z
f (x)dx = 0.
−2
S
S1) Dare la definizione di media di una funzione in un intervallo..
S2) Calcolare la media nell’intervallo [0, 1] di ciascuna delle seguenti
funzioni:
f (x) = x,
g(x) = x3 ,
h(x) =
√
3
x.