INTEGRALI
INTRODUZIONE E PRIMI ESEMPI
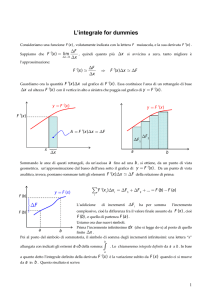
Grafico di y f x nel piano cartesiano in un intervallo a, b sulla parte positiva dell’asse x:
interpretazione geometrica: l’integrale definito di y f x sull’intervallo a, b cioè
b
f x dx
è l’area
a
(con segno) della regione di piano compresa fra il grafico di y f x , l’asse
x e le rette verticali x a ed x b
n. b. l’area sarebbe negativa se il grafico di y f x non si trovasse nel 1° quadrante ma nel 4°
a, b si chiama “intervallo di integrazione”
f x si dice “funzione integranda”
dx indica che si intende integrare rispetto alla variabile x
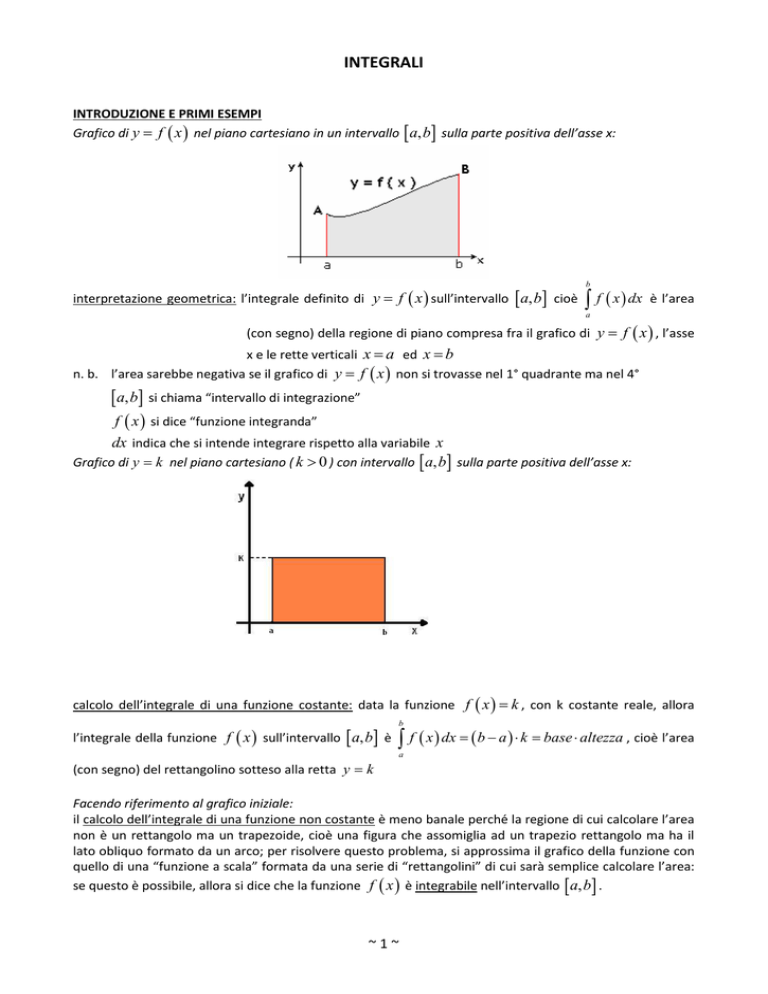
Grafico di y k nel piano cartesiano ( k 0 ) con intervallo a, b sulla parte positiva dell’asse x:
calcolo dell’integrale di una funzione costante: data la funzione f x k , con k costante reale, allora
l’integrale della funzione f x sull’intervallo a, b è
b
f x dx b a k base altezza , cioè l’area
a
(con segno) del rettangolino sotteso alla retta y k
Facendo riferimento al grafico iniziale:
il calcolo dell’integrale di una funzione non costante è meno banale perché la regione di cui calcolare l’area
non è un rettangolo ma un trapezoide, cioè una figura che assomiglia ad un trapezio rettangolo ma ha il
lato obliquo formato da un arco; per risolvere questo problema, si approssima il grafico della funzione con
quello di una “funzione a scala” formata da una serie di “rettangolini” di cui sarà semplice calcolare l’area:
se questo è possibile, allora si dice che la funzione f x è integrabile nell’intervallo a, b .
~1~
b
procedimento per calcolare
f x dx :
a
trovare una funzione F x che, nell’intervallo a, b , abbia f x come derivata cioè una “primitiva”
di f x
calcolare il valore di F x negli estremi dell’intervallo di integrazione, cioè calcolare F b e F a
b
sottrarre questi 2 valori, quindi
f x dx F x
b
a
F b F a
a
5
5
esempio: 3x 2 dx x3 53 23 125 8 117
2
2
in questo caso una “primitiva” di 3x 2 , cioè una funzione che derivata diventa 3x 2 , è x 3
n. b. il passaggio più impegnativo del procedimento per calcolare un integrale è il 1°, cioè trovare una
funzione “primitiva”, perché gli altri 2 sono molto semplici
PRIMITIVE ELEMENTARI E PROPRIETÀ DEGLI INTEGRALI
definizione: si dice che F x è una “primitiva” di f x se F ' x f x in tutto l’intervallo a, b
osservazioni:
non tutte le funzioni f x hanno una primitiva, ma ce l’hanno sempre per le funzioni continue
la primitiva non è unica, infatti se F x è una primitiva allora lo sono anche F x c ( c = n° reale
costante) – sono primitive di 3x 2 non solo x 3 ma anche x 3 1 , x3 2 , x3 3 , ... e per indicare una
generica primitiva di f x si usa la notazione
f x dx detta anche integrale indefinito di f x
le primitive di alcune funzioni si possono determinare facilmente utilizzando la nota tabella delle derivate:
primitive elementari
funzione f x
primitiva F x
x n (n 1)
x n 1
n 1
2 x
1
x
1
x2
ex
1
x
1
x
ex
ln x
2
x 4 16 1 15
esempio: x dx
4
4
4 4
1
1
2
3
x4
x4
1 invece di
il risultato sarebbe stato identico prendendo come primitiva
perché la
4
4
costante 1, nei calcoli successivi, sarebbe prima stata aggiunta e poi sottratta.
proprietà elementari degli integrali
a)
b)
f x g x dx f x dx g x dx
K f x dx K f x dx
esempio: 3x e x dx 3xdx e x dx 3
x2
e x (sono state applicate prima la proprietà a, poi la b)
2
~2~
b
c)
a
c
b
a
c
f x dx f x dx f x dx con a c b (facile comprenderla con l’interpretazione grafica)
PRIMITIVE DI DERIVATE DI FUNZIONI COMPOSTE
ricordando la regola di derivazione delle funzioni composte
f g x ' f ' g x g ' x
è possibile
calcolare alcuni integrali apparentemente complessi:
esempio:
2e
2x
dx e 2 x (perché la derivata della funzione composta e 2 x è 2e 2 x )
2x
1
dx ln x 2 1 (perché la derivata della funzione composta ln x 2 1 è 2
2x )
1
x 1
1
2
1
1
esempio:
(perché la derivata della funzione composta
è
dx
2 )
2
2
2x 3
2x 3
2 x 3
2 x 3
esempio:
x
2
purtroppo non tutti gli integrali sono facilmente risolvibili con questo procedimento, perciò esistono altre
tecniche come quella per parti o per sostituzione; con quest’ultimo metodo possono essere risolti anche gli
ultimi esempi riportati.
INTEGRAZIONE PER PARTI
regola di integrazione per parti:
f x g ' x dx f x g x f ' x g x dx
n. b. conviene scegliere come funzione f quella più semplice da derivare e come funzione g ' quella più
facile da integrare
esempio:
xe dx xe 1 e dx xe
x
x
x
x
ex
in questo caso f x e g ' e x quindi f ' 1 e g e x (è stato scelto f x e non f e x
perché x ha una derivata più semplice di e x , cioè 1; inoltre e x è facile da integrare)
esempio:
x2
x2 1
x2
1
x2
1
ln x dx ln x xdx ln x x 2
2
2 x
2
2
2
4
2
x
1
in questo caso f ln x e g ' x quindi f ' e g
(è stato scelto g ' x e non
x
2
g ' ln x perché ln x non è facile da integrare)
x ln xdx
INTEGRAZIONE PER SOSTITUZIONE
regola di integrazione per sostituzione (integrale indefinito): si usa in caso di funzioni composte f g x
indicare con y la funzione “più interna” della funzione composta, cioè g x
effettuare le opportune sostituzioni senza dimenticare dx
esempio:
e
2 x 1
dx si pone 2 x 1 y da cui 2dx dy dx
1
dy
2
si sostituisce ottenendo:
1
1
1
1
dx e y dy e y dy e y e 2 x 1
2
2
2
2
1
1
dx
esempio:
si pone 5 x 3 y da cui 5dx dy dx dy
2
5
5 x 3
e
2 x 1
1
5 x 3
2
dx
si sostituisce:
1 1
1 1
1
dy
2
y 5
5 y
5 5 x 3
n. b. in caso di integrali definiti, è necessario sostituire anche gli estremi dell’intervallo di integrazione a e b
come già mostrato nell’esempio di pagina 2
~3~