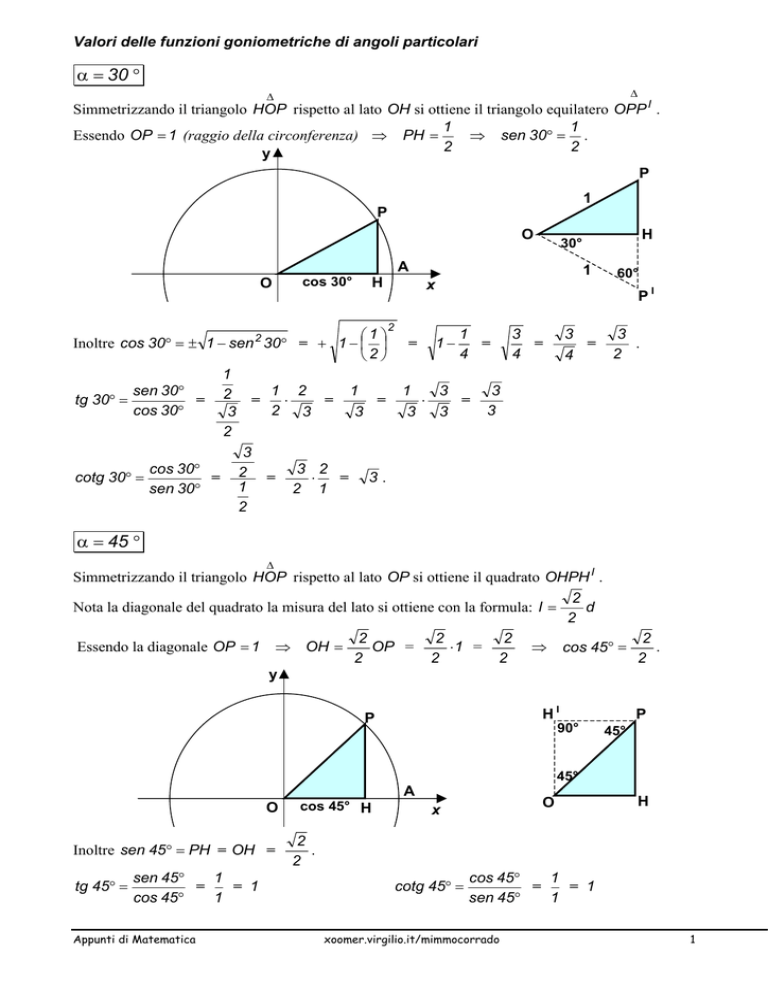
Valori delle funzioni goniometriche di angoli particolari
α = 30 °
∆
∆
Simmetrizzando il triangolo HOP rispetto al lato OH si ottiene il triangolo equilatero OPP I .
1
1
Essendo OP = 1 (raggio della circonferenza) ⇒ PH =
⇒ sen 30° = .
2
2
y
P
1
60°
P
30°
30°
O
O
A
30°
cos 30°
H
H
1
x
60°
PI
2
1
3
⎛1 ⎞
Inoltre cos 30° = ± 1 − sen 2 30° = + 1 − ⎜ ⎟ = 1 −
=
=
4
4
⎝2⎠
1
sen 30°
3
1 2
1
1
3
tg 30° =
= 2 =
⋅
=
=
⋅
=
2 3
cos 30°
3
3
3
3
3
2
3
cos 30°
3 2
cotg 30° =
⋅
= 2 =
= 3.
1
sen 30°
2 1
2
3
=
4
3
.
2
α = 45 °
∆
Simmetrizzando il triangolo HOP rispetto al lato OP si ottiene il quadrato OHPH I .
2
Nota la diagonale del quadrato la misura del lato si ottiene con la formula: l =
d
2
2
2
2
2
Essendo la diagonale OP = 1 ⇒ OH =
OP =
⋅1 =
⇒ cos 45° =
.
2
2
2
2
y
HI
P
90°
45°
O
Inoltre sen 45° = PH = OH =
tg 45° =
sen 45°
1
=
= 1
cos 45°
1
Appunti di Matematica
45°
cos 45° H
45°
45°
A
O
x
2
.
2
cotg 45° =
P
45°
45°
90°
H
cos 45°
1
=
= 1
sen 45°
1
xoomer.virgilio.it/mimmocorrado
1
α = 60 °
∆
∆
Simmetrizzando il triangolo HOP rispetto al lato PH si ottiene il triangolo equilatero OPO I .
1
1
Essendo OP = 1 (raggio della circonferenza) ⇒ OH =
⇒ cos 60° = .
2
2
y
P
P
60°
sen 60°
60°
A
O cos 60° H
⎛1 ⎞
Inoltre sen 60° = ± 1 − cos 2 60° = + 1 − ⎜ ⎟
⎝2⎠
3
2 = 3 ⋅2 = 3 .
1
2 1
2
1
cos 60°
1 2
1
= 2 =
⋅
=
=
cot g 60° =
2 3
sen 60°
3
3
2
=
1−
1
60°
60°
O
x
2
1
1
=
4
3
=
4
H
3
=
4
OI
3
.
2
sen 60°
=
tg 60° =
cos 60°
Appunti di Matematica
1
3
⋅
=
3
3
xoomer.virgilio.it/mimmocorrado
3
.
3
2