Appunti di Matematica
Iperbole equilatera riferita agli asintoti
x2
y2
con a=b
− 2 = 1 =====⇒ x2 − y 2 = a2
2
a
b
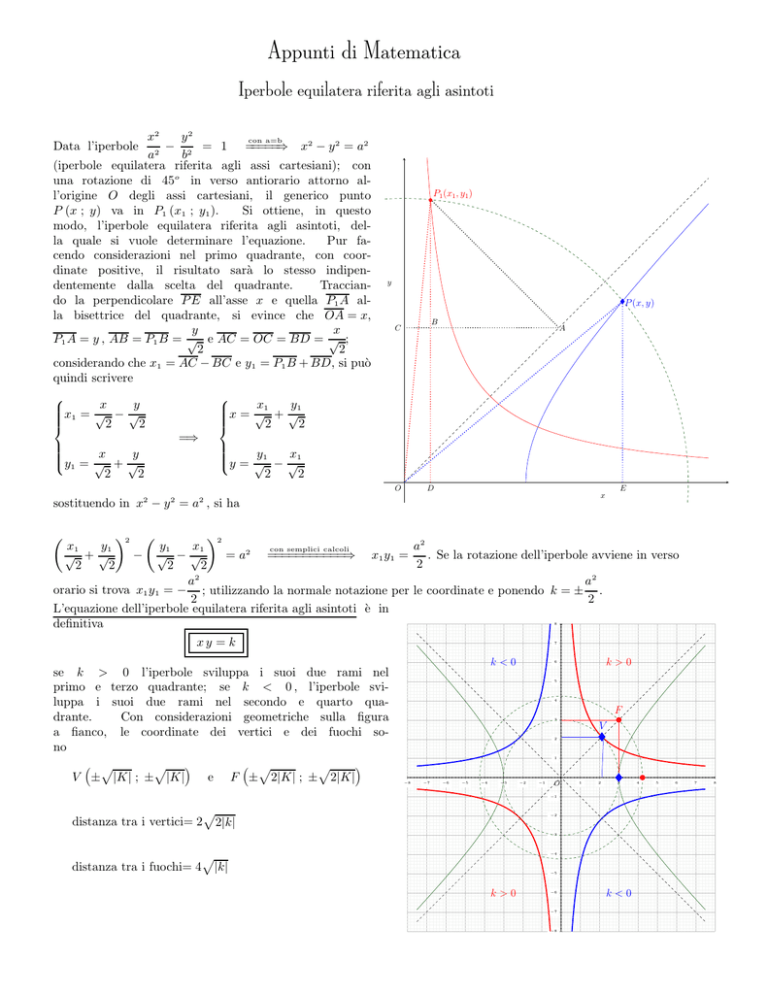
(iperbole equilatera riferita agli assi cartesiani); con
una rotazione di 45o in verso antiorario attorno all’origine O degli assi cartesiani, il generico punto
P (x ; y) va in P1 (x1 ; y1 ).
Si ottiene, in questo
modo, l’iperbole equilatera riferita agli asintoti, della quale si vuole determinare l’equazione.
Pur facendo considerazioni nel primo quadrante, con coordinate positive, il risultato sarà lo stesso indipendentemente dalla scelta del quadrante.
Tracciando la perpendicolare P E all’asse x e quella P1 A alla bisettrice del quadrante, si evince che OA = x,
y
x
P1 A = y , AB = P1 B = √ e AC = OC = BD = √ ;
2
2
considerando che x1 = AC − BC e y1 = P1 B + BD, si può
quindi scrivere
Data l’iperbole
x
y
x1 = √ − √
2
2
P1 (x1 , y1 )
y
P (x, y)
B
C
A
y1
x1
x= √ +√
2
2
=⇒
x
y
y1 = √ + √
2
2
x
y
y = √1 − √1
2
2
D
O
x
sostituendo in x − y = a , si ha
2
2
E
å2
y1
a2
x1
con semplici calcoli
− √ −√
= a2 ===========⇒ x1 y1 =
. Se la rotazione dell’iperbole avviene in verso
2
2
2
a2
a2
orario si trova x1 y1 = − ; utilizzando la normale notazione per le coordinate e ponendo k = ± .
2
2
L’equazione dell’iperbole equilatera riferita agli asintoti è in
definitiva
xy = k
Ç
y1
x1
√ +√
2
2
å2
2
Ç
8
7
se k > 0 l’iperbole sviluppa i suoi due rami nel
primo e terzo quadrante; se k < 0 , l’iperbole sviluppa i suoi due rami nel secondo e quarto quadrante.
Con considerazioni geometriche sulla figura
a fianco, le coordinate dei vertici e dei fuochi sono
Ä p
ä
Ä p
p ä
p
e F ± 2|K| ; ± 2|K|
V ± |K| ; ± |K|
distanza tra i vertici= 2
k<0
k>0
6
5
4
F
3
V
2
1
−8
−7
−6
−5
−4
−3
−2
−1
O
1
2
3
−1
p
2|k|
−2
−3
−4
distanza tra i fuochi= 4
p
|k|
−5
k>0
−6
−7
−8
k<0
4
5
6
7
8
C. Luviner
Iperbole equilatera riferita agli asintoti
2
Tangente all’iperbole equilatera, riferita agli asintoti, in un suo punto
Si vuole dimostrare che l’equazione della retta tangente ad un’iperbole equilatera, riferita agli asintoti, xy = k in
un suo punto P (α ; β) è αy + βx − 2k = 0 .
Si costruisce il sistema tra l’equazione di una generica retta y = mx + q e l’equazione dell’iperbole xy = k
e si pone uguale a zero il discriminante ∆ dell’equazione di secondo grado che da esso si ottiene (condizione di
tangenza),
xy = k
y = mx + q
=⇒
mx2 + qx − k = 0
=⇒
∆ = q 2 + 4mk = 0 (1) ;
dovendo il punto P appartenere sia all’iperbole che alla retta, si può scrivere
β = mα + q
(2)
e
αβ = k
(3) .
Sostituendo nell’equazione (1) la (3) e q 2 = (β − mα)2 , ottenuto dalla (2) , si ottiene, dopo semplici calcoli,
β
(β + mα)2 = 0 e quindi m = − e, sempre dalla (2), q = 2β .
α
β
Sostituendo i coefficienti m e q trovati nell’equazione y = mx + q si ha y = − x + 2β , da cui si ottiene
α
αy + βx − 2αβ = 0 , che, con la (3), diventa in definitiva:
αy + βx − 2k = 0 .
nota: nelle formule di sdoppiamento, il termine misto xy si sostituisce con
punto della curva
βx + αy
, con α e β coordinate del
2