Iperbole equilatera traslata
ax + b
dove i coefficienti a, b, c, d sono costanti assegnate e
cx + d
con c ≠ 0 rappresenta un’iperbole equilatera traslata avente:
La curva di equazione y =
d a
1. come centro di simmetria il punto O′ − ;
c c
d
a
2. come asintoti le rette x = − e y =
c
c
d a
Dimostrazione: basta operare una traslazione di assi che porti l’origine O in O′ − ; e
c c
ax + b
l’equazione y =
diventa del tipo XY = k .
cx + d
d a
In questo caso le formule di traslazione che portano O in O′ − ; sono:
c c
d
x = X − c
y = Y + a
c
Esempio: la curva di equazione y =
a=2
ha come coefficienti:
2x −1
−x +1
b = −1
c = −1 ( quindi c ≠ 0 )
d =1
Il centro di simmetria è:
d a
O′ − ; = (1; −2 )
c c
Gli asintoti sono le rette x = −
d
=1 e
c
a
= −2
c
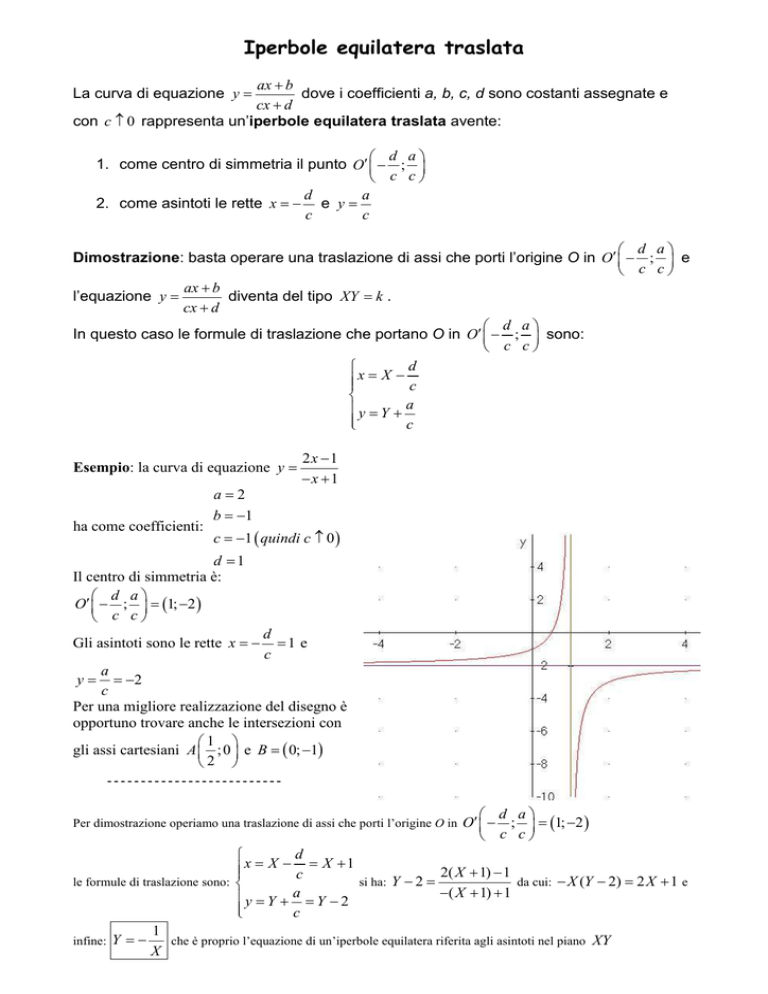
Per una migliore realizzazione del disegno è
opportuno trovare anche le intersezioni con
1
gli assi cartesiani A ; 0 e B = ( 0; −1)
2
y=
Per dimostrazione operiamo una traslazione di assi che porti l’origine O in
d a
O′ − ; = (1; −2 )
c c
d
x
=
X
−
= X +1
2( X + 1) − 1
c
si ha: Y − 2 =
da cui: − X (Y − 2) = 2 X + 1 e
le formule di traslazione sono:
a
−
(
X
+
1)
+
1
y = Y + = Y − 2
c
1
infine: Y = −
che è proprio l’equazione di un’iperbole equilatera riferita agli asintoti nel piano XY
X