trasformazioni termodinamiche

TRASFORMAZIONI TERMODINAMICHE – SISTEMI CHIUSI O SENZA DEFLUSSO –
Si fa riferimento alla massa unitaria (m = 1 kg) di un gas ideale e le trasformazioni sono quasi –
statiche; si suppone che il sistema termodinamico subisca una trasformazione che lo porta dallo
stato iniziale (stato 1) allo stato finale (stato 2).
Si ricorda che
la variazione di temperatura nella scala Kelvin coincide con la variazione di temperatura nella
scala Celsius
(T2 – T1) = (t1 – t2)
v1 V1
Il rapporto tra i volumi massici coincide con il rapporto tra i volumi
=
v 2 V2
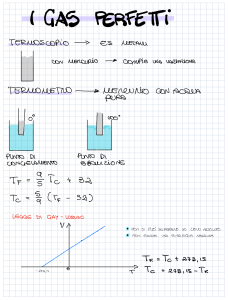
Trasformazione ISOCORA v = V = costante
p1 T1
=
legge di GAY - LUSSAC
p 2 T2
L=0
poichè ( v 2 − v1 ) = 0
Q = c V ⋅ (T2 − T1 )
Q = ∆U+L
J
kg
p
; Q = c V ⋅ (T2 − T1 )
(J)
2
p2
L=0
p1
Q=∆U
1
v
J
v1 ≡ v2
kg
Il calore somministrato al sistema provoca un aumento della pressione e della temperatura
(quindi dell’energia interna).
Il calore sottratto al sistema provoca un diminuzione della pressione e della temperatura (quindi
dell’energia interna).
La linea di trasformazione nel piano p-v è parallela all’asse delle ordinate.
∆ U = U2 − U1 = c V ⋅ (T2 − T1 )
•
•
•
Trasformazione ISOBARA p = costante
v1 T1
=
legge di GAY - LUSSAC
v 2 T2
L = p ⋅ ( v 2 − v1 )
Q = c p ⋅ (T2 − T1 )
J
kg
J
kg
; L = m ⋅ p ⋅ ( v 2 − v1 )
L = p ⋅ ( V2 − V1 )
(J)
(J)
; Q = m ⋅ c p ⋅ (T2 − T1 )
∆ U = U2 − U1 = c V ⋅ (T2 − T1 )
(J)
p
p1 ≡ p2
1
2
L
J
kg
v1
v2
v
Q = ∆U+L
c p ⋅ (T2 − T1 ) = c V ⋅ (T2 − T1 ) + p ⋅ ( v 2 − v1 )
c p ⋅ (T2 − T1 ) = c V ⋅ (T2 − T1 ) + R ⋅ (T2 − T1 )
•
•
•
cp − cV = R
Il calore somministrato al sistema provoca un aumento del volume e della temperatura (quindi
dell’energia interna).
Il calore sottratto al sistema provoca un diminuzione del volume e della temperatura (quindi
dell’energia interna).
La linea di trasformazione nel piano p-v è parallela all’asse delle ascisse.
Trasformazione ISOTERMA T = costante
p ⋅ v = cost. cioè p1 ⋅ v1 = p 2 ⋅ v 2
legge di BOYLE
v2
v2
L = p ⋅ dv = R ⋅ T ⋅
v1
dv
v
= R ⋅ T ⋅ ln 2
v
v1
v1
L = p1v1 ⋅ ln
v2
v1
J
kg
L = p 2 v 2 ⋅ ln
v2
v1
J
kg
∆ U = U2 − U1 = c V ⋅ (T2 − T1 ) = 0
p ⋅ v k = cost.
R ⋅T
p⋅
p
k
= cost.
con
R ⋅ T ⋅ v k -1 = cost.
k=
2
L
v1
v2
v
p
T k R k = cos t.
p
cV
T ⋅p
k
k
1− k
= cos t.
p
p1
1− k
k
k −1
J
kg
J
kg
2
L
v1
L = −c V ⋅ (T2 − T1 ) = c V ⋅ (T1 − T2 )
R ⋅ T1
v
L=
⋅ 1− 1
k −1
v2
Iperbole
p2
= cos t.
L = −∆ U
1
L=
⋅ ( p ⋅ v − p2 ⋅ v2 )
k −1 1 1
1
T k ⋅ k p1− k = k cos t.
T⋅p
Q = ∆U+L
cp
T ⋅ v k -1 = cost.
k
•
Iperbole
equilatera
p2
poichè T = cost.
Q=0
cioè p1 ⋅ v1k = p 2 ⋅ v 2k
p ⋅ v ⋅ v k -1 = cost.
•
1
Q=L
Trasformazione ADIABATICA
•
p
p1
J
kg
Se la pressione aumenta, il volume diminuisce (compressione)
Se la pressione diminuisce, il volume aumenta (espansione)
La linea di trasformazione nel piano p – v è un’iperbole equilatera
Q = ∆U+L
•
•
•
J
kg
v2
v
J
kg
p ⋅v
v
L = v 1 ⋅ 1− 1
k −1
v2
p ⋅v
p
L = v 1 ⋅ 1− 2
k −1
p1
k −1
k −1
k
J
kg
J
kg
Nell’espansione aumenta il volume mentre diminuiscono pressione e temperatura (quindi
l’energia interna).
Nella compressione diminuisce il volume mentre aumentano pressione e temperatura (quindi
l’energia interna).
La linea di trasformazione nel piano p – v è un’iperbole.