Ministero della Pubblica Istruzione
ISTITUTO STATALE DI ISTRUZIONE SUPERIORE
“Mariagrazia Mamoli”
Liceo delle Scienze Sociali
PROGRAMMAZIONE
ANNUALE
MATEMATICA con Elementi di STATISTICA
CLASSE TERZA
Indirizzo “ASCLEPIO” o Socio Sanitario
Indirizzo “LOGOS” o Della Comunicazione
Finalità e obiettivi di apprendimento generali
1) Promuovere le facoltà logiche ed intuitive per stabilire relazioni e cogliere analogie
differenze.
2) Educare gradualmente al processo di astrazione dei concetti.
3) Esercitare al ragionamento deduttivo ed induttivo.
4) Sviluppare le capacità analitiche e sintetiche.
5) Cogliere l’importanza di verificare la coerenza dei risultati
6) Consolidare l’utilizzo dei termini del linguaggio matematico educando gli alunni ad un rigore
espositivo sia sotto il profilo logico che sotto quello linguistico.
7) Esercitare ad interpretare, descrivere e rappresentare ogni fenomeno osservato.
8) Concorrere, con tutte le altre discipline del corso di studi, a sviluppare l’attitudine ad
affrontare con razionalità e capacità analitica situazioni e problemi di natura professionale e
di esperienza generale.
Obiettivi di apprendimento specifici
1) Consolidare ed approfondire la conoscenza dei concetti fondamentali di equazione e
disequazione; saper utilizzare con consapevolezza i principi di equivalenza per la risoluzione
di varie tipologie di equazioni e disequazioni di primo e secondo grado.
2) Consolidare ed approfondire la conoscenza del concetto di sistema di disequazioni; saper
risolvere sistemi di disequazioni.
3) Saper come si svolge un’indagine statistica e saperne rappresentare i dati.
4) Saper analizzare un insieme di dati statistici rappresentati graficamente
5) Saper utilizzare il metodo della geometria analitica per lo studio di luoghi geometrici nel
piano cartesiano.
6) Saper costruire il modello algebrico di semplici situazioni problematiche ed utilizzare poi gli
strumenti algebrici a disposizione per la loro risoluzione.
Competenze di base
Di seguito le competenze di base previste al termine del corso di studi, definite in sede di
programmazione di Dipartimento ed al cui raggiungimento concorrono gli obiettivi dettagliati
riportati nel seguito della programmazione con gli opportuni riferimenti (C1, C2, C3, C4).
C1) Comprendere il messaggio scritto e/o verbale (testo, fenomeno, problema) all’interno del
processo comunicativo individuando i punti fondamentali dell’informazione.
C2) Potenziare le modalità logiche di apprendimento: analizzare, selezionare dati, confrontare
(fatti, dati, termini…), costruire relazioni, giustificare e trarre conclusioni.
C3) Individuare forme e strumenti di espressione (modelli interpretativi) per trasmettere un
messaggio (grafico, simbolico, naturale…) acquisendo capacità di mobilità dall’una
all’altra
C4) Individuare problemi e proporre soluzioni. Riflettere sui procedimenti applicandoli in
diversi contesti operativi e valutarne i risultati.
ISIS “MAMOLI” - Programmazione annuale Matematica con elementi di Statistica - Classe Terza
1/7
Moduli fondamentali previsti per la classe terza
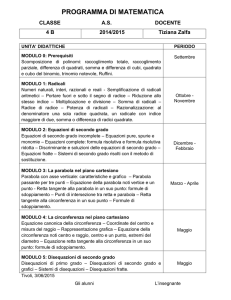
Modulo n° 1 – Equazioni e Disequazioni. (Settembre/Novembre)
Conoscenze
Classificare le equazioni e le disequazioni secondo il grado e il numero delle incognite.
Illustrare i metodi per risolvere varie tipologie di equazioni e disequazioni sino a quelle
irrazionali e/o con valori assoluti.
Competenze
Risolvere varie tipologie di equazioni e disequazioni (comprese le frazionarie e quelle di
grado superiore al secondo) sino ad alcune semplici irrazionali e/o con valori assoluti. (C3,
C4)
Contenuti fondamentali
Richiami sulle disequazioni intere di primo grado.
Richiami sulle equazioni di secondo grado e sulle equazioni di grado superiore al secondo.
Disequazioni intere di secondo grado e di grado superiore al secondo.
Disequazioni frazionarie.
Sistemi di disequazioni.
Equazioni irrazionali riconducibili alle forme A( x) B( x) , 3 A( x) B( x) .
Disequazioni irrazionali riconducibili alle forme
n
A( x) B( x) ,
n
A( x) B( x) .
Equazioni con valori assoluti riconducibili alle forme A( x) k , A( x) B( x) , A( x) B( x)
Disequazioni con valori assoluti riconducibili alle forme A( x) k , A( x) k , con k numero
reale
Semplici problemi che hanno come modello disequazioni
Modulo n° 2 – Il piano cartesiano e la retta (Dicembre/Febbraio)
Conoscenze
Enunciare le formule del punto medio di un segmento, della distanza tra due punti e della
distanza di un punto da una retta.
Illustrare qual è l’equazione di una retta e quali sono le sue caratteristiche
Competenze
Determinare il punto medio di un segmento, la distanza tra due punti e la distanza di un
punto da una retta. (C3, C4)
Determinare l’intersezione tra due rette (C3, C4)
Scrivere l’equazione di una retta note particolari condizioni (passaggio per un punto,
parallelismo, perpendicolarità) (C2, C3, C4)
Contenuti fondamentali
Piano cartesiano
Distanza tra due punti - Punto medio di un segmento
Equazione della retta nel piano cartesiano
Rette parallele e posizione reciproca di due rette - Rette perpendicolari
Determinazione dell’equazione di una retta
Distanza di un punto da una retta
Fasci di rette
ISIS “MAMOLI” - Programmazione annuale Matematica con elementi di Statistica - Classe Terza
2/7
Modulo n° 3 – La circonferenza (Marzo/Aprile).
Conoscenze
Conoscere l’equazione e il grafico di una circonferenza
Conoscere le condizioni di tangenza di una retta ad una circonferenza
Competenze
Determinare l’intersezione tra una retta ed una circonferenza (C3, C4)
Scrivere l’equazione di una circonferenza note particolari condizioni (passaggio per un
punto, coordinate del centro, raggio, …) (C3, C4)
Utilizzare la condizione di tangenza di una retta ad una circonferenza. (C1, C2, C3, C4)
Contenuti fondamentali
Equazione della circonferenza
Circonferenza e retta
Determinazione dell’equazione di una circonferenza
Modulo n° 4 – La parabola (Aprile/Maggio)
Conoscenze
Conoscere l’equazione e il grafico di una parabola
Conoscere le condizioni di tangenza di una retta ad una parabola
Competenze
Determinare l’intersezione tra una retta ed una parabola e tra parabole (C3, C4)
Scrivere l’equazione di una parabola note particolari condizioni (passaggio per un punto,
coordinate del fuoco, direttrice, …) (C3, C4)
Utilizzare la condizione di tangenza di una retta ad una parabola (C1, C2, C3, C4).
Contenuti fondamentali
Parabola con vertice nell’origine
Parabola con asse parallelo a uno degli assi cartesiani
Parabola e retta
Determinazione dell’equazione di una parabola
Modulo n° 5 – L’indagine statistica e le sue fasi (Giugno)
Conoscenze
Conoscere il significato dei dati statistici e delle varie rappresentazioni grafiche
Conoscere le definizioni degli indici di posizione e di variabilità.
Conoscere il significato dei rapporti statistici
Competenze
Saper calcolare la media, la moda e la mediana di un insieme di dati (C3, C4)
Saper calcolare lo scarto quadratico medio (C3, C4)
Saper come si svolge un’indagine statistica e saperne rappresentare i dati (C1, C2, C3, C4)
Saper analizzare un insieme di dati rappresentati graficamente (C1, C2)
Contenuti fondamentali
Dati statistici (Popolazione, carattere, modalità, tabelle di frequenza)
Rappresentazione grafica dei dati
Indici di posizione centrale (Media aritmetica, geometrica, armonica e quadratica; mediana e
moda
Indici di variabilità (Campo di variazione, scarto semplice medio, scarto quadratico medio,
distribuzione gaussiana, coefficiente di variazione, concentrazione)
Rapporti statistici
ISIS “MAMOLI” - Programmazione annuale Matematica con elementi di Statistica - Classe Terza
3/7
Indicazioni metodologiche
Si fa presente che nella classe terza la struttura oraria prevede solo tre ore settimanali per questa
disciplina e pertanto, ferme restando le indicazioni metodologiche di seguito esposte, sarà
fondamentale per un proficuo apprendimento la maturazione da parte degli alunni di un metodo
di studio personale ed autonomo; infatti i tempi per l’attività di consolidamento/recupero con
l’insegnante saranno inevitabilmente ridotti.
Fondamentale sarà anche l’utilizzo sistematico da parte degli alunni del libro di testo, sia per lo
studio teorico degli argomenti, sia per lo svolgimento di esercitazioni a casa.
Convinti che ciò che qualifica l’attività matematica è il porre e risolvere problemi si cercherà di
evitare di assegnare esclusivamente esercizi di tipo ripetitivo, pur consapevoli che il loro
sviluppo è necessario in alcune fasi importanti dell’apprendimento (per esempio dove sia
necessario recuperare abilità tecniche di calcolo).
In generale, nello sviluppo dell’attività didattica, si terrà conto delle seguenti indicazioni:
- occorre chiarire la differenza tra i concetti e gli strumenti che li rappresentano;
- lo studio dei concetti deve sempre essere condotto nei due sensi possibili: verso il problema
e verso la loro formalizzazione; questo per riflettere sia sui campi di applicazione e i
problemi che si possono risolvere, sia sulle motivazioni che stanno alla base delle stesse
tecniche di calcolo;
- utilizzare immediatamente i concetti al fine di mostrare l’utilità degli strumenti matematici
presentati;
- passare dall’uno all’altro tra i differenti temi trattati.
I metodi che si utilizzeranno nell’esame dei contenuti e per il raggiungimento degli obiettivi
prefissati saranno:
- lezione frontale;
- lezione dialogata;
- metodo della scoperta guidata;
- momenti di consolidamento e recupero.
Le fasi del lavoro svolto in classe saranno indicativamente così suddivise:
- esporre le ragioni e gli obiettivi dell’attività che ci si appresta a svolgere;
- fornire gli strumenti indispensabili all’approccio dell’argomento;
- stimolare l’intuizione e la scoperta di proprietà, di analogie e differenze;
- valutare immediatamente le idee, anche attraverso la loro applicazione;
- sistemare organicamente le idee;
- valutare il raggiungimento degli obiettivi;
- effettuare un’opera di revisione nel caso in cui l’assimilazione dei contenuti essenziali non
raggiunga un livello adeguato.
Lavoro a casa degli studenti
Il lavoro a casa dello studente consisterà nella sistemazione e nel consolidamento dei concetti
affrontati in classe e dovrà essere conseguente ad ogni lezione e precedente alla successiva.
Gli esercizi assegnati per compito a casa dall’insegnante rientrano in questo lavoro e potranno
essere lo spunto per chiarimenti e approfondimenti; il numero degli esercizi assegnati varierà a
seconda dell’argomento, in modo tale che il loro svolgimento sia il più possibile ragionato e non
sempre meccanico; in ogni caso si cercherà di evitare che l’impegno risulti eccessivamente
gravoso per lo studente.
Soprattutto nella fase finale dello svolgimento di una unità didattica, lo studente dovrà effettuare
uno studio globale che sarà oggetto di verifica scritta e possibilmente anche orale.
ISIS “MAMOLI” - Programmazione annuale Matematica con elementi di Statistica - Classe Terza
4/7
Si sottolinea infine l’importanza dell’uso sistematico del libro di testo in adozione, che
rappresenta il supporto fondamentale di tutta l’attività svolta a casa dallo studente.
Attività di verifica
La verifica formativa sarà una verifica in itinere mediante il colloquio insegnante-alunno,
formulazione di schemi, esercitazioni sul quaderno e alla lavagna, interventi dal posto,
correzione dei compiti assegnati, brevi interrogazioni.
La verifica sommativa avverrà al termine di ciascuna unità didattica ( o parte di essa ) mediante
lo svolgimento di una prova scritta che potrà essere composta da esercizi aperti, quesiti a risposta
multipla, scelte vero/falso a seconda delle abilità che si vogliono testare.
Verranno svolte almeno due verifiche scritte e due orali nel primo quadrimestre, e tre verifiche
scritte e due orali nel secondo quadrimestre; una delle verifiche orali quadrimestrali potrà essere
effettuata mediante prova scritta “valida per l’orale”. Le valutazioni saranno riportate
sull’apposito libretto e dovranno essere firmate dai genitori dell’alunno.
Attività di valutazione
Per le prove scritte si procederà assegnando un punteggio ad ogni esercizio e stabilendo quindi
delle fasce di punteggi; a ciascuna fascia corrisponderà un voto (partendo dalla valutazione
massima che sarà dieci a quella minima che sarà uno); in particolare la fascia della sufficienza
verrà individuata sommando i punteggi relativi agli esercizi la cui corretta risoluzione si riterrà
irrinunciabile per il conseguimento degli obiettivi cognitivi minimi coinvolti nella verifica,
questa somma si attesterà intorno al 60% del punteggio totale. La suddivisione in fasce e la
relativa valutazione sarà sempre resa esplicita agli alunni così come il punteggio assegnato ad
ogni singolo esercizio.
Le interrogazioni orali saranno volte a valutare, oltre le abilità operative acquisite, anche la
capacità di ragionamento e la chiarezza espositiva maturata.
Per la valutazione curriculare ci si atterrà agli indicatori ed ai descrittori della griglia allegata.
Nella valutazione finale si terrà conto del raggiungimento (riscontrabile nelle verifiche svolte
durante tutto l’anno) degli obiettivi minimi in merito alla conoscenza dei contenuti ed alle abilità
acquisite, della progressione dei risultati rispetto alla situazione di partenza, dell’impegno e
dell’assiduità dimostrati nello studio e nel lavoro a casa, nonché di una eventuale partecipazione
alle attività di recupero. Per le modalità e i criteri di presentazione agli scrutini di fine anno si
farà comunque riferimento a quanto verrà deliberato a livello di Collegio Docenti e di Consiglio
di Classe nel corso dell’anno scolastico.
ISIS “MAMOLI” - Programmazione annuale Matematica con elementi di Statistica - Classe Terza
5/7
Criteri di valutazione
VOTO
10
15
CONOSCENZE
30
Possiede una conoscenza completa,
coordinata, approfondita e ampliata degli
argomenti, delle informazioni e dei termini
specifici.
Espone i contenuti in modo preciso, chiaro
e completo.
Possiede una conoscenza completa,
coordinata, approfondita degli argomenti,
delle informazioni e dei termini specifici.
Espone i contenuti con grande fluidità e
ricchezza verbale
Possiede una conoscenza completa, e
approfondita degli argomenti, delle
informazioni e dei termini specifici.
Espone i contenuti in modo preciso, in
forma comprensibile e articolata.
Possiede una conoscenza completa, e
approfondita degli argomenti, delle
informazioni e dei termini specifici.
Espone i contenuti con precisione, in forma
comprensibile e argomentata.
Dimostra di possedere le conoscenze
essenziali degli argomenti, delle
informazioni, dei termini specifici.
Espone i contenuti con accettabile
correttezza e in forma comprensibile.
Se guidato, riesce a fornire chiarimenti,
precisazioni, completamenti
Dimostra di avere studiato, ma di non aver
conseguito una sufficiente assimilazione.
Espone i contenuti con qualche
imprecisione e travisamento, in forma non
sempre logica e comprensibile.
14
29
28
8
13
27
26
7
12
11
6
10
21
20
5
9
8
19
18
17
16
4
7
6
15
14
13
12
Dimostra di non conoscere gli argomenti.
Espone i contenuti con lacune ed errori.
L’argomentazione è confusa ed incerta.
3
5
4
11
10
9
8
Dimostra studio molto scarso.
Espone i contenuti con gravi lacune ed
errori, in forma disordinata e poco chiara.
2
3
2
7
6
5
4
Dimostra studio pressoché nullo.
Espone soltanto frammenti di contenuto,
per sentito dire o per intuito.
1
1
3
2
1
Non svolge le prove scritte e si rifiuta di
sostenere le prove orali
9
25
24
23
22
COMPETENZE
ABILITA’
Lavora in autonomia, organizza
il proprio lavoro, utilizza le
tecniche appropriate, opera con
grande precisione e originalità.
Risolve correttamente i
problemi con procedure logiche
e chiare, senza alcun errore
Lavora in autonomia, organizza
il proprio lavoro, utilizza le
tecniche appropriate, opera con
grande precisione e originalità.
Risolve correttamente i
problemi con procedure logiche
e chiare, errori e imprecisioni
riguardano solo aspetti
marginali
Lavora in autonomia, organizza
il proprio lavoro, utilizza le
tecniche appropriate, opera con
precisione.
Risolve correttamente i
problemi con procedure valide,
anche se a volte si notano sviste
o incompletezza.
Sa utilizzare le tecniche
appropriate e opera con
precisione anche se non sempre
in completa autonomia.
Esegue con correttezza le
procedure apprese e opera con
accettabile precisione.
Risolve correttamente i
problemi con procedure valide,
anche se a volte si notano
sviste, travisamenti o
incompletezza.
Incontra difficoltà
nell’applicazione delle
conoscenze. Risolve i problemi
con procedure valide,
emergono alcune incertezze; i
passaggi più difficili non
vengono superati.
Ha bisogno di essere guidato o
di imitare; solo così riesce ad
ottenere risultati accettabili.
Nei problemi commette errori
di procedura o non ne trova una
valida, ciò, a volte, anche su
argomenti essenziali.
Denota disimpegno e ignoranza
delle metodiche.
Opera in modo impreciso.
Nei problemi commette
numerosi errori anche gravi,
dimostrando, spesso, di non
possedere procedure risolutive.
Denota disimpegno e ignoranza
delle metodiche.
Opera in modo gravemente
impreciso e a volte costituisce
disturbo per gli altri.
Denota disimpegno e ignoranza
delle metodiche.
Opera in modo gravemente
impreciso, costituisce disturbo
per gli altri.
Non lavora e disturba gli altri
Nei problemi commette
numerosi errori anche gravi,
dimostrando di non possedere
procedure risolutive.
Non sa risolvere i problemi.
Non svolge le prove
ISIS “MAMOLI” - Programmazione annuale Matematica con elementi di Statistica - Classe Terza
6/7