Problema Torre 1 - Europa Digital School

Calcolare l’altezza di una torre (o di un albero, o di un’antenna, ecc..) AB il cui
piede appoggia sul piano orizzontale ove opera l’osservatore
Per questo tipo di problema dobbiamo distinguere due casi, a seconda che il piede A
della torre sia accessibile oppure no.
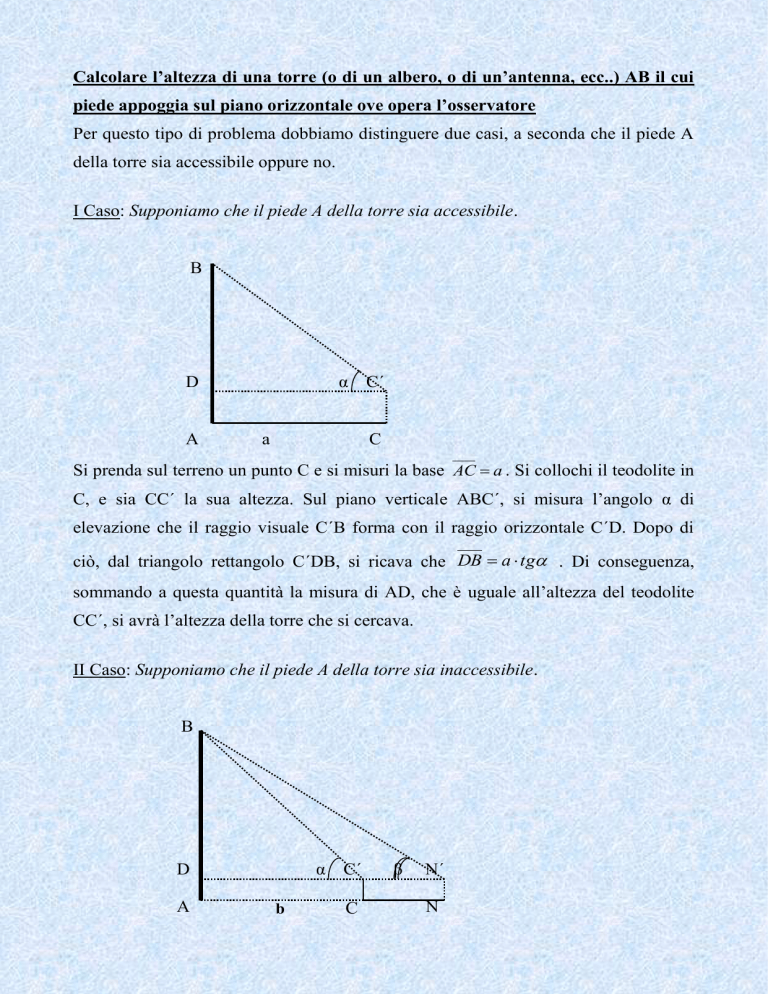
I Caso: Supponiamo che il piede A della torre sia accessibile.
B
α C΄
D
A
a
C
Si prenda sul terreno un punto C e si misuri la base AC  a . Si collochi il teodolite in
C, e sia CC΄ la sua altezza. Sul piano verticale ABC΄, si misura l’angolo α di
elevazione che il raggio visuale C΄B forma con il raggio orizzontale C΄D. Dopo di
ciò, dal triangolo rettangolo C΄DB, si ricava che DB  a  tg . Di conseguenza,
sommando a questa quantità la misura di AD, che è uguale all’altezza del teodolite
CC΄, si avrà l’altezza della torre che si cercava.
II Caso: Supponiamo che il piede A della torre sia inaccessibile.
B
D
A
α C΄
b
C
β
N΄
N
In questo caso si misura direttamente sul terreno una base CN  b , allineata con A,
cioè giacente nel piano verticale della visuale AB. Poi, posto il teodolite, una volta in
C, e una volta in N, si misureranno gli angoli DCˆ B   e DNˆ B   , essendo
CC΄=NN΄ l’altezza del teodolite. Dopo questa premessa, essendo N Cˆ B  180   e
N Bˆ C      , dal triangolo DBC΄, si ha che
(1)
DB  CB sen ,
mentre, dal triangolo C΄BN΄, per il teorema dei seni, si ottiene che
bsen
C B
b

da cui C B 
.
sen   
sen sen   
Sostituendo questo valore al posto di C B nella (1), si ha che DB 
b  sen  sen
.
sen   
Aggiungendo a questa quantità l’altezza AD dello strumento, si ottiene la misura
cercata della torre AB.