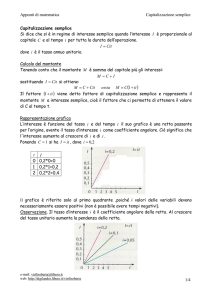
VERIFICA DI MATEMATICA
CL. ………………………
Matematica finanziaria
COGNOME _____________________
DATA____________
NOME____________________
A) CAPITALIZZAZIONE SEMPLICE
1)
Vero o Falso ?
a)
il montante è direttamente proporzionale al capitale, a parità di tempo e di tasso __________
b)
il capitale deve essere sempre maggiore dell’interesse, qualunque sia il valore di t (tempo di
impiego)
___________
c)
il tasso di interesse semestrale è doppio di quello annuo corrispondente _________________
d)
per il calcolo dell’interesse bisogna sempre usare il tasso annuo _____________
e)
il montante, qualunque sia t ≥0, è sempre maggiore del capitale
f)
l’interesse, a parità di tasso e capitale, è direttamente proporzionale al tempo _____________
g)
i grafici dell’interesse e del montante sono:
h)
una retta e una curva esponenziale _________
due rette parallele ___________
due rette incidenti ___________
______________
per il calcolo dell’interesse, per periodi inferiori all’anno, si deve:
usare il tasso annuo _________
trasformare il tempo in anni _________
esprimere il tempo in unità di misura coerenti con il periodo a cui si è
riferito il tasso__________
B) CAPITALIZZAZIONE COMPOSTA
1) Vero o Falso?
a)
a parità di capitale, tasso e tempo, il montante per tempi inferiori ad un periodo, rispetto a
quello in capitalizzazione semplice, è:
b)
maggiore _____________
minore _______________
uguale _______________
per un deposito di durata pari ad un anno:
il montante di una lira al 3% semestrale equivale al montante di una lira al 6%
annuo__________
il montante di una lira all’8% annuo convertibile trimestralmente, è pari al montante di
una lira al 2% trimestrale ______________
c)
l’interesse viene pagato : (attenzione!!!!!pagato non calcolato)
alla fine di ciascun anno ___________
alla fine di ciascun periodo di capitalizzazione _______________
insieme al capitale alla scadenza del deposito dopo aver fruttato a sua volta
interessi __________
d)
se i = 0,14
allora
i2 =
0,07
0,076 ____________
0,067 ____________
0,071 ____________
____________
e)
se C = 6.800.000 ; M = 18.944.545 ; t = 21 semestri
allora
i2 =
0,045 ____________
0,05
0,055 ____________
0,06
____________
____________
C) CAPITALIZZAZIONE E SCONTO (TEST MISTO: le risposte non dipendono dal regime di
capitalizzazione ma sono uguali comunque a meno che il regime di capitalizzazione venga
nominato esplicitamente)
1) Vero o falso?
a)
il valore di un capitale C varia al variare dell’epoca in cui esso si rende esigibile _________
b)
due somme di diversa entità non possono mai essere considerate equivalenti dal punto di vista
finanziario _______________(attenzione!!!!!!pensa!!!!!!)
c)
il modello grafico della capitalizzazione semplice è una retta ________________
d)
due tassi sono equivalenti se sono identici _______________
e)
lo sconto è la somma che spetta a chi paga prima della scadenza_________________
f)
il valore nominale di un titolo è il valore indicato sul titolo ________________
2) Completare inserendo al posto dei puntini le parole scelte correttamente fra le seguenti
( sconto, tasso, tempo, valore attuale, semplice, montante, interesse, somma scontata)
a)
_________________________è il valore di una somma S di cui si anticipa il pagamento
b)
il compenso che spetta a chi anticipa un pagamento è detto _________________
c)
il valore di una somma
S calcolato in un’epoca anteriore alla sua scadenza è detta
anche_____________________
d)
il ____________________è la somma del capitale più __________________maturato
e)
in regime di capitalizzazione _____________l’interesse prodotto da un capitale non è fruttifero
f)
per il calcolo dell’interesse ____________e______________devono essere espresse nella
stessa unità di misura
3) Il seguente grafico rappresenta l’andamento di un investimento nell’arco di un semestre.
Stabilire quale delle seguenti affermazioni è corretta.
Valore di un investimemnto
700
milioni di lire
600
500
400
300
200
100
0
0
1
2
3
4
5
6
7
mesi
l’intervallo di massima crescita per l’investimento è 4 < t <5
nell’intervallo 0 < t < 3 il capitale rimane costante
la massima crescita si ha nell’intervallo 5 < t < 6
nell’arco del semestre il rendimento è sempre costante
nell’arco del semestre il rendimento è non decrescente
4) In regime di capitalizzazione composta, quale tra le seguenti formule esprime
l’equivalenza
5) Se
tra due tassi diversamente frazionati?
i h = 1 - ( 1+i k)h / k
i h = ( 1+i k)k / h - 1
i h = ( 1+i k)1 / k
i h = 1 - ( 1+i k)k / h
(1+ih)k = (1+ik)h
2C = C ( 1+i )t quanto vale t ?
log 2 – log (1+i )
log (1+i ) – log 2
log 2 / log (1+i )
log [2 / (1+i )]
log [( 1 + i ) / 2 ]
6) Sull’asse dei tempi è rappresentata un’operazione finanziaria complessa che prevede un
capitale C1 esigibile oggi, un capitale C2 esigibile fra 4 anni e un capitale C3 esigibile fra 7
anni.
C1
|
C2
|
|
0
|
|
C3
|
|
|
4
t
7
Quale delle formule sottoscritte rappresenta il valore al tempo 4 dell’intera operazione?
V = C1(1+i)-4 + C2 + C3(1+i)3
V = C1(1+i)4 + C2 + C3(1+i)-3
V = C1(1+i)-4 + C2 + C3(1+i)-3
V = C1(1+i)4 + C2 + C3(1+i)3
V = C1(1+i)-4 + C2(1+i) + C3
D) RENDITE
1) Completa il seguente organigramma
RENDITE
DURATA
DECORRENZA
SCADENZA RATA
2) Vero o falso?
a)
valutare una rendita significa determinare un unico capitale equivalente al valore di tutte le
rate in una prefissata epoca ________________
b)
il valore attuale di una rendita perpetua anticipata è dato da V =
c)
una rendita è una successione di capitali esigibili in prefissate epoche ___________________
d)
il valore attuale di una rendita è calcolato in un’epoca precedente tutte le scadenze
____________
e)
il montante di una rendita è una valutazione fatta in un momento qualsiasi della sua
durata______
R
i
____________
3) Completa
a)
stipendi e salari sono esempi di rendite _______________________
b)
l’interesse maturato dai BOT è un esempi di rendita_______________
c)
in un regime di capitalizzazione composta, le rendite a rate costanti costituiscono una
progressione __________________ di ragione_________________
d)
R•
e)
in riferimento ad una rendita
_________________________
0
|
1- (1+ i) -n
i
è la formula che calcola il ___________________
perpetua,
4) Il seguente grafico rappresenta una rendita.
1
2
3
4
5
6
7
|
|
|
|
|
|
|
R
R
R
R
R
ha
senso
solo
il
calcolo
del
8
|
R
Descrivila qui sotto
Si tratta di una rendita______________________________________________________________
________________________________________________________________________________
E) EQUIVALENZA FINANZIARIA
Impostare l’equazione che risolve il seguente problema:
“ Dieci anni fa, Tizio ha contratto un debito di £. 5.000.000 che avrebbe dovuto rimborsare
oggi al tasso del 12% annuo. Non avendo disponibilità finanziarie, chiede al suo creditore di
poter versare, invece del dovuto, un capitale C fra due anni, un capitale doppio del precedente
fra quattro anni e un capitale uguale al primo fra cinque anni. Facendo i calcoli sempre al
12% annuo, impostare l’equazione che risolve il problema.
(Se si vuole si può anche risolvere l’equazione e trovare il valore dei tre capitali)