Appunti di matematica
Capitalizzazione semplice
Capitalizzazione semplice
Si dice che si è in regime di interesse semplice quando l’interesse I è proporzionale al
capitale C e al tempo t per tutta la durata dell’operazione.
I = Cit
dove i è il tasso annuo unitario.
Calcolo del montante
Tenendo conto che il montante M è somma del capitale più gli interessi:
M =C+I
sostituendo I = Cit si ottiene:
M = C + Cit
ossia M = C (1 + it )
Il fattore (1 + it ) viene detto fattore di capitalizzazione semplice e rappresenta il
montante M a interesse semplice, cioè il fattore che ci permette di ottenere il valore
di C al tempo t.
Rappresentazione grafica
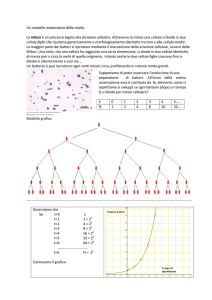
L’interesse è funzione del tasso i e del tempo t il suo grafico è una retta passante
per l’origine, avente il tasso d’interesse i come coefficiente angolare. Ciò significa che
l'interesse aumenta al crescere di i e di t .
Ponendo C = 1 si ha I = it , dove i = 0,2
t I
0 0,2*0=0
1 0,2*1=0,2
2 0,2*2=0,4
Il grafico è riferito solo al primo quadrante ,poiché i valori delle variabili devono
necessariamente essere positivi (non è possibile avere tempi negativi).
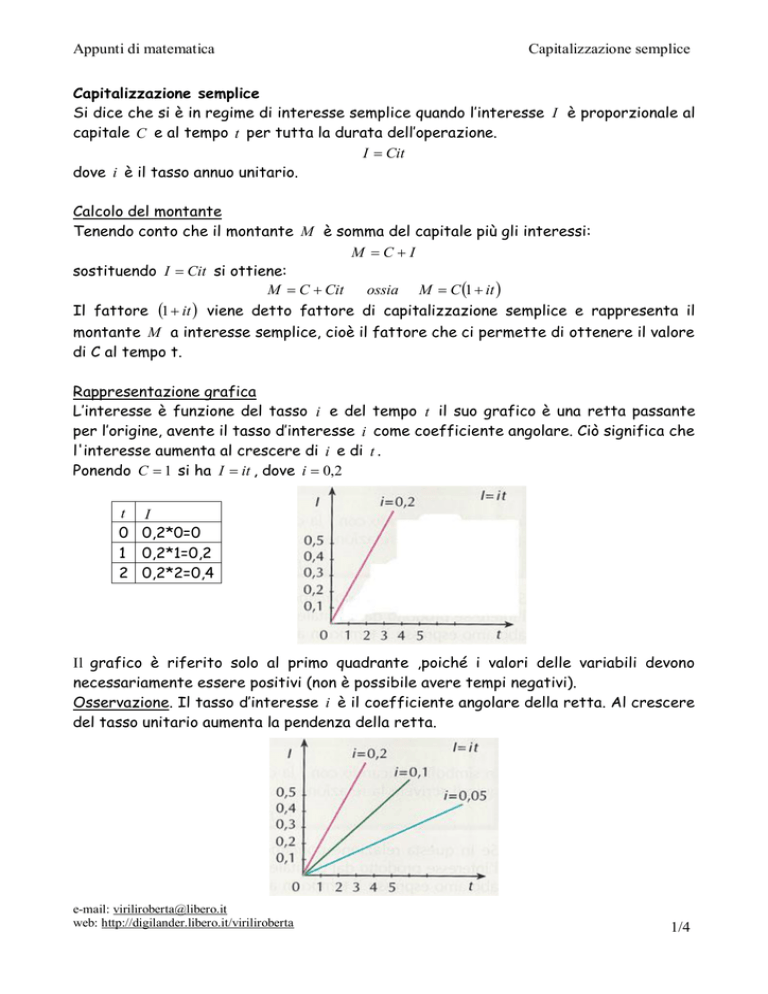
Osservazione. Il tasso d’interesse i è il coefficiente angolare della retta. Al crescere
del tasso unitario aumenta la pendenza della retta.
e-mail: [email protected]
web: http://digilander.libero.it/viriliroberta
1/4
Appunti di matematica
Capitalizzazione semplice
Il montante M gode della proprietà di essere una funzione lineare del tempo.
Graficamente il fattore di montante a interesse semplice è rappresentato dalla
semiretta che esce dal punto (0,1), giace nel primo quadrante ed è caratterizzata da
pendenza espressa dal coefficiente angolare i (non negativo).
Osservazione. Le due funzioni I = it e M = 1 + it , avendo lo stesso coefficiente
angolare i , rappresentano per t ≥ 0 , due semirette parallele.
Esempio 1
Calcolare l’interesse semplice di un capitale di € 2000 impiegato al 5 % annuo per 1
anno e 3 mesi.
Svolgimento
Dati: C = 2000 ; i = 5% =
5
= 0,05 ; t = 1 anno e 3 mesi
100
•
Trasformare il tasso percentuale I = 5/100 = 0.05 ed il tempo in anni :
•
Calcolare infine l’interesse:
L’interesse è di € 125 .
e-mail: [email protected]
web: http://digilander.libero.it/viriliroberta
2/4
Appunti di matematica
Capitalizzazione semplice
Esempio 2
Sette anni fa, è stata impiegata la somma di € 5000 al tasso del 6 % e dopo un certo
periodo, la somma di € 4000 al tasso del 7,5 %. Sapendo che oggi il montante
complessivo è di €12000, calcolare dopo quanto tempo è stato effettuato il secondo
versamento.
Svolgimento
Se si indica con t il tempo in cui è avvenuto il secondo versamento, risulta:
5000 ( 1 + 0.06*7 ) + 4000 (1 + 0.075*t ) = 12000
Si ottiene una equazione di primo grado in cui la variabile è t.
5000(1 + 0,42) + 4000(1 + 0,075 ⋅ t ) = 12000
7100 + 4000(1 + 0,075 ⋅ t ) = 12000
4000(1 + 0,075 ⋅ t ) = 12000 − 7100
4000(1 + 0,075 ⋅ t ) = 4900
(1 + 0,075 ⋅ t ) = 4900
4000
(1 + 0,075 ⋅ t ) = 1,225
0,075 ⋅ t = 1,225 − 1
0,075 ⋅ t = 0,225 ⇒
t=
0, 225
=3
0,075
Quindi il secondo versamento è stato effettuato 3 anni dopo il primo.
Esempio 3
Dopo quanto tempo, in regime di capitalizzazione semplice, i montanti di due capitali,
rispettivamente di € 7000 impiegati al 5% e di € 6500 impiegati al 6%, risulteranno
eguali ?
e-mail: [email protected]
web: http://digilander.libero.it/viriliroberta
3/4
Appunti di matematica
Capitalizzazione semplice
Svolgimento
Indicando con M1 il montante prodotto dal primo capitale e con M2 il montante
prodotto dal secondo capitale, risulta:
M1 = M2
7000 (1 + 0.05 * t ) = 6500 (1 + 0,06 * t )
7000 + 350 * t = 6500 + 390 * t
40 * t = 500
t = 12,5.
t = 12 anni e 6 mesi.
Esempio 4
Calcolare l’interesse semplice prodotto in 2 anni e 2 mesi da un capitale di € 4000 al
tasso annuo del 3%.
Svolgimento
•
Trasformare il tempo che deve essere espresso in anni:
2 13
t =2+
=
12 6
•
Applicare la formula I = Cit per calcolare l’interesse
13
I = 4000 ⋅ 0,03 ⋅ = 260 €
6
Esempio 5
Calcolare l’interesse semplice ed il montante del capitale di € 8000 impiegato per 5
mesi al tasso annuo del 6%.
Svolgimento
•
Trasformare il tempo che deve essere espresso in anni:
5
t = 5 mesi =
di anno
12
•
Applicare la formula I = Cit per calcolare l’interesse
5
I = 8000 ⋅ 0,06 ⋅ = 200 €
12
Applicare la formula I = Cit per calcolare l’interesse
•
M = C + I = 8000 + 200 = 8200 €
•
e-mail: [email protected]
web: http://digilander.libero.it/viriliroberta
4/4