Iperbole - Virgilio

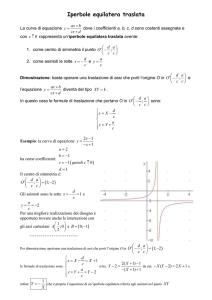
Iperbole a centro ( F1 , F2  Asse x )
x2 y 2

1
a2 b2
L’equazione dell’iperbole a centro con i fuochi sull’asse delle x è :
y
Asse trasverso = 2 a
Asse non trasverso = 2 b
Distanza focale = 2 c
c
Eccentricità e 
a
c 2  a 2  b2
b
Asintoti y   x
a
V3(0,b)
c
b
a
V1(a,0)
F2(-c,0)
V2(-a,0)
F1(c,0)
x
V4(0,-b)
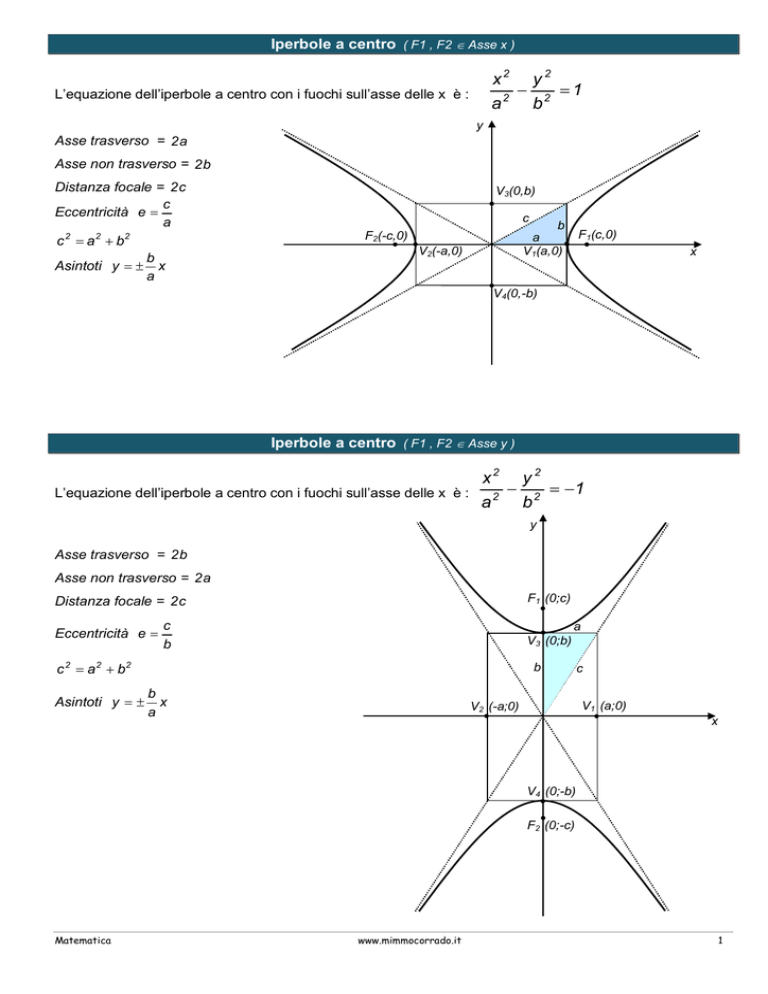
Iperbole a centro ( F1 , F2  Asse y )
L’equazione dell’iperbole a centro con i fuochi sull’asse delle x è :
x2 y 2

 1
a2 b2
y
Asse trasverso = 2 b
Asse non trasverso = 2 a
F1 (0;c)
Distanza focale = 2 c
Eccentricità e 
c
b
a
V3 (0;b)
c 2  a 2  b2
Asintoti y  
b
b
x
a
c
V1 (a;0)
V2 (-a;0)
x
V4 (0;-b)
F2 (0;-c)
Matematica
www.mimmocorrado.it
1
Iperbole equilatera ( F1 , F2  Asse x )
L’equazione dell’iperbole equilatera con i fuochi sull’asse delle x è :
x 2  y 2  a2
y
yx
Asse trasverso = 2 a
Asse non trasverso = 2 a
Distanza focale = 2 c
V3 (0, a)
Eccentricità e  2
c 2  2 a2
Asintoti y   x

F2  a 2 ; 0


F1 a 2 ; 0

x
V1(a,0)
V2(-a,0)
V4 (0, -a)
y  x
Iperbole equilatera ( F1 , F2  Asse y )
L’equazione dell’iperbole equilatera con i fuochi sull’asse delle y è :
y 2  x 2  a2
y
yx
Asse trasverso = 2 a

F1 0 ; a 2
Asse non trasverso = 2 a

Distanza focale = 2 c
V3 (0, a)
Eccentricità e  2
c 2  2a2
V2(-a,0)
V1(a,0)
x
Asintoti y   x
V4 (0, -a)

F2 0 ;  a 2

y  x
Matematica
www.mimmocorrado.it
2
Iperbole equilatera riferita agli asintoti ( k > 0 )
y
L’equazione dell’iperbole equilatera
riferita agli asintoti è: x  y  k
con k 
k>0
a2
0
2

F1 2 k ; 2 k
L’iperbole si trova nel I° e III° quadrante.
V1

V2  k ;  k

F1  2 k ;  2 k

k; k


x


Iperbole equilatera riferita agli asintoti ( k < 0 )
y
k<0
L’equazione dell’iperbole equilatera
riferita agli asintoti è: x  y  k
con k 
a2
0
2
L’iperbole si trova nel II° e IV° quadrante.

F1   2 k ;  2 k


V2   k ;  k

x
V1
F1
Matematica
www.mimmocorrado.it


 k;   k
 2k ;   2k


3
Funzione omografica
La funzione omografica è un’iperbole equilatera con gli asintoti paralleli agli assi cartesiani.
L’equazione della funzione omografica è: y 
Gli asintoti hanno equazione: y 
a
c
e
ax  b
cx  d
con c  0
e ad  bc
cx  d  0
cx  d  0
y
 d a
C  ; 
 c c
y 
a
c
x
O
Considerazioni
Se c  0 l’equazione diventa y 
b
si ha: a  k  c e b  k  d .
d
ax  b
Sostituendo questi valori di a e di b nell’equazione y 
si ha:
cx  d
kcx  kd k  ( cx  d )
y

da cui si ha: y  k cx  d  0  .
cx  d
cx  d
 d

In definitiva per ad  bc si ottiene la retta orizzontale privata del punto P   ; k 
 c

Se ad  bc 
Matematica
a
b
c
d
a
b
(equazione di una retta)
x
d
d
e ponendo k 
www.mimmocorrado.it
4