ESERCIZI DI MATEMATICA
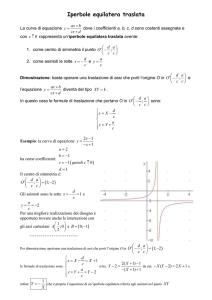
1. Le seguenti coppie di triangoli si corrispondono in una traslazione. Traccia gli assi (paralleli) di due simmetrie che, composte
fra loro, diano come risultato la traslazione:
2. Le seguenti coppie di triangoli si corrispondono in una rotazione. Traccia gli assi di due simmetrie che, composte fra loro,
diano come risultato la rotazione:
3. Abbiamo visto che è possibile scomporre una traslazione nel prodotto di due simmetrie assiali. Secondo te è possibile scomporre una simmetria assiale nel prodotto di due traslazioni? Perché?
4. Scrivi le equazioni della simmetria di centro C = (−1, 3) e applica la simmetria alla retta r di equazione y = 2x + 1. Detta r0 la
retta immagine:
(a) verifica che le due rette sono parallele;
(b) calcola la distanza fra le due rette (ricorda che in passato abbiamo ricavato una formula per trovare la distanza punto retta)
5. Sia data la parabola P di equazione y = x2 − 2x e sia P 0 la sua simmetrica rispetto al punto C = (2, 4).
(a) trova l’equazione di P 0 e traccia in un riferimento cartesiano ortogonale i grafici delle due parabole;
(b) calcola analiticamente le coordinate dei punti di intersezione fra le due parabole e verifica che si corrispondono nella
simmetria di centro C;
(c) verifica che anche le coordinate dei vertici e dei fuochi si corrispondono in tale simmetria;
(d) sia y = k l’equazione di una retta, essendo k un parametro; chiamiamo A e B le intersezioni della retta con la P (xA < xB );
per quali valori di k tali intersezioni esistono? (per quali valori di k è definito il discriminante dell’equazione che imposti
per trovare le intersezioni? quale signifiato geometrico dai alla limitazione su k?)
√
(e) trova, se esiste, un valore di k per cui il segmento AB abbia lunghezza 2 3.
Chi sa di aver bisogno di fare esercizi su equazioni e disequazioni di secondo grado, fattorizzazione e altre cose di algebra utilizzi
questi giorni per rimettersi in pari. Sul libro c’è tanto materiale per fare esercizio.