lezione 9

9. 5 novembre 2009
Geometria Analitica
Qualche esercizio sulla parabola
Cominciamo con qualche esercizio...
Esercizio Trovare l’equazione della parabola che ha vertice in V (1, 3) e passa per A(3, −1).
L’equazione generale della parabola è y = ax2 + bx + c. Per determinare in maniera univoca
la parabola, dobbiamo determinare i parametri a, b, c. Per farlo dobbiamo trovare 3 condizioni che
scriveremo in forma di equazioni.
b
∆
Poichè il vertice ha coordinate V (− , − ) e noi vogliamo che V = (1, 3), imponiamo ad esempio
2a 4a
∆
b
= 1 (si poteva anche imporre che −
= 3).
che −
2a
4a
Imponiamo poi che la parabola passi per V (1, 3), ovvero sostituiamo le coordinate di V nell’equazione generale ottenendo 3 = a + b + c.
Imponiamo infine che la parabola passi per A(3, −1), ovvero sostituiamo le coordinate di A nell’equazione generale ottenendo −1 = 9a + 3b + c.




b

 −
 b = −2a
 b = −2a
 b=2
=1
2a
⇒
a
−
2a
+
c
=
3
⇒
c
=
3
+
a
⇒
c=2
a+b+c=3





9a
−
6a
+
c
=
−1
a
=
−1
a = −1
9a + 3b + c = −1
Quindi l’equazione della parabola cercata è y = −x2 + 2x + 2
Esercizio Discutere la posizione reciproca della parabola y = x2 − 1 e della retta y = x − 1.
Per risolvere questo esercizio dobbiamo, in altre parole, trovare quante e quali soluzioni ha il
sistema
y = x2 − 1
y =x−1
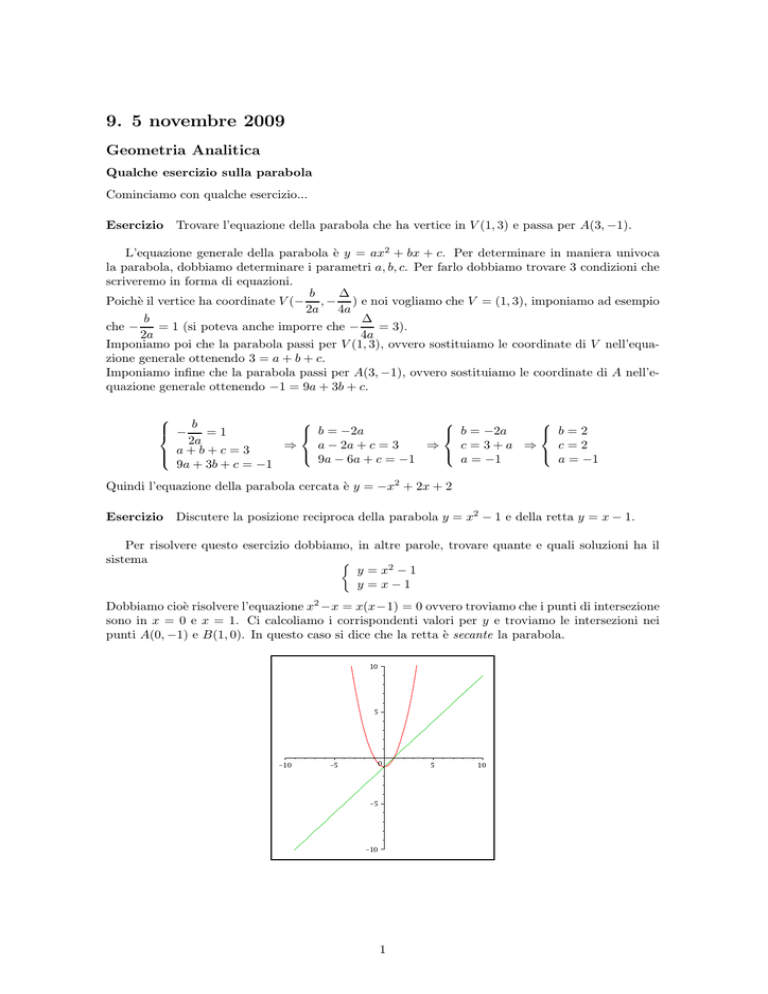
Dobbiamo cioè risolvere l’equazione x2 −x = x(x−1) = 0 ovvero troviamo che i punti di intersezione
sono in x = 0 e x = 1. Ci calcoliamo i corrispondenti valori per y e troviamo le intersezioni nei
punti A(0, −1) e B(1, 0). In questo caso si dice che la retta è secante la parabola.
10
5
K10
K5
0
K5
K10
1
5
10
L’iperbole equilatera
L’equazione generale dell’iperbole equilatera è
y=
k
k ∈ R, k 6= 0
x
L’iperbole è definita in R {0} e gli assi sono detti asintoti. Qui sotto tracciamo il grafico di y =
1
x
10
5
K
10
K
0
5
5
10
K
5
K
10
grafico di y=1/x
La funzione omografica
d a
ax + b
individua un’iperbole equilatera traslata nel punto (detto centro) C(− , ).
cx + d
c c
a
d
Gli assi y = e x = − son detti asintoti.
c
c
2x + 3
Come si pu vedere, il grafico di y =
è il grafico di un’iperbole equilatera traslata in
3x + 1
d a
1 2
C(− , ) = (− , )
c c
3 3
L’equazione y =
10
5
K10
K5
0
K5
K10
2
5
10