Precorso di Matematica
Argomenti proposti
Insiemi numerici
Numeri naturali
Numeri interi
Numeri razionali
Numeri reali
Calcolo letterale e polinomi
Divisione tra polinomi
Il teorema del resto
Equazioni di 2° grado e parabole, disequazioni di 2° grado
Parabola
Disequazioni di 2° grado
Equazioni e disequazioni irrazionali
Equazioni irrazionali
Disequazioni irrazionali
Sistemi: rette e sistemi lineari, sistemi di grado superiore al primo, sistemi di
disequazioni
Sistemi lineari
Appendice 1:
- Sistemi di grado superiore al primo, sistemi omogenei
Sistemi di disequazioni
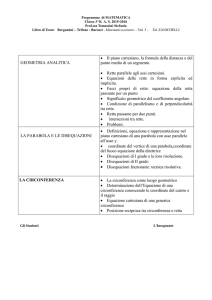
Le coniche: circonferenza, parabola, ellisse e iperbole
La circonferenza
La parabola
Ellisse e iperbole
Equazioni esponenziali e logaritmiche
Esponenziali
Equazioni esponenziali e logaritmi
Equazioni logaritmiche
Trigonometria
Relazioni fondamentali
Valori delle funzioni goniometriche di archi particolari
Variazione delle funzioni trigonometriche
Equazioni trigonometriche
Disequazioni trigonometriche
Formule di trigonometria
Appendice 1:
- Funzioni trigonometriche inverse
Appendice 2:
- Relazioni tra gli elementi di un triangolo
Formulario di Algebra
Insiemi numerici
NUMERI NATURALI
Una delle prime attività matematiche elementari è quella del “contare”.
I numeri che servono per contare: 1,2,3,4,….. sono detti numeri naturali (alcuni matematici
includono anche il numero 0 fra i naturali).
Fra i numeri naturali sono definite 2 operazioni fondamentali, sempre legate all’attività del
“contare”:
1) un’operazione, detta addizione, che ai generici numeri naturali x e y, associa il numero
naturale somma di x e y, che si indica col simbolo x+y (x,y sono gli addendi della somma)
2) un’operazione, detta moltiplicazione, che ai generici numeri naturali x e y, associa il numero
naturale prodotto di x e y, che si indica col simbolo xy o semplicemente con xy (x,y sono i
fattori del prodotto).
L’operazione di addizione gode delle seguenti proprietà:
1.1
a+b = b+a per ogni a, b numeri naturali (proprietà commutativa dell’addizione);
1.2 (a+b)+c = a+( b+c) per ogni a, b, c numeri naturali (proprietà associativa dell’addizione).
Analogamente l’operazione di moltiplicazione gode delle seguenti proprietà:
1.3
ab = ba per ogni a, b numeri naturali (proprietà commutativa della moltiplicazione);
1.4 (ab)c = a(bc) per ogni a, b, c numeri naturali (proprietà associativa della moltiplicazione).
1.5 se a,b,c sono numeri naturali e se ac=bc allora a=b (regola di cancellazione)
Vi è infine una proprietà che lega le 2 operazioni di addizione e moltiplicazione:
1.6 a(b+c) = ab+ac per ogni a,b,c numeri naturali (proprietà distributiva dell’addizione rispetto
al prodotto)
Rappresentazione dei numeri naturali su una retta orientata
Sia data una retta r orientata, in cui cioè abbiamo fissato un verso (convenzionalmente da sinistra
verso destra). Sulla retta r fissiamo poi un punto O (detto origine) ed un segmento OU la cui
lunghezza sarà la nostra unità di misura della lunghezza. Possiamo allora rappresentare ogni numero
naturale x come punto P sulla retta, riportando, nel verso fissato, a partire dall’origine O tante volte
il segmento OU quante sono le unità contenute in x:
O
U
1 2
3
P
4 5
Il numero naturale x associato al punto P sulla retta è detto ascissa del punto, e rappresenta la
misura del segmento OP rispetto all’unità di misura fissata. Nella figura precedente l’ascissa del
punto P è 4, l’ascissa del punto U è 1.
Ordinamento dei numeri naturali
Fra i numeri naturali si può stabilire un ordinamento. Dati due numeri naturali a,b si dice che a è
maggiore di b (o equivalentemente che b minore di a) , e si scrive a>b (equivalentemente b<a), se
esiste un numero naturale c che sommato al numero b dia come risultato a, cioè che soddisfi
l’eguaglianza b+c=a. Nella rappresentazione geometrica sulla retta orientata ciò equivale ad
affermare che il punto corrispondente al numero a precede il punto corrispondente al numero b, nel
verso stabilito sulla retta (quindi procedendo da sinistra verso destra).
Le proprietà fondamentali dell’ordinamento dei numeri naturali sono
1.7 Se a,b sono numeri naturali e se a<b e b<c allora a<c (proprietà transitiva)
1.8 Se a,b sono numeri naturali e se a<b allora per ogni numero naturale c si ha anche a+c<b+c e
ac<bc.
1.9 Se a,b,c,d sono numeri naturali e se a<b e c<d allora ac<bd
Dati due numeri naturali a,b si dice che a è maggiore o uguale a b, e si scrive ab, se a>b oppure
a=b.
Potenza
L’elevamento a potenza xy di un numero naturale x elevato al numero naturale y si definisce come
prodotto di un numero y di fattori tutti uguali ad x (almeno nel caso in cui y sia diverso da 1). Il
numero x si dice base della potenza, e il numero y si dice esponente.
Per esempio:
25 = 2 · 2 · 2 · 2 · 2.
In generale
xy = xxx…x
(dove y è il numero dei fattori).
Nel caso in cui l’esponente y sia uguale a 1, convenzionalmente si definisce x1=x .
Valgono le seguenti proprietà delle potenze (dove x,y,z indicano generici numeri naturali)
1.10
xyxz = xy+z ;
1.11 (xy)z = xzyz;
1.12 (xy)z = xyz;
Divisori e multipli
Dati due numeri naturali a,b si dice che a è un divisore di b, o equivalentemente che b è un multiplo
di a, se esiste un numero naturale c che moltiplicato per a dia come risultato b, cioè che soddisfi
l’eguaglianza ac=b.
Ogni numero naturale a è multiplo di 1 e di a stesso.
Un numero naturale p diverso da 1 si dice primo se ammette come divisori solo 1 e p.
Esempi di numeri primi sono 2,3,5,7,11.
Se un numero non è primo, e quindi ammette almeno un divisore diverso da 1 e da sé stesso, si dice
composto.
Fra i numeri naturali, i numeri primi sono particolarmente importanti perché ogni numero naturale
non primo diverso da 1 può essere espresso come prodotto di numeri primi; questa scrittura prende
il nome di fattorizzazione in fattori primi, e questa fattorizzazione è unica (Teorema fondamentale
dell’aritmetica).
Convenzionalmente si può considerare la fattorizzazione anche di un numero primo p, in cui vi è un
solo fattore primo, coincidente con p stesso.
Esempi di fattorizzazioni in primi sono:
12=223
700=22557
11=11
Se fattorizziamo un numero naturale in prodotto di numeri primi, raccogliendo i fattori uguali si può
fattorizzare il numero come prodotto di potenze di numeri primi, con basi tutte diverse.
Per esempio:
12=2231
700=22527
11=111
Il Massimo Comun Divisore di due numeri naturali a,b (indicato con il simbolo MCD(a,b) ) è il
maggiore dei divisori comuni di a,b e si ottiene (se a,b sono diversi da 1) scomponendo i numeri in
prodotto di potenze di fattori primi e moltiplicando tra di loro solo i fattori comuni elevati al
minimo esponente.
Per esempio:
12=2231, 90=213251 MCD(12,90)=2131=6
Quando MCD(a,b) si dice che a e b sono primi fra loro (il che equivale ad affermare che non hanno
fattori primi in comune).
Il minimo comune multiplo di due numeri naturali a,b (indicato con il simbolo mcm(a,b) è il minore
dei multipli comuni di a,b e si ottiene (se a,b sono diversi da 1) scomponendo i numeri in prodotto
di potenze di fattori primi e moltiplicando tra di loro i fattori comuni e non comuni elevati al
massimo esponente.
Per esempio:
12=2231, 90=213251 mcm(12,90)=223251=180
Divisione fra numeri naturali
Siano dati due numeri naturali a,b, con ba.
Se a è divisore di b, il numero naturale c tale che ac=b è detto anche risultato della divisione di b
per a o quoziente.
Anche nel caso in cui a non sia divisore di b, si può effettuare una divisione con resto di b per a,
cioè trovare due numeri naturali q,r ,detti quoziente e resto, tali che b=aq+r, dove il resto r è <a.
NUMERI INTERI RELATIVI
Se a,b sono numeri naturali, con a>b, si può trovare un numero naturale c tale che a=b+c. Tale
numero naturale c è detto risultato della sottrazione di b da a.
Per permettere la sottrazione anche nel caso in cui sia ab si costruiscono i cosiddetti numeri interi
relativi (o semplicemente numeri interi): 0,+1,-1,+2,-2,+3,-3,…..
Un numero intero relativo è 0 oppure è una coppia formata da un segno, + o -, e da un numero
naturale.
Un numero intero relativo diverso da 0 è detto positivo se il suo segno è +, negativo se il suo segno
è-.
I numeri naturali si identificano con i numeri interi relativi con segno + . Quindi 1=+1, 2=+2 etc.
Si dice valore assoluto di un numero intero relativo il numero naturale ottenuto non considerando il
segno (se il numero è diverso da 0); il valore assoluto di 0 è 0.
Anche fra i numeri interi relativi si possono definire le operazioni di somma e di prodotto, che
estendono quelle dei numeri naturali.
Definiamo la somma di due numeri interi relativi.
Se almeno uno dei due numeri interi relativi a,b coincide con 0, la somma a+b è uguale all’altro
addendo (il numero 0 è neutro rispetto alla somma).
La somma a+b di due numeri interi relativi a,b (diversi da 0) di ugual segno è un numero dello
stesso segno; il suo valore assoluto è la somma dei valori assoluti di a e b. La somma di due numeri
interi relativi a,b (diversi da 0) di segno diverso e con valori assoluti diversi è un numero che ha il
segno dell’addendo di valore assoluto maggiore; il suo valore assoluto è la differenza dei valori
assoluti di c e d. La somma di due numeri interi relativi a e b di segno diverso e con valori assoluti
uguali è 0.
Esempio:
(+2)+(+3) = +5; (-2)+(–7) = -9; (-5)+(+10) = +5; (+6)+(-6)=0; (+4)+0=4
Definiamo il prodotto di due numeri interi relativi.
Se almeno uno dei due numeri interi relativi a,b coincide con 0, il prodotto ab è uguale a 0.
Il prodotto ab di due numeri interi relativi a,b (diversi da 0) è il numero che ha come valore
assoluto il prodotto dei valori assoluti, ed il segno + se a,b hanno stesso segno, il segno – se se a,b
hanno segno diverso (regola del segno del prodotto)
Esempio:
(+2)0=0; (+3)(+5)=+15; (-2)(+6)=-12; (-4)(-5)=+20.
Per la somma e il prodotto di numeri interi relativi valgono le stesse proprietà da 1.1 a 1.6 delle
analoghe operazioni dei numeri naturali; la regola di cancellazione 1.5 si deve però modificare
come segue:
se a,b,c sono numeri interi relativi con c0 e se ac=bc allora a=b (regola di cancellazione)
Inoltre valgono le proprietà:
1.13 Il numero 0 è neutro rispetto alla somma (come si è visto nella definizione di somma di numeri
interi relativi)
1.14 Per ogni intero relativo a esiste un intero relativo (detto opposto di a) che sommato ad a dà
come risultato il numero 0: l’opposto del numero 0 è 0, l’opposto di un numero intero relativo
diverso da 0 ha lo stesso valore assoluto e segno diverso. L’opposto dell’intero relativo a si indica
con il simbolo –a. Quindi: -0=0, -(+5)=-5, -(-6)=+6.
Come già detto, fra i numeri interi relativi è sempre possibile effettuare la sottrazione: comunque
dati due interi relativi a,b esiste sempre un intero relativo c che sommato ad a dà come risultato b, e
tale intero relativo c è detto risultato della sottrazione di a da b,ed è indicato con il simbolo b-a.
Tale numero c si determina semplicemente sommando b con l’opposto di a: c=b-a=b+(-a).
Rappresentazione dei numeri interi relativi su una retta orientata
Sia data una retta r orientata, in cui cioè abbiamo fissato un verso (convenzionalmente da sinistra
verso destra). Sulla retta r fissiamo poi un punto O (detto origine) ed un segmento OU la cui
lunghezza sarà la nostra unità di misura della lunghezza. Possiamo allora rappresentare ogni numero
naturale x come punto P sulla retta nel modo seguente: se x=0 associamo ad x il punto origine O; se
x è positivo, associamo ad x il punto ottenuto riportando, nel verso fissato, a partire dall’origine O
tante volte il segmento OU quante sono le unità contenute nel valore assoluto di x; se x è negativo,
associamo ad x il punto ottenuto riportando, nel verso opposto a quello fissato, a partire dall’origine
O tante volte il segmento OU quante sono le unità contenute nel valore assoluto di x:
Q
O U
-3 -2 -1 0 1
2
P
3 4
5
Il numero naturale x associato al punto P sulla retta è detto ascissa del punto. Nella figura
precedente l’ascissa del punto P è 4, l’ascissa del punto Q è -2.
Ordinamento dei numeri interi relativi
Fra i numeri interi relativi si può stabilire un ordinamento, che estende quello dei numeri naturali.
Dati due numeri interi relativi a,b si dice che a è maggiore di b (o equivalentemente che b minore di
a) , e si scrive a>b (equivalentemente b<a), se esiste un numero naturale c che sommato al numero
b dia come risultato a, cioè che soddisfi l’eguaglianza b+c=a. Nella rappresentazione geometrica
sulla retta orientata ciò equivale ad affermare che il punto corrispondente al numero a precede il
punto corrispondente al numero b, nel verso stabilito sulla retta (quindi procedendo da sinistra verso
destra). I numeri interi relativi positivi coincideranno con i numeri >0, quelli negativi con i numeri
<0.
Le proprietà fondamentali dell’ordinamento dei numeri interi relativi sono:
1.15 Se a,b sono numeri interi relativi e se a<b e b<c allora a<c (proprietà transitiva)
1.16 Se a,b sono numeri interi relativi e se a<b allora per ogni numero intero relativo c si ha anche
a+c<b+c
1.17 Se a,b sono numeri interi relativi e se a<b allora per ogni numero intero relativo positivo c si
ha anche ac<bc
Dati due numeri interi relativi a,b si dice che a è maggiore o uguale a b, e si scrive ab, se a>b
oppure a=b.
NUMERI RAZIONALI
Abbiamo visto che, dati due numeri naturali a,b, non sempre é possibile eseguire la divisione di a
per b, cioè trovare un numero naturale c tale che a=bc. Per ovviare a ciò si costruiscono i numeri
razionali.
Un numero razionale è una frazione della forma a/b con a, b numeri naturali, e con b0; a è detto
numeratore, b denominatore. Due frazioni distinte possono rappresentare lo stesso numero
razionale, secondo la regola seguente: a/b = c/d quando ad=bc (regola del “prodotto in croce”).
Esempio:
3/5 = 12/20
Dato un numero razionale a/b, se a,b sono multipli dello stesso numero naturale c, dividendo
numeratore e denominatore entrambi per c si ottiene una frazione che rappresenta lo stesso numero
razionale: ciò si vede facilmente scrivendo a=cd, b=ce (dove d,e sono numeri naturali) e
osservando che a/b=d/e per la regola del prodotto in croce (in quanto si ricava ae=cde=bd).
Se a e b sono primi fra loro la frazione a/b si dice ridotta ai minimi termini. Una qualunque frazione
si può sempre ridurre ai minimi termini, dividendo numeratore e denominatore per il loro MCD.
I numeri razionali con denominatore 1 si identificano con il numero naturale al numeratore. Quindi:
3/1=3, 7/1=7.
Anche fra i numeri razionali si definiscono le operazioni di somma e prodotto, secondo le seguenti
regole:
a c ad bc
b d
bd
a c ac
b d bd
Rispetto a tali operazioni valgono le proprietà già viste per i numeri naturali, ma con l’ulteriore
proprietà:
1.18 Comunque dato un numero razionale x=a/b, esiste un numero razionale (detto inverso o
reciproco di x e indicato col simbolo x-1) che moltiplicato per x dà come risultato 1. Per ottenere x-1
basta considerare il razionale b/a: infatti (a/b)(b/a)=(ab)/(ba)=1/1=1.
Dati due razionali qualunque x=a/b, y=c/d, si può sempre effettuare la divisione di x per y, cioè
trovare un razionale z tale che x=yz; basta infatti scegliere il razionale z= xy-1=(a/b)(d/c)=(ad)/(bc).
Il risultato di tale divisione di x per y è indicato anche con x/y.
Ogni numero razionale x=a/b si può rappresentare come numero decimale, con una parte intera
(numero naturale oppure 0) e una successione di cifre dopo la virgola.
Per ottenere tale rappresentazione basta effettuare il noto procedimento di “divisione con la virgola”
del numeratore per il denominatore: si otterrà sempre un numero che da un certo posto in poi ha
tutte cifre uguali a 0, oppure un numero periodico, in cui un gruppo di cifre (che formano un
numero naturale detto periodo) si ripete indefinitivamente da un certo posto in poi.
Esempi:
3/5=0,60000….=0,6
13/3=4,333333…. = 4, 3 (periodo=3)
131/55=2,381818181…= 2,381 (periodo=81)
Il numero naturale formato dalle (eventuali) cifre dopo la virgola che precedono le cifre del periodo
è detto antiperiodo.
Ricordiamo che il procedimento inverso per trasformare un numero periodico in frazione è il
seguente: si costruisce una frazione in cui il numeratore è la differenza fra il numero che si ottiene
togliendo la virgola e il numero ottenuto con le cifre che precedono il periodo, e in cui il
denominatore è un numero formato da tante cifre 9 quante sono le cifre del periodo e da tante cifre
0 quante sono le (eventuali) cifre dell’antiperiodo.
Negli esempi precedenti:
4, 3 =(43-4)/9=39/9=13/3
2,381 =(2381-23)/990=2358/990=131/55
Rappresentazione dei numeri razionali su una retta orientata
Sia data una retta r orientata, in cui cioè abbiamo fissato un verso (convenzionalmente da sinistra
verso destra). Sulla retta r fissiamo poi un punto O (detto origine) ed un segmento OU la cui
lunghezza sarà la nostra unità di misura della lunghezza. Possiamo allora rappresentare ogni numero
razionale x=a/b come punto P sulla retta nel modo seguente: consideriamo il sottomultiplo di OU
ottenuto suddividendo OU in b parti uguali, e riportiamo, nel verso fissato, a partire dall’origine O
tante volte tale sottomultiplo quante sono le unità contenute nel numero a:
O
U
P
Il numero razionale x associato al punto P sulla retta è detto ascissa del punto. Nella figura
precedente l’ascissa del punto P è 5/3.
Ordinamento dei numeri razionali
Fra i numeri razionali si può stabilire un ordinamento, che estende quello dei numeri naturali. Dati
due numeri razionali x,y si dice che x è maggiore di y (o equivalentemente che y minore di x) , e si
scrive x>y (equivalentemente y<x), se esiste un numero razionale z che sommato al numero y dia
come risultato x, cioè che soddisfi l’eguaglianza y+z=x. Nella rappresentazione geometrica sulla
retta orientata ciò equivale ad affermare che il punto corrispondente al numero x precede il punto
corrispondente al numero z.
Questo ordinamento dei numeri razionali soddisfa le proprietà analoghe alle 1.7, 1.8, 1.9
dell’ordinamento dei numeri naturali.
NUMERI RAZIONALI RELATIVI
In modo analogo a quanto fatto per costruire, a partire dai numeri naturali, i numeri interi relativi, si
possono costruire i numeri razionali relativi a partire dai numeri razionali. Basta considerare, oltre
che il numero 0 (identificato con una qualunque frazione con numeratore 0 e denominatore diverso
da 0), tutte le frazioni a/b con segno + o -.
E’ facile generalizzare tutte le costruzioni relative alle operazioni di somma, prodotto,
rappresentazione su una retta orientata, ordinamento.
Nell’insieme dei numeri razionali relativi, ogni numero x diverso da 0 ha un inverso x-1 tale che il
prodotto xx-1=1.
NUMERI REALI
Le rappresentazioni di tutti i possibili numeri razionali relativi come punti di una retta orientata non
“esauriscono” tutti i punti della retta.
Per esempio, se OU è l’unità di misura della lunghezza, consideriamo un quadrato di lato OU,
quindi di lunghezza uguale ad 1. Se riportiamo a partire da O sulla retta orientata nel verso positivo
fissato un segmento OP di lunghezza uguale a quella della diagonale, l’ascissa di P rappresenta, per
il teorema di Pitagora un numero x che al quadrato coincide con 12+12=2 (x è la cosiddetta “radice
quadrata di 2”).
Ora tale numero x non è un numero razionale, cioè non è possibile esprimere x sotto forma di
frazione x=a/b dove a,b sono numeri naturali (una dimostrazione esauriente di questa affermazione
sarà fornita durante il corso di Matematica Discreta I).
Considerando i “numeri” associati a tutti i punti della retta orientata si ottengono appunto i
cosiddetti numeri reali, la cui trattazione formale esula dagli scopi di questo precorso, e viene
rimandata al corso di Analisi I. Possiamo solo accennare al fatto che i numeri reali hanno una
rappresentazione sotto forma di numero decimale, con una parte intera e una successione di cifre
dopo la virgola. Fra di essi i numeri razionali si distinguono, come già visto, perché da un certo
posto in poi hanno tutte cifre uguali a 0, oppure sono numeri periodici, in cui un gruppo di cifre
(periodo) si ripete indefinitivamente da un certo posto in poi. I numeri reali non razionali (detti
numeri irrazionali) hanno invece una successione infinita di cifre dopo la virgola senza questa
“regolarità”.
Esempio:
La radice quadrata di 2 in forma decimale é uguale a 1,41421356237309…………
Calcolo letterale e Polinomi
CALCOLO LETTERALE
Perché il calcolo letterale?
La matematica ha a che fare con il ''calcolare''. Ma in ogni libro di matematica i calcoli vengono
eseguiti su lettere invece che su numeri.
Il vantaggio di questo modo di procedere è quello di ottenere dei risultati generali che valgono
qualunque sia il valore numerico attribuito alle lettere.
Per esempio la proprietà distributiva della somma rispetto al prodotto (che vale in generale per tutti
i numeri reali) si esprime con una eguaglianza fra espressioni letterali:
a(b+c)=ac+bc
ed esprime appunto una regola “generale” che resta valida qualunque sia il valore numerico reale
attribuito alle lettere a,b,c.
Otteniamo le espressioni algebriche fissando delle lettere (variabili) e manipolandole con l’utilizzo
dei numeri e delle operazioni di somma e prodotto (l’operazione di sottrazione è in fondo una
somma con l’opposto).
Esempi di espressioni algebriche sono: (2a+b-3c2), (4x-3y)3 ed altre più complicate.
Se interviene anche l’operazione di divisione, otteniamo le espressioni algebriche fratte.
Esempio: (2a+b-3c2)/(4x-3y)3
Naturalmente, in questo caso, non è detto che l’espressione abbia un valore compiuto per ogni
valore numerico assegnato alle variabili: per esempio valori che rendono il denominatore uguale a 0
non permettono di calcolare il valore numerico dell’espressione.
Abbiamo già visto che le espressioni possono essere utilizzate per scrivere regole di calcolo. La
struttura di fondo è sempre la stessa: si scrivono due espressioni di aspetto diverso che però hanno
la proprietà di produrre sempre lo stesso risultato quando sostituiamo le variabili con numeri
concreti. Tali enunciati si chiamano identità. Un esempio di identità è appunto, come visto,
l’eguaglianza che esprime la proprietà distributiva della somma rispetto al prodotto:
a(b+c)=ab+ac
Il procedimento che permette di passare dall’espressione ab+ac all’espressione “identica” a(b+c) è
spesso descritto con la frase “mettere in evidenza la variabile a”.
Si possono naturalmente ottenere identità più complicate. Per esempio proviamo a “sviluppare”
l’espressione (a+b)(x+y). Utilizzando una prima volta la proprietà distributiva otteniamo l’identità:
(a+b)(x+y)= (a+b)x+(a+b)y
Utilizzando di nuovo la proprietà distributiva otteniamo l’identità:
(a+b)(x+y)=ax+bx+ay+by
Alcune identità notevoli sono spesso molto utili per lo sviluppo delle espressioni algebriche.
Ne elenchiamo alcune:
a2-b2 =(a+b)(a-b)
(differenza di quadrati)
3 3
2
2
a -b =(a-b)(a +ab+b )
(differenza di cubi)
a3+b3 =(a+b)(a2-ab+b2)
(somma di cubi)
2
2
2
(a+b) =a +2ab+b
(quadrato di un binomio)
(a+b)3=a3+3ab2+3a2b+b3
(cubo di un binomio)
POLINOMI
Un’espressione algebrica nella variabile x, in cui si utilizzano numeri reali (detti coefficienti) e le
operazioni di somma e prodotto è detta polinomio in x, e indicata genericamente con un simbolo del
tipo P(x) o simili.
La forma generale di un polinomio in x è la somma di monomi in x, ognuno ottenuto moltiplicando
un coefficiente numerico per una potenza della variabile x (per convenzione si pone x0=1). Il grado
del monomio è l’esponente della potenza di x che in esso compare.
Per esempio il polinomio P(x)=3+2x+0x2+5x3 e la somma dei 4 monomi 3, 2x, 0x2, 5x3 di grado
rispettivamente 0,1,2,3. I monomi con coefficiente 0 in genere si omettono, quindi il precedente
polinomio si scrive anche P(x)=3+2x+5x3. Il grado del polinomio P(x) (che non sia il polinomio
“nullo” cioè con tutti i coefficienti uguali a 0) è il massimo dei gradi dei monomi (con coefficiente
non nullo) di cui è somma. Il polinomio precedente P(x) ha grado 3.
Un polinomio di grado 0 coincide con un valore numerico: P(x)=a (dove a è un numero reale).
Dato un polinomio P(x) ed un numero reale a, si chiama valore assunto da P(x) in a quel numero
reale che si calcola sostituendo la variabile x con a. Tale valore si indica con P(a).
Esempio: se P(x)=3x2+2x+5, si ha P(1)=10, P(-2)=13, P(0)=5.
Come tutte le espressioni algebriche, i polinomi in x si possono sommare e moltiplicare.
Dati due polinomi non nulli P(x) e S(x), effettuare la divisione di P(x) per S(x) significa trovare due
polinomi Q(x), R(x) (detti rispettivamente quoziente e resto della divisione) tali che
P(x)=S(x)Q(x)+R(x)
dove il resto R(x) può essere nullo (in caso di divisione “esatta”) oppure essere non nullo ma di
grado inferiore al grado di S(x).
L’algoritmo per calcolare quoziente e resto della divisione fra P(x) e S(x) è ben noto:
a. Se il polinomio P(x) ha grado minore del grado di S(x), la divisione è immediata, ponendo
quoziente Q(x)=0 e resto R(x)=P(x). Negli altri casi:
b. si ordinano i due polinomi secondo le potenze decrescenti di x. Se il polinomio P(x) è
incompleto, si introducono i termini mancanti con coefficiente nullo.
c. Si divide il primo monomio di P(x) per il primo monomio di S(x) (dove “dividere” un monomio
per un altro dà come risultato un monomio in cui il coefficiente è la divisione dei coefficienti, e
l’esponente della x è la differenza degli esponenti); il quoziente ottenuto è il primo monomio del
polinomio quoziente Q(x).
d. Si moltiplica questo primo monomio per S(x) e si sottrae il risultato da P(x). Si ottiene il primo
resto parziale.
e. Si procede di nuovo come punto c., sostituendo P(x) con il resto parziale. Si ripete l’algoritmo
finché si ottiene un resto parziale nullo o di grado inferiore a quello del divisore: quest’ultimo resto
parziale è il resto R(x) della divisione, mentre il quoziente Q(x) è la somma dei monomi quoziente
ottenuti nel punto c.
Esempio: dividiamo il polinomio P(x)=x4-2x3+4x-3 per il polinomio S(x)=x2+2x-2.
x4 -2x3 + 0x2 + 4x - 3
x2+2x-2
4
3
2
x +2x -2x
-------------------------------------x2-4x+10
3
2
-4x +2x +4x -3
-4x3 -8x2 +8x
--------------------------10x2 -4x -3
10x2+20x-20
---------------------------24x+17
Si ottiene quoziente Q(x)= x2-4x+10 e resto R(x)= -24x+17
Se dividiamo un polinomio P(x) non nullo per un polinomio S(x) di grado 1, il resto R(x) sarà o
nullo o non nullo di grado 0 (quindi un numero in ogni caso).
Citiamo il:
Teorema del resto: Se P(x) è un polinomio non nullo, e se S(x) è un polinomio di grado 1 della
forma S(x)=x-a (dove a è un numero reale fissato), nella divisione di P(x) per S(x) il resto R(x) (che
è un numero per quanto detto prima) coincide con il valore P(a) assunto dal polinomio P(x) in a.
Per esempio se dividiamo il polinomio P(x)=3x3+2x2-x+7 per il polinomio S(x)=x-2, il resto R(x)
sarà il valore assunto da P(x) per x=2, cioè il valore P(2)=323+222-2+7=37.
Se il valore P(a) assunto dal polinomio P(x) in a è 0, si dice che il numero reale a è una soluzione
dell’equazione P(x)=0.
Per esempio, se P(x)=x2-3x+2, il numero a=1 è soluzione dell’equazione x2-3x+2=0 in quanto
P(1)=0, mentre a=0 non è soluzione della stessa equazione perché P(0)=20.
Il Teorema del resto afferma allora che se il numero reale a è soluzione dell’equazione P(x)=0, il
polinomio P(x) diviso per il polinomio (x-a) dà resto 0, cioè P(x) è esattamente divisibile per (x-a),
e si può scomporre in P(x)=(x-a)Q(x) (dove Q(x) è il quoziente della divisione). Questo permette di
“fattorizzare” un polinomio, conoscendo qualcuna delle soluzioni dell’equazione corrispondente.
Esercizi
1. Eseguire le seguenti divisioni:
( x 4 3x 2 4) : ( x 2 4)
[ Q(x)=x2+7 ; R(x)=24 ]
(7x - x3 + 2 + x2) : (x2 – 2)
[ Q(x)=-x+1 ; R(x)=5x+4]
2. Calcolare il resto senza eseguire la divisione:
( x 4 3x 2 5) : ( x 2)
[ R(x)=-9 ]
3. Dato P(x)=x3+x2-2x, calcolare i valori P(1) e P(-2) e fattorizzare opportunamente P(x).
[ P(x)=x(x-1)(x+2) ]
4. Semplificare le seguenti espressioni:
x 22 3x 2x 2 x 23 x 2 x 8
16x 8
x 13 3x 12 3x 1 1
[ x 2 ]
3
Equazioni di 2º grado e parabole, disequazioni di
2º grado
Teoria in sintesi
PARABOLA
2
Ogni funzione y ax bx c , con a 0, rappresenta una parabola, con le seguenti caratteristiche:
L'asse della parabola è parallelo all'asse delle y
b
xV
2a (l'ordinata si può trovare sostituendo questo valore nella
Il vertice ha ascissa
funzione)
La parabola ha la concavità rivolta verso l'alto se a 0 , verso il basso se a 0
La "apertura" della parabola è tanto minore quanto maggiore èa.
b
V
;...
Per tracciare il grafico qualitativo della parabola si determinano il vertice 2a e le
intersezioni con gli assi.
N.B.: Per queste ultime ricorda che devi risolvere i due sistemi
x 0
x 0
2
y ax bx c
y c
che dà
y 0
2
ax bx c 0
che dà
y 0
b b 2 4ac
x
1, 2
2a
DISEQUAZIONI DI 2º GRADO
ax 2 bx c 0
ax 2 bx c 0
N.B.: Possiamo sempre fare riferimento ai casi in cui il coefficiente a è positivo. Infatti se a è
negativo, basta cambiare segno a tutti i termini e invertire il senso delle disequazioni.
2
2
(esempio: x 2 x 3 0 è equivalente a x 2 x 3 0 )
METODO GRAFICO (uso della parabola)
Per dare una interpretazione grafica delle disequazioni di secondo grado
ax 2 bx c 0
ax 2 bx c 0
a) a) si disegna la parabola;
b) b) si cercano gli eventuali punti di intersezione della parabola con l'asse x;
c) c) si considerano le soluzioni delle disequazioni che sono date dalle ascisse dei punti della
2
parabola che hanno ordinata positiva ( y 0 ax bx c 0) oppure negativa
( y 0 ax 2 bx c 0) .
I casi possibili risultano riassunti nel seguente schema:
ax 2 bx c 0
ax 2 bx c 0
Costruisci tu per questo caso lo schema riassuntivo in modo analogo. Ricorda che in questo caso si
procede considerando la parte di parabola che sta nel semipiano delle y negative.
DECOMPOSIZIONE DEL TRINOMIO DI SECONDO GRADO
La risoluzione analitica delle disequazioni
ax 2 bx c 0
(ax 2 bx c 0)
avviene nel modo seguente
2
1. ax bx c 0
0
2
dette x1 ; x2 le due soluzioni di ax bx c 0 e posto x1 x2 si ha
ax 2 bx c a( x x1 )( x x2 )
E quindi, dalle regole dei segni, otteniamo la soluzione
x x1 x x2
(N.B.: Il simbolo , preso in prestito dalla logica, sta a significare che si considera l’unione
dei due insiemi x x1 , x x2 ).
ax 2 bx c a( x x1 ) 2
2. 0
quindi soluzione
x x1
3. 0
soluzione
R
2
Invece per la disequazione ax bx c 0 in modo analogo si ottiene:
1. 0
x1 x x2 , ossia per valori interni all'intervallo di estremi x1 , x2 ;
2. 0
non è mai verificata;
3. 0
non è mai verificata;
Svolgere per esercizio uno schema analogo al caso precedente.
Esercizi
1. 1. Tracciare il grafico qualitativo delle seguenti parabole, dopo averne trovato il vertice e
l'intersezione con gli assi:
a) a)
y x2 ,
y x 2 ,
b) b)
y 2 x 2 x 1;
c) c)
y x 2 4 x 10 ;
d) d)
y x 2 2x 1 ;
e) e)
y x 2 3x 2 ;
y x 2 1,
y ( x 2 1) ,
y x 2 1,
y ( x 2 1) ;
2. 2. Risolvere in , dopo aver impostato la discussione, le seguenti equazioni:
x
x
2x 3
2
; x 2 6 x 20 0
x 1 x 2 x 3x 2
(Non ha soluzioni)
x 1 x 2 2( x 2 4)
x2 x2
x2 4
(Non ha soluzioni)
x2 x
4x 2 1
1;
20
x 1
2x 1
(Si possono semplificare i conti?)
1 1
6
4
x 2 x 1 x
[5 , 2]
1
4
1
1 x
1 x 3 x 1 x 1
1
2 , 2
7 x 10
5
x5
x 6x 8 2 x x 4
[5]
( x 1) 2 1
4x
0
2
4x 4x 1 2x 1
0 ,
2
2
9
3. 3. Risolvere le seguenti disequazioni di secondo grado utilizzando il metodo grafico
(parabola…)
2
2
x2 1 0
a) a) x 0 x 0
x 2 0 x 2 0 ( x 2 1) 0
2
2
2
b) b) 3x x 2 0 ; 25 x 2 x 4 0 ; 12 x 3x 1 0
2
2
x
3 x 1;
5
nessuna soluzione
4. 4. Risolvere usando il metodo di decomposizione del trinomio di secondo grado.
2
a) a) x 3x 2 0
[ x 2 x 1];
b) b)
x 2 x 12 0
[3 x 4]
x 3 3x 2 4 x 12 0
3
2
[Ricorda: x 3x 4 x 12 ( x 2) (....), ]
N.B.: questo è uno dei rari casi fortunati in cui troviamo ad occhio una soluzione
dell’equazione corrispondente di terzo grado. In generale questo non è possibile. Vedremo
comunque nel corso che disequazioni come queste si risolvono facilmente con metodi
grafici.
x 4 13x 2 36 0
c) c)
2
[Poni: x y ;
y 2 13 y 36 0.... ,
y 19 y 19 ]
x3 8 0
d) d)
3
3
2
2
[Ricorda: a b (a b)(a ab b ) , x 2 ]
5. 5. Equazioni frazionarie:
N.B.: Ricorda sempre di imporre che i denominatori siano diversi da zero.
1
9
29
1
3
2
2
x 3 x 8 x 2 x 2 x 24 x x 4 x
m.c.m 8 x( x 3)( x 4)
2
7
x 9
x2
3x
1 2x
2
2
x 2 x 3 ( x 2)( x 2 x 3) x 5 x 6
2
6. 6.
x 5
N.B.: m.c.m ( x 1)( x 3)( x 2)
x2 1
x2 x2
: 1
x 0
x 2 2
x 2 x 2
[impossibile]
2
N.B.: L'equazione risolutiva, dopo aver svolto i passaggi è: 3 x 5 x 6 0
7. 7. Equazioni letterali
0,
5a
3 in questa equazione a può essere qualunque?]
3 x 5ax 0
[
9x a 0
[Qual'è l'unico caso per cui questa equazione è possibile?]
2
2
2
2ax b 0
xa xa
0
xa xa
2
[
b
2a , se a, b > 0: discutere attentamente gli altri casi]
[impossibile, attenzione a considerare i vari casi]
ab
a b
x 2 x
0
6
2 3
a b
2 , 3
xa xb
( a b) 2
x b x a ( x a)( x b)
[impossibile]
a2
x
a
2
x ax x a x
[a]
8. 8. Risolvere le seguenti equazioni nelle quali compaiono dei valori assoluti:
x 2 5x 6
[6 , 1, 3, 2]
x 2 3x 1 1
[0 , 3, 2 , 1]
6 x2 6
[0 , 0 , 12 ]
x2 2
1
x
[2 , 1, 1, 2]
Esempio di procedure possibili
2
x 5x 0
2
1. x 5 x 0
x 2 5x 6
5x x 2 6
2. Risolvere graficamente, trovando l'intersezione tra la retta y=6 e la curva di equazione
y x 2 5x
.
Le equazioni e disequazioni irrazionali
Teoria in sintesi
EQUAZIONI IRRAZIONALI
Un'equazione è irrazionale se contiene almeno un radicale nel cui radicando compare l'incognita.
Ad esempio
2 x 4 3x , è un'equazione irrazionale;
4x 2 6 , non è un'equazione irrazionale.
Data un'equazione A(x)=B(x), consideriamo l'equazione A x B x :
se n è pari, essa ha come soluzioni, oltre a quelle di A(x)=B(x), anche quelle di A(x)=B(x);
se n è dispari, essa è equivalente a quella data.
n
n
N.B.: Prova a risolvere la seguente equazione
2x 1 x 9
e l'equazione
(2 x 1) 2 ( x 9) 2
Si ottengono le stesse soluzioni? Le due equazioni sono equivalenti?
x1 10
8
x 2 3
[La prima equazione dà come soluzione x 10 , la seconda invece
]
Per risolvere un'equazione irrazionale
n
A( x) B( x)
è necessario "liberarci" in qualche modo dei radicali presenti, per ricondurre il problema alla
soluzione di una equazione razionale che ci dia buone informazioni sulle soluzioni dell'equazione
iniziale. Per fare questo operativamente dobbiamo:
elevare a n entrambi i membri dell'equazione;
controllare se n è pari o dispari: se n è dispari, le soluzioni dell'equazione ottenuta sono
le stesse dell'equazione irrazionale; se n è pari, possiamo eseguire il controllo delle soluzioni
mediante verifica.
Esempio
x 2 3x 6 2x 6
Elevando entrambi i membri al quadrato otteniamo
3x 2 24 x 36 0
che ci dà come soluzione x1 7 ; x2 2 .
Questi valori saranno anche soluzione dell'equazione di partenza?
Per verificarlo sostituiamo 7 e 2 nell'equazione irrazionale data.
Sostituiamo x=7
Primo membro
Secondo membro
49 21 6 8
27 6 8
Ora sostituiamo x=2
466 2
2(2) 6 2
Nel secondo caso, poiché i due membri dell'equazione non hanno lo stesso valore, la radice x=2 non
è soluzione dell'equazione irrazionale.
N.B.: C'è un altro metodo per verificare quali soluzioni sono accettabili? Si, bisogna imporre la non
negatività del radicando e del secondo membro, ottenendo così la condizione x 3 …..Controlla tu!
DISEQUAZIONI IRRAZIONALI
Le disequazioni irrazionali del tipo
disequazioni:
A( x) B( x) sono equivalenti a un sistema di tre
B( x) 0
A( x) B( x) A( x) 0
A( x) [ B( x)] 2
Mentre le disequazioni irrazionali del tipo A( x) B( x) hanno come insieme di soluzione
l'unione degli insiemi delle soluzioni di due sistemi, ognuno di due disequazioni:
B( x) 0 B( x) 0
A( x) B( x)
2
A
(
x
)
0
A( x) [ B( x)]
Esempio
25 x 2 x 1
2
(oppure x 1 25 x )
La disequazione ha senso quando
25 x 2 0
x 1 0
25 x 2 ( x 1) 2
N.B.: La prima condizione è necessaria perché esista la radice, la seconda perché se x 1 la
disuguaglianza in questione non sarà mai verificata (perché si chiede che una quantità positiva al
primo membro sia di una quantità negativa al secondo membro!).
Si ottiene quindi, dopo brevi passaggi,
5 x 5
x 1
x 2 x 12 0
Le soluzioni accettabili sono quindi 4 x 5 .
Potrebbe essere utile provare a fare i grafici di
25 x 2 , x 1, ( x 1) 2
per capire la discussione algebrica del sistema.
Esercizi
1. 1. Risolvere le seguenti equazioni irrazionali, controllando l'accettabilità delle soluzioni.
2 x 5 3( x 1)
2
[Perché la soluzione 9 non è accettabile?]
3x( x 2) 1 ( x 1)2 x
[0; -4]
1
2
x(3x 1) (1 3x)
5
3
[-5]
2x 6 x 2 x 2
[Perché la soluzione 13 non è accettabile?]
2
(dopo aver elevato al quadrato due volte, si ottiene 3 x 4 ….)
1
[0; 4 ]
2x x
2. 2. Risolvere le seguenti disequazioni irrazionali, seguendo lo schema di teoria in sintesi per
verificare l'accettabilità delle soluzioni, ed aiutandoti con il grafico.
x 3x 2 x
0 x
x 1 3x 1
1
3 x 0
2
2
3
N.B.: il grafico riassuntivo di questa disequazione irrazionale è il seguente
-1
x 1 5 x 6
1
3
0
x 3
Sistemi: rette e sistemi lineari, sistemi di grado
superiore al primo, sistemi di disequazioni
Teoria in sintesi
Alcuni richiami utili
La distanza tra due punti A( x A ; y A ) e B( xB ; y B ) è data da
AB ( x B x A ) 2 ( y B y A ) 2
(farsi un disegno per capire che si usa il teorema di Pitagora)
L’equazione generale della retta è del tipo
ax by c 0
(forma implicita)
Il punto medio del segmento AB è dato da
x xB y A y B
M A
;
2
2
y mx q 0
(forma esplicita)
x 0
y
y
q
.
con m coefficiente angolare e q intercetta asse
y 4 x q è il fascio improprio di rette parallele con coefficiente angolare m=4
y y1 m( x x1 ) è il fascio proprio di rette passanti per lo stesso punto P( x1 ; y1 )
L’equazione della retta passante per due punti
P( x1 ; y1 ) e Q( x2 ; y2 ) è data da:
Il coefficiente angolare delle rette passanti per A e B è dato da
y yA
m B
xB x A
y y1
x x1
y 2 y1 x2 x1
Osserva: per convincerti che la formula è giusta, basta osservare che:
1. l’equazione data rappresenta effettivamente una retta;
2. i punti P e Q stanno effettivamente sulla retta, in quanto le loro coordinate soddisfano
l’eguaglianza.
La distanza di un punto P( x0 , y 0 ) da una retta r di equazione ax bx c 0 è data da
d
ax0 by0 c
a2 b2
SISTEMI LINEARI
Un sistema di equazioni è un insieme di due o più equazioni. E’ detto lineare se è composto da
equazioni di primo grado.
Se studiamo il problema in termini geometrici, le equazioni del sistema vengono rappresentate, nel
piano cartesiano, da rette.
La soluzione di un sistema è una soluzione comune a tutte le equazioni che lo compongono.
Il sistema di due equazioni in due incognite, ridotto alla forma normale, è
ax by c
a1 x b1 y c1
(1)
Un sistema è determinato, impossibile o indeterminato a secondo che abbia UNA, NESSUNA o
INFINITE soluzioni.
Il sistema (1) è
-
-
-
-
determinato se ab1 a1b
indeterminato se ab1 a1b ; bc1 b1c
-
-
impossibile se ab1 a1b ; bc1 b1c
Queste possibilità si traducono geometricamente nelle seguenti. Se il sistema è:
determinato, le due rette si intersecano in un punto e quindi sono incidenti;
indeterminato, le due rette sono coincidenti;
impossibile, le due rette sono parallele.
Provare a vedere che la eguaglianza ab1 a1b significa proprio
che le due rette hanno stesso coefficiente angolare (quindi sono
o parallele e distinte, o coincidenti).
Richiamiamo brevemente lo schema risolutivo del metodo di sostituzione con un semplice esempio.
2 x y 0 2 x (6 x 8) 0
6 x y 8
y 6x 8
8 x 8
x 1
y 6 x 8 y 2
Esercizi
1. 1. Risolvere i seguenti sistemi, rappresentando graficamente le rette che li compongono.
x y 3
;
2 x y 6
x y 3
3x 3 y 9
x y 3
x y 2
[incidenti nel punto A(1,4), coincidenti, parallele]
2. 2. Risolvere usando il metodo di sostituzione o quello del confronto.
4 x y 5
;
3x 2 y 12
x y 0
;
2 x 3 y 1 0
8 x 2 y 10
3x 2 y 12
y 2x 1
6 x y 1
3. 3. Risolvere i seguenti sistemi simmetrici e non:
x y 7
2
2
x y ( x y) 32
[4,3; 3,4]
x y 4
7 xy 9
[impossibile]
x y 16
xy 10
[8 54 , 8 54 ;....]
2
2
2
N.B.: Ricorda: x y ( x y) 2 xy
x y 5
;
xy 6
[3,2; 2,3]
x2 y 2 1 0
x y 6
[impossibile]
x 2 y 2 10
x y 4
[1,3; 3,1]
SISTEMI DI DISEQUAZIONI
Per risolvere una disequazione fratta
A( x)
0
B( x)
si studiano separatamente i segni del numeratore (N) e del denominatore (D), poi si determina il
segno della frazione utilizzando la regola dei segni.
La frazione si annulla se e solo se il numeratore è 0; non esiste se il numeratore è nullo.
Esempio
x 1
0;
x2
N 0; x 1 0; x 1
D 0 ; x 2 0 ; x 2
-2
1
D>0
N>0
+
-
le soluzioni sono quindi x 2
+
x 1
Per risolvere un sistema di disequazioni si risolvono le singole disequazioni; poi si determina in
quali intervalli sono verificate contemporaneamente tutte le disequazioni.
Lo schema può essere il seguente:
A( x) 0
B( x) 0
C ( x) 0
Esempio
x 2
x 2 0
2
x 4
x x 12 0 x 3
x 1 0
x 1
-4
-1
1a
2a
3a
2
3
111a
2a
3a
1
Sistema impossibile.
Appendice 1
SISTEMI DI GRADO SUPERIORE AL PRIMO, SISTEMI OMOGENEI
Il grado di un sistema è dato dal prodotto dei gradi delle sue equazioni. Per esempio
4
5 x y 2
2
2 xy 3 x
( grado 4)
( grado 2)
4 2 8)
( grado
I sistemi di secondo grado si possono risolvere con il metodo di sostituzione, di confronto, di
riduzione.
Un sistema di secondo grado nelle due incognite x e y è simmetrico quando non cambia la sua forma
se al posto di x mettiamo y e viceversa.
Risolviamo due tipi particolari di sistema simmetrico di secondo grado
xy p
x y s
che si risolve mediante l’equazione ausiliaria
t 2 st p 0.
x 2 y 2 a
x y s
riconducibile al primo caso ponendo
x 2 y 2 ( x y) 2 2 xy.
La risoluzione dei sistemi simmetrici di quarto grado del tipo
xy p
2
2
x y a
si riconduce al primo caso dei sitemi simmetrici di secondo grado, utilizzando il seguente
accorgimento relativo ai prodotti notevoli
x 2 y 2 ( x y) 2 2 xy.
Il sistema omogeneo
ax 2 bxy cy 2 0
2
a x b xy c y 2 0
ha come soluzione la coppia (0;0).
Per trovare altre eventuali soluzioni bisogna ricorrere alla sostituzione y tx e risolvere le
equazioni di secondo grado in t, scegliendo le soluzioni comuni.
Per risolvere il sistema
2
2
ax bxy cy 0
2
2
a x b xy c y d
d 0
si opera la sostituzione y tx in entrambe le equazioni e si ottiene un sistema nell’incognita t.
Il sistema
2
2
ax bxy cy d
2
2
a x b xy c y d
d 0
d 0
è riconducibile al caso precedente utilizzando il metodo di riduzione.
Esempi
1. 1.
x 2 y 2 5
x y 1
( x y) 2 2 xy 5
x y 1
(1) 2 2 xy 5
x y 1
2 xy 4
x y 1
xy 2
x y 1
Equazione ausiliaria
t2 t 2 0
t1 2
t2 1
Il sistema ha quindi come soluzioni
x 2
y 1
2. 2.
x 1
y 2
2 x 2 xy y 2 0
2
6 x xy y 2 0
Con le sostituzioni y = tx otteniamo, dopo semplici passaggi,
2 t t 2 0
6 t t 2 0
Cerchiamo le soluzioni eventuali in comune.
La prima equazione ha soluzione
2
t
1
La seconda
2
t
3
Sostituendo l’unica soluzione in comune in y = tx, otteniamo
y = -2x
Il sistema è quindi indeterminato ed ammette infinite soluzioni del tipo
(a;2a) , con a R.
Le coniche: circonferenza, parabola, ellisse e
iperbole.
Teoria in sintesi
Queste curve si chiamano coniche perché sono ottenute tramite l’intersezione di una superficie
conica con un piano.
Si possono definire tutte come luoghi geometrici e, di conseguenza, ricavarne l'equazione algebrica
che le rappresenta nel piano cartesiano.
Lo vedremo come esempio per la circonferenza.
LA CIRCONFERENZA
La circonferenza è il luogo geometrico dei punti
equidistanti da un punto C, detto centro.
Si ottiene tagliando un cono con un piano
perpendicolare al suo asse.
La distanza fra ognuno dei suoi punti e il centro
è il raggio della circonferenza.
Note le coordinate del centro C (;) e la misura r del raggio, l'equazione della circonferenza è
allora
(x )2 ( y )2 r 2
(equazione canonica)
Ricaviamola.
Tutti i punti P che stanno sulla circonferenza hanno la proprietà comune che
PC r , cioè PC r 2
2
Utilizzando la formula della distanza tra due punti si ottiene allora
PC ( x ) 2 ( y ) 2
Elevando al quadrato e sostituendo al posto di PC
cercata.
2
la sua misura si ottiene allora l'equazione
Esempio
( x 2) 2 ( y 1) 2 9 è l’equazione della circonferenza con centro C(2; -1) e raggio 3.
L’equazione può anche essere scritta nella forma
x 2 y 2 ax by c 0,
(equazione generale)
dove a, b e c sono legati alle coordinate del centro C ( ; ) ed al raggio dalle seguenti relazioni:
a ,
2
b
,
2
2
2
a
b
r c ,
2 2
a 2
b 2
c 2 2 r 2
Esempio
x 2 y 2 2 x 4 y 1 0 è l’equazione della circonferenza con centro C(-1,2) e raggio 4.
Si segnalano i seguenti casi particolari
a=0, il centro appartiene all’asse y:
b=0, il centro appartiene all’asse x;
c=0, la circonferenza passa per l’origine degli assi.
N.B.: Verificalo!
Per determinare l’equazione di una circonferenza è necessario determinare i tre parametri (a, b, c)
dell’equazione generale di una circonferenza.
Ad esempio citiamo i seguenti casi:
sono note le coordinate del centro e il raggio;
sono note le coordinate degli estremi di un diametro;
la circonferenza passa per un punto e sono note le coordinate del centro;
la circonferenza passa per tre punti non allineati;
la circonferenza passa per due punti e il centro appartiene a una retta nota;
sono note le coordinate del centro e la circonferenza è tangente a una retta nota.
N.B.: Lo studente è invitato a verificare graficamente con degli esempi che queste condizioni sono
sufficienti per disegnare circonferenze.
Vediamo un esempio per chiarire le idee.
Esempio
Determinare l’equazione della circonferenza di centro C(2,-3) e passante per A(1,1).
Il raggio della circonferenza sarà:
r CA 12 (4) 2 17
(perchè? Cosa stiamo utilizzando?)
Usando l’equazione canonica della circonferenza otteniamo
x 2 y 2 4 x 6 y 35 0
Una retta ed una circonferenza possono essere secanti, tangenti o esterne l'una rispetto all'altra.
Dato allora il sistema formato dalla equazione della circonferenza e da quella della retta
x 2 y 2 ax by c 0
ax by c 0
nell'equazione di secondo grado che risolve il sistema (ricavando una delle due variabili in funzione
dell’altra nella seconda equazione), abbiamo allora le tre possibilità alternative:
0 , la retta è secante;
0 , la retta è tangente;
0 , la retta è esterna.
(Spiega perchè)
2
2
Dato un punto P( x0 ; y 0 ) e una circonferenza di equazione x y ax by c 0 , si possono
verificare le tre condizioni.
P è esterno alla circonferenza, le rette per P tangenti alla circonferenza sono due;
P appartiene alla circonferenza, la retta tangente è una sola;
P è interno alla circonferenza, non esistono rette tangenti uscenti da P.
Per determinare le equazioni delle eventuali rette tangenti, si possono seguire due metodi.
I METODO
si scrive l'equazione del fascio di rette passanti per P( x0 , y 0 )
y y0 m( x x0 );
si scrive il sistema fra le equazioni del fascio e la circonferenza:
y y 0 m( x x 0 )
;
2
2
x y ax by c 0
y y 0 m( x x 0 )
2
2
x ( y 0 m( x x0 )) ...
con il metodo di sostituzione si ottiene quindi un'equazione di secondo grado nella variabile
x;
si impone la condizione di tangenza, ossia 0 ;
si risolve l'equazione di secondo grado rispetto a m;
se m1 m2 , le rette tangenti sono due e il punto P è esterno alla circonferenza;
se m1 m2 , la retta tangente è una sola e il punto P appartiene alla circonferenza;
se m1 , m2 R, non esistono rette tangenti e il punto P è interno alla circonferenza;
si sostituisce il valore o i valori trovati di m nell'equazione del fascio di rette.
N.B.: E’ sempre conveniente controllare graficamente i risultati ottenuti…!
Esempio
2
2
Scrivere l'equazione delle rette passanti per P(0,-4) e tangenti alla circonferenza x y 4 .
L'equazione della retta generica passante per P è:
y (4) m( x 0)
intersecando con la circonferenza otteniamo
y mx 4
;
2
2
x
y
4
y mx 4
2
2
x (1 m ) 8mx 12 0
0
imponendo 4
si ottiene
(4m) 2 12(1 m 2 ) 0
4
che ci dà coefficiente angolare delle rette tangenti m 3 .
Le due rette quindi:
y 3x 4
N.B.: Verifica tu graficamente (disegna circonferenza e rette tangenti) i risultati ottenuti.
II METODO
si determinano le coordinate del centro C e del raggio r della circonferenza;
si scrive l’equazione del fascio di rette passanti per P( x0 , y 0 )
y y0 m( x x0 ) ,
cioè
mx y y0 mx0 0 ;
si applica la formula della distanza fra le rette e il centro C;
si pone tale distanza uguale al raggio e si risolve l’equazione in m;
si sostituisce il valore o i valori trovati di m nell’equazione del fascio di rette.
Se il punto P appartiene alla circonferenza, allora la retta tangente è la retta per P perpendicolare a
PC.
N.B.: Applica tu il secondo metodo all’esempio appena visto.
Due circonferenze possono essere secanti in due punti, tangenti in uno stesso punto (esternamente o
internamente), una interna all'altra, concentriche o esterne.
Per determinare gli eventuali punti di intersezione o il punto di tangenza, occorre risolvere il
sistema formato dalle equazioni delle due circonferenze.
2
2
x y ax by c 0
2
2
x y a x by c 0
E' conveniente risolvere il sistema con il metodo di riduzione.
Sottraendo le due equazioni, si ottiene infatti l'equazione di primo grado
(a a ) x (b b) y (c c ) 0
che è l’asse radicale, nella quale si potrà ricavare x in funzione di y (per esempio) e sostituirla poi in
una delle due equazioni della circonferenza.
LA PARABOLA
La parabola è il luogo geometrico dei punti
equidistanti da una retta (direttrice) e da un
punto (fuoco). La retta passante per il fuoco e
perpendicolare alla direttrice si chiama asse
della parabola.
L'asse della parabola è un asse di simmetria e
interseca la parabola nel vertice.
Una parabola con asse parallelo all'asse y è
rappresentata da un'equazione del tipo
y ax 2 bx c
(con a0).
Concavità e apertura della parabola dipendono dal parametro a.
Riassumiamo alcune caratteristiche della parabola nel seguente schema.
Per i casi particolari (b=0; c=0; b=c=0) lo studente è invitato a completare lo schema riassuntivo.
Equazione y ax bx c
Asse
b
x
2a
Vertice
b
V
;
2a 4a
Fuoco
b 1
F
;
2a 4a
Direttrice
1
y
4a
2
PARABOLE
y ax c(b 0)
y ax 2 bx(c 0)
y ax 2 (b c 0)
x=?
x=?
x=?
V?
V?
V=O (perché?)
F?
F?
F?
y= ?
y= ?
y= ?
2
Figure
N.B.: Invitiamo lo studente a costruire lo schema riassuntivo della parabola nel caso in cui essa
abbia asse parallelo all'asse y.
Come ben sai l'equazione di una parabola con asse parallelo all'asse x è del tipo
x ay 2 by c
(con a0).
dove a, b, c sono coefficienti reali e a0.
Ricorda, basterà scambiare tra loro le ascisse con le ordinate….! Perché?
2
Anche nell'equazione della parabola (come in quella della circonferenza) y ax bx c (o
x ay 2 by c ) sono presenti i tre coefficienti a, b e c. Per poterli determinare occorrono in
genere tre condizioni.
Alcune possibili condizioni sono le seguenti:
sono note le coordinate del vertice e del fuoco;
sono note le coordinate del vertice (o del fuoco) e l'equazione della direttrice;
la parabola passa per tre punti non allineati;
la parabola passa per due punti e si conosce l'equazione dell'asse;
la parabola passa per un punto e sono note le coordinate del vertice (o del fuoco);
la parabola passa per un punto e sono note le coordinate dell'asse e della direttrice.
N.B.: Per le soluzioni di problemi di tangenza o intersezione tra rette e parabola ed esercizi
riguardanti la determinazione dell’equazione della parabola (cioè dei suoi parametri a, b, c)
soddisfacente tre condizioni date, si procederà nello stesso modo e con le stesse procedure utilizzate
nel caso della circonferenza.
A titolo di esempio riportiamo solo lo schema riguardante le condizioni di tangenza tra retta e
parabola.
Le rette tangenti a una parabola, uscenti da un punto P( x0 , y 0 ) , possono essere due, una o
nessuna.
Per determinare le equazioni delle eventuali rette passanti per P( x0 , y 0 ) e tangenti alla parabola,
si procede nel seguente modo:
si scrive l'equazione del fascio di rette passanti per P( x0 , y 0 ) ,
y y0 m( x x0 ) ;
si scrive il sistema fra le equazioni del fascio e della parabola:
y y 0 m( x x0 )
2
y ax bx c
si perviene all'equazione di secondo grado in x:
ax 2 (b m) x (c mx0 y 0 ) 0;
si calcola :
(b m) 2 4a(c mx0 y 0 ) ;
si pone la condizione di tangenza, ossia 0 :
(b m) 2 4a(c mx0 y 0 ) 0 , ossia m 2 2m(b 2ax0 ) (b 2 4ac 4ay 0 ) 0 ;
si risolve l'equazione di secondo grado rispetto a m:
-
-
-
-
se m1 m2 , le rette tangenti sono due;
se m1 m2 , la retta tangente è una sola e il punto P appartiene alla parabola;
l’equazione non ha soluzioni.
se si trova il valore (o i valori) di m, si sostituisce nell'equazione del fascio di rette
determinando così le equazioni delle rette tangenti.
Per l’ellisse e l’iperbole richiamiamo solo brevemente la forma delle loro equazioni, e le relazioni
che legano le coordinate dei punti caratteristici per la loro determinazione come luoghi geometrici.
ELLISSE
Equazione dell’ellisse riferita al centro degli assi cartesiani
x2 y2
1
a2 b2
centro O(0,0)
fuochi F1 (c,0) e F2 (c,0) , essendo
c2 a2 b2
vertici A(a,0), B(b,0), -A, -B
e
c
a2 b2
a
a
N.B.: L’eccentricità e indica la forma più o meno schiacciata dell’ellisse: 0 e 1 . Quanto vale
nella circonferenza?
IPERBOLE
Equazione dell’iperbole riferita al centro degli assi cartesiani
x2 y2
1
a2 b2
centro O(0,0)
fuochi F1 (c,0) e F2 (c,0) , essendo
c2 a2 b2
vertici A(a,0), B(-a,0)
b
y x
a
asintoti
c
a2 b2
a
a
Per l’iperbole è e 1.
e
Esercizi
1. 1. Disegnare, dopo aver ricavato centro e raggio, le seguenti circonferenze.
x2
x2
x2
x2
y 2 2 x 4 y 11 0
y 2 8x 9 0
y 2 2x 0
y2 x y 5 0
[N.B.: non è una circonferenza, perchè?]
x ( y 2) 9 0
16 x 2 16 y 2 24 x 32 y 7 0
2
2
[N.B.: Ricorda, devi dividere per 16! Perchè?]
2. 2. Trovare l’intersezione tra retta e circonferenza e rappresentarle graficamente.
x 2 y 2 3x 3 y 2 0
3x 2 y 1 0
[A (1; 2) e B (-1; -1)]
3. 3. Determinare l’equazione della circonferenza avente per diametro il segmento di estremi A(3; 1) e B(2; 5).
[N.B.: Il centro è il punto medio del segmento AB ed il raggio si ottiene utilizzando la formula
2
2
della distanza tra due punti. La circonferenza cercata è x y x 6 y 1 0 ]
4. 4. Determinare l’equazione della circonferenza passante per A(2; 0); B(-1; 0) e C(1; 2).
[N.B.: Basta risolvere il sistema
4 0 2a 0 c 0
1 0 a 0 c 0
1 4 a 2b c 0
x2 y2
per ottenere
(perchè?)
5
1
8
x y 0
3
3
3
]
5. 5. Stabilire se i punti A(1; 5); B(10; 2); C(-1; -2) appartengono o meno alla circonferenza di
equazione
x 2 y 2 10 x 4 y 4 0
[si, si, no]
2
2
6. 6. Determinare l’equazione delle rette tangenti alla circonferenza x y 8x 6 y 0 nei
punti O(0; 0) e A(0; 6).
[N.B.: Sono le intersezioni della circonferenza con l’asse delle y. Basterà sfruttare il fatto che il
raggio della circonferenza è perpendicolare alla retta tangente nei suoi punti di tangenza….
4x 3 y 0 ;
4x 3 y 18 0 ]
7. 7. Determinare gli eventuali punti di intersezione delle due circonferenze e rappresentarli
graficamente.
2
2
x y 10
2
2
x y 8 x 16 y 30 0
[N.B.: Ricorda, usa il metodo di riduzione sottraendo….A(-1; 3); B(3; 1)]
8. 8. Data la parabola di equazione
y x 2 3x 4
determinare le sue intersezioni con gli assi cartesiani e disegnarla.
Determinare poi i punti di intersezione con la prima bisettrice (y = x)
x1, 2 2 2 2
y1, 2 ?
9. 9. Determinare l’equazione della parabola di vertice V(1; 0) e direttrice d: y = 2.
Rappresentarla graficamente
1 2 1
1
y 8 x 4 x 8
10. 10. Determinare l’equazione della parabola passante per i punti A(-1; 0); B(0; 5); C(2; 3).
0 a b c
5 c
[Basta risolvere il sistema 3 4a 2b c ]
11. 11. Stabilire se la retta di equazione
y = x-4
è secante, tangente o esterna alla parabola di equazione
y x 2 3x 4
[secante in A(4; 0) e B(?; ?)]
2
12. 12. Data la parabola di equazione y x 2 x 3 , determinare le equazioni delle rette
passanti per P(0; -1).
[Puoi risolvere, imponendo il 0 , il sistema
y mx m
2
y x 2x 3
ottenendo m 2 2 ]
13. 13. Disegna l’ellisse di equazione
x2 y2
1
36 9
[a = ? ; b = ?]
14. 14. Disegna l’iperbole di equazione
x2 y2
1
16 9
[che equazione hanno gli asintoti?]
Esponenziali e logaritmi
Teoria in sintesi
ESPONENZIALI
Potenze con esponente reale
x
La potenza a è definita:
se a 0,
per ogni x R ;
se a 0,
per tutti e soli gli x R ;
se a 0,
per tutti e soli gli x Z .
Sono definite:
3 3 3 ;
2
2
73
3 72 ;
1
3 2
.
3 2
Non sono definite:
2 ;
0 0 ; 0 3 .
3
Casi particolari :
a 1 , 1x 1 , per ogni x R ;
x 0 , a 0 1 , per ogni a R ;
Le proprietà delle potenze definite per esponenti interi valgono anche per esponenti reali:
Se a 0, per ogni x, y appartenen ti a R vale :
1.
a
x y
a x y ;
2. a x a y a x y ;
3. a x : a y a x y ;
4.
a b x
ax bx ;
x
5. a
x
1
1
x
a
a
Funzione esponenziale
Si chiama funzione esponenziale ogni funzione del tipo :
y a x , con a 0 fissato,
x R.
Il dominio della funzione, cioè l'insieme dei valori che si possono attribuire a x è tutto R ;
il codominio, cioè l'insieme dei valori che la funzione assume è R+ (la funzione esponenziale
è sempre strettamente positiva).
Si distinguono tre casi:
a 1 :
funzione crescente :
x y ax ay ;
a 1 :
funzione costante :
a x 1 per ogni x R ;
0 a 1 :
x
y
funzione decrescente : x y a a .
I seguenti grafici illustrano il comportamento della funzione esponenziale nei vari casi :
y
y = ax
x
y=a
y = ax
1
x
y=1
0
0<a<1
;
a>1
;
a>1
x
;
a>a
EQUAZIONI ESPONENZIALI E LOGARITMI
Un'equazione si dice esponenziale quando l'incognita compare soltanto nell'esponente
di una o più potenze.
L'equazione esponenziale più semplice (elementare) è del tipo :
a x b , con a 0 e b 0 ; x è l' incognita dell' equazione .
x
Un'equazione esponenziale del tipo a b può essere impossibile, indeterminata o determinata :
se b 0, oppure b 1 e a 1 ;
impossibile
indeterminata se a 1, b 1 ;
determinata
se a 0, a 1, b 0 ;
esempio : 2 x 3 oppure 1 x 5 ;
esempio : 1 x 1 ;
esempio : 3 x 5 .
Si chiama logaritmo in base a di b l'unica soluzione dell'equazione esponenziale elementare
a
x
= b
a = base dell’eponenziale
e del logaritmo
x = log a b
nel caso determinato, cioè l'esponente x da assegnare alla base a per ottenere il numero b .
Supponiamo di dover risolvere un'equazione esponenziale a b :
se a e b si scrivono come potenze (razionali) della stessa base, si eguagliano gli esponenti :
x
2x 8
2 x 23
x 3;
se a e b non si scrivono come potenze (razionali) della stessa base, le soluzioni si scrivono
x
sotto forma di logaritmi : 2 3
x log2 3 .
Il logaritmo risulta essere l'operazione inversa dell'esponenziale, pertanto le limitazioni cui
è soggetto l'esponenziale si riflettono sul logaritmo: fissata la base a>0 , deve essere b>0 ,
0
1
inoltre valgono i casi particolari: loga 1 0 , poichè a 1 ; loga a 1 , poichè a a .
Analogamente, alle proprietà degli esponenziali precedentemente elencate corrispondono
le seguenti proprietà dei logaritmi:
1) log a x y y log x
( x R ; y R , a 0) ;
2) log a x y log a x log a y
( x R ; y R , a 0);
x
log a x log a y
y
log c b
4) log a b
log c a
( x R ; y R , a 0) ;
3) log a
(a, b, c 0); formula di cambiament o di base nei logaritmi .
I logaritmi che compaiono sulle calcolatrici sono in base a 10 oppure in base a e 2,718 :
log x indica il log10 x , detto anche logaritmo decimale; ln x , indica il log e x , detto anche
logaritmo naturale o neperiano.
Funzione logaritmica
Si chiama funzione logaritmica ogni funzione del tipo :
y loga x , con a 0 e a 1 fissato,
x R.
La funzione logaritmica è l'inversa dell'esponenziale, pertanto dominio e codominio
risultano scambiati rispetto a quelli della funzione esponenziale.
Il dominio della funzione, cioè l'insieme dei valori che si possono attribuire a x è R+ ;
il codominio, cioè l'insieme dei valori che la funzione assume è R .
Si distinguono due casi:
x y log a x log a y ;
a 1 :
funzione crescente :
0 a 1 :
funzione decrescente : x y log a x log a y ;
y
y = log a x
y = log a x
0
1
x
y = log x
a
0<a<1
;
a>1
;
a>1
;
a>a
I grafici della funzione logaritmica si ottengono da quelli della funzione esponenziale
per simmetria rispetto alla bisettrice del I e III quadrante ( y x ) ; essi illustrano
il comportamento della funzione esponenziale nei vari casi :
EQUAZIONI LOGARITMICHE
Un'equazione si dice logaritmica quando l'incognita compare soltanto nell'argomento
di uno o più logaritmi.
L'equazione logaritmica più semplice (elementare) è del tipo :
log a x b , con a 0 e b R ; x 0 è l' incognita dell' equazione .
b
La sua soluzione, per quanto detto a proposito dell'equazione esponenziale, è : x a .
Per risolvere un'equazione logaritmica conviene:
1. 1.
(quando è possibile) trasformare l'equazione data in una equivalente del tipo
log a A x log a B x , applicando le proprietà dei logaritmi ;
2. 2. determinare le soluzioni dell'equazione A x B x ;
3. 3. eseguire il controllo mediante verifica diretta dei valori di x calcolati al punto 2 ;
4. 4. in alternativa al punto 3, associare all'equazione di cui al punto 2 tutte le condizioni
di esistenza sui logaritmi (ricordiamo che un logaritmo è definito soltanto per
valori positivi del suo argomento), per selezionare le soluzioni accettabili.
Esempi
1. 1. Risolviamo l'equazione:
8 2 x 1 2 x 1 16 .
Osserviamo che:
2 x 1 2 x 2 e
2 x 1
2x
.
2
Quindi è possibile trasformare l'equazione assegnata nell'equazione:
8
2x
2 2 x 16
2
2x 8
2 x 23
La soluzione dell'equazione data è quindi x 3.
2. 2. Risolviamo l'equazione:
5 3x 7 .
Possiamo trasformare l'equazione eseguendo il logaritmo (in una base qualsiasi, per esempio in
base 10) del primo e del secondo membro:
log 5 3 x log 7 .
Applichiamo la proprietà 2) dei logaritmi:
log 5 log 3 x log 7 .
Applichiamo la proprietà 1) dei logaritmi:
log 5 x log 3 log 7 .
Isolando x otteniamo:
x
log 7 log 5
log 3
(*) .
x
In alternativa potevamo isolare 3 , ottenendo:
3x
7
5.
Prendendo il logaritmo in base 3 di entrambi i membri si ha:
x log3
7
log3 7 log3 5
5
Utilizzando la formula di cambiamento di base 4) si riottiene (*).
3. 3. Risolviamo l'equazione:
2 x 2 3 x 6 .
Osserviamo che:
2 3 x
23
2x .
L'equazione assegnata è equivalente a:
2x
8
6
2x
2x 2 x 8 6 2 x
2x
2x
Il denominatore, essendo una funzione esponenziale, non può assumere il valore zero. Possiamo
moltiplicare per 2 x entrambi i membri, ottenendo:
2
x 2
6 2x 8 0.
E' evidente la struttura di equazione algebrica di II grado nell'incognita 2 x .
x
Risolvendo tale equazione (può essere utile introdurre una variabile ausiliaria z 2 per rendere
più evidente la natura di equazione di secondo grado) si ha:
2 x 2 oppure 2 x 4
da cui:
x 1
oppure x 2 .
4. 4. Risolviamo l'equazione logaritmica:
log 3 x 1 log 3 x 2 log 3 x 2 .
Imponiamo le condizioni di esistenza sui logaritmi dell'equazione data, ricordando che
gli argomenti devono essere positivi:
x 1 0
x 2 0
x 0
x 1
x2
x0
x2
cioè alla variabile x si possono assegnare solo i valori maggiori di 2.
Risolviamo l'equazione applicando la proprietà 3) dei logaritmi e osservando che 2 log3 3 :
2
x 1
x
log3
log3 2
x 2
3
Uguagliando gli argomenti si ha la seguente equazione equivalente:
x 1 x
x2 9
x
x 2 11 x 9 0
x1,2
11 157
2
.
11 157
2
è minore di 2, quindi non è compatibile con le condizioni
Il valore
di esistenza. L'unica soluzione dell'equazione è data da:
x
11 157
2
.
Esercizi
m
1. 1. Tenendo presente che
n
x m x n , scrivi le seguenti potenze sotto forma di radice:
5
38 ;
3
2
43;
12
;
3
a) a)
2
4
3;
2
1 3
;
4
b) b)
2
11 5
.
3
2. 2. Scrivi le seguenti radici sotto forma di potenza con esponente razionale:
a) a)
6
25 ;
1
b) b)
4
2
4
;
243 ;
19
1
;
256
4
0.25 ;
7
1
.
125
3. 3. Risolvi le seguenti equazioni esponenziali:
2 x 16 2
9
2
8x 2 4x
1
2
a) a)
b) b)
a x a 2 x 1
a
c) c)
x 1
d) d)
2 2
e) e)
4 2 2
x
x
5
6
a2
2
x 1
7
x
7 log 7 log 3
log5
3
log 5
3 5x 7
f) f)
g) g)
3 x 31x 4
h) h)
3 2 x 9 3 x 3 3 x 1
log 3
1;
log 2
2 2 x 3 25 2 x 3 0
3; log2 3
4. 4. Risolvi le seguenti equazioni logaritmiche:
a) a)
b) b)
c) c)
d) d)
log 2 x 1 3
9
log x 2 log 5 log x
log x 2 log x 1 log 5
5
2
2 log 2 x 2 log 2 x 3
6
log x 1 2 log x 1 log 8 2
3
2 ; 9
e) e)
log3 x 1
f) f)
0; 1
1; 2
6 2 x 2x 5
i) i)
j) j)
14
log2 5
1
log3 x
2
3 5
2
Trigonometria
Teoria in sintesi
Radiante: angolo al centro di una circonferenza che sottende un arco di lunghezza rettificata uguale
al raggio
Si passa dai gradi ai radianti con la seguente proporzione: : 180° = rad :
Considerato un sistema di riferimento cartesiano si definisce circonferenza goniometrica la
circonferenza avente centro nell’origine e raggio unitario (circonferenza di equazione x 2 + y2 =1).
Il punto A(1,0) è detto origine degli archi, il verso di percorrenza positivo è quello antiorario.
Notiamo anche che la misura in radianti dell’angolo al centro coincide con la misura dell’arco della
circonferenza goniometrica sotteso, quindi in trigonometria si parla indifferentemente di archi o di
angoli.
Detto l’angolo al centro AOˆ B definiamo ora le seguenti funzioni trigonometriche:
sen = ordinata del punto B secondo estremo dell’arco (il primo estremo è in A) = BH .
cos = ascissa del punto B secondo estremo dell’arco = OH .
tg tanrapporto, quando esiste, tra il seno e il coseno dell'angolo (cioè quando cos 0)
cotg cotanrapporto, quando esiste, tra il coseno e il seno dell'angolo (cioè quando
sen 0).
N.B. Dalle definizioni date segue che seno coseno tangente e cotangente sono funzioni di , cioè
sono numeri reali che dipendono solamente dal valore dell’angolo
RELAZIONI
FONDAMENTALI
FRA LE
DIVERSE
FUNZIONI
TRIGONOMETRICHE DI UNO STESSO ANGOLO ORIENTATO:
Tra le funzioni trigonometriche viste intercorrono le seguenti relazioni:
sen 2 cos 2 1
(teorema di
Pitagora)
sen
cos
1
cos
cotg
tg sen
tg
Si può inoltre dimostrare che tg è l’ ordinata del punto T di intersezione tra la tangente
geometrica alla circonferenza nel punto A e la semiretta OT (che teorema sui triangoli si usa?).
Nota la funzione trigonometrica di un angolo è possibile ricavare le altre, e, dalle relazioni
precedenti si ottiene l’espressione di tutte le funzioni di un dato angolo orientato mediante una sola
di esse
N.B. Il segno va scelto a seconda del quadrante in cui si trova l’angolo
sen
cos
tg
sen
sen
1 sen2
cos
1 cos2
cos
NOTO
tg
cctg
sen
1 sen2
1 cos2
cos
tg
1
1 tg 2
1 tg 2
1
ctg
1 ctg 2
1 ctg 2
tg
1
ctg
VALORI DELLE FUNZIONI GONIOMETRICHE DI ARCHI PARTICOLARI
sen
cos
15° = /12
6 2
4
6 2
4
18° = /10
5 1
4
10 2 5
4
30° = /6
1/2
45° = /4
2 /2
60° = /3
3 /2
tg
2 3
52 5
5
3 /3
3 /2
2 /2
1
3
1/2
90° = /2
1
0
non esiste
180° =
0
-1
0
270° = 3/2
-1
0
non esiste
0° = 360° = 2
0
1
0
Da evidenti simmetrie sulla circonferenza si deducono poi i valori delle funzioni trigonometriche di
altri archi particolari.
Esempio
il coseno di 4/3 è uguale in modulo a quello di 3 (infatti 4/3 , essendo nel terzo
quadrante però il suo segno è negativo, quindi cos 4/3
Esercizi
1.1.
Dopo
aver
disegnato
gli
archi
3
2
corrispondenti a cos =
, trovare
dell’arco nel quarto quadrante le altre
funzioni trigonometriche.
2.2. Sapendo che è acuto e positivo e che
sen = 3/5 calcolarne le altre funzioni
trigonometriche.
3.3. Ragionando solo sulla circonferenza
goniometrica completare con i segni > = <
le seguenti:
sen
6
...........sen
6
sen
4
cos
sen
cos
6
6
6
........... cos
sen
cos
3
3
6
cos
4
...........0
...........0
4.4. Ragionando solo sulla circonferenza
goniometrica provare che:
sen– ) = sen
sen (–) = cos
sen ( ) = - sen
sen- sen
5.5. Semplificare le seguenti espressioni:
tg)sen(-) cos( + ) + tg2(-)cos2()=
[0]
sen4 – sen2 – cos4 + cos2
Esistono utili formule per il calcolo delle
funzioni trigonometriche, che sono riportate in
fondo.
VARIAZIONE DELLE FUNZIONI TRIGONOMETRICHE:
Ricordando la definizione data osserviamo che:
- 1 sen 1; - 1 cos 1
I grafici delle funzioni trigonometriche sono i seguenti:
y = sen x
definita per ogni x, il codominio è [-1,1], periodica di periodo 2interseca l’asse x nei punti della
forma k , con k Z.
y = cos x
definita per ogni x, il codominio è [-1,1], periodica di periodo 2 , interseca l’asse x nei punti della
k
forma 2
, con k Z.
y = tg x
definita per x /2 + kil codominio è R periodica di periodo interseca l’asse x nei punti della
forma k , con k Z.
Esercizi
Prova a disegnare i grafici di:
1. 1. sin 2 x
2. 2. 3 cos x
RISOLUZIONE DELLE EQUAZIONI
PRIMO GRADO, elementari
1. 1. sinx = h
2.
. cosx = h
con h [-1, 1]
2
Ricordando la definizione delle funzioni sinx e cosx queste equazioni si risolvono intersecando la
2
2
circonferenza (di equazione x y 1 ) con l’equazione
1. 1. y = h
2. 2. x = h
(che rappresenta una retta)
Esempio:
sen x = ½
x 2 y 2 1
Può essere interpretata come : y 1 / 2
disegnando la circonferenza goniometrica e la retta y = 1/2 si ha:
I punti di intersezione sono posizionati nel primo quadrantex = /6,
e nel secondo, x /6 = 5/6
In questo modo abbiamo trovato le due soluzioni, ma ricordando che la funzione seno è periodica di
periodo 2 se voglio ottenere tutte le soluzioni dell’equazione ho:
x = /6 + 2k,
x = 5/6 + 2k, con k Z
cos x = -1/2
disegnando la circonferenza goniometrica e la retta x = -1/2 si ha:
In questo caso i punti di intersezione sono posti nel secondo e terzo quadrante.
L’arco con cos x = + ½ è x /3,
quindi quello posto nel secondo quadrante sarà
x = – /3 = 2/3
mentre quello nel terzo quadrante sarà.
x = + /3 = 4/3
Le soluzioni sono quindi, tenendo conte del periodo:
x = 2/3 k
x = 4/3 kcon k Z
PRIMO GRADO, lineari
3. 3. asenx + bcosx
=h
2
2
Si risolvono intersecando la circonferenza (di equazione x y 1 ) con l’equazione
ay + bx =h(che rappresenta una retta)
Esempio
senx + cos x =1
Si pone y = senx, x= cosx e si interseca la retta y = -x + 1 così ottenuta con la circonferenza di
equazione x 2 + y2 =1
Si ottengono i punti (0,1) e (1,0) che corrispondono alle soluzioni x = 0, x /2
considerando poi il periodo si ha:x = 0 + 2k, x /2 + 2kcon k Z.
SECONDO GRADO
1. 1. Se l’equazione data contiene una sola funzione trigonometrica si risolve mediante la
b b 2 4ac
2a
formula generale delle equazioni di secondo grado, ossia
.
2. 2. Se contiene più di una funzione si cerca, mediante le formule viste precedentemente, di
trasformarla in una che contenga una sola funzione trigonometrica.
x1, 2
Esempio
2 cos 2 x cos x 1 0
Applicando la formula risolutiva si ha:
cos x1, 2
1 1 8
1;1 / 2
4
ora risolvo le equazioni cos x = ½,
x = /3 k
cos x = -1
x = k
x = -/3 kcon k Z.
Risolviamo ora:
cos2x – sen2x + cos x = 0
è di secondo grado, ed in essa non compare una sola funzione goniometrica; ricordando che
sen2x = 1 – cos2x si ha:
cos2x –1 + cos2x + cos x = 0
2 cos2x + cos x – 1 = 0
da cui si ottiene l’equazione precedente .
Esercizi
1. Risolvere le seguenti equazioni:
sen (2x –/2) = ½
2cos2x – cos x – 1= 0
cos x = sen2x – cos2x
sen /4 + x) + sen /4 –x) = 1
sen x = sen 2x
2 cos x + 2 sen x = 3 +1
[x = /3 +2k, x=2/3 + 2k]
[ x = 2k, x = 2/3 + 2k]
[x = + 2k, x = /3 + 2k]
[x = /4 + 2k]
[x = k, x = /3 + 2k]
[x =/6 + 2k, x = /3 + 2k]
RISOLUZIONE DI DISEQUAZIONI TRIGONOMETRICHE
Disequazioni elementari
Consideriamo ad esempio la disequazione sen x > ½
Disegnando la circonferenza e la retta y = ½ cerco tutti gli archi per cui l’ordinata è maggiore di ½,
ed ottengo la soluzione
/6 + 2kx 5/6 + 2k, con k Z.
quindi ricordando che - 1 sen 1;
- 1 cos 1
Disequazione: sen x a
a 1:
a 1 :
a 1 :
1 a 1:
impossibile
sempre vera
3
x 2k
2
vera
1 2k x 2 2k , con k Z
Disequazione sen x a
a 1:
impossibile
a 1:
sempre vera
x 2k
a 1:
2
vera
1 a 1 : 2 2k x 2 2 2k , con k Z
Disequazione cos x a
a 1:
impossibile
a 1 :
sempre vera
a 1 :
vera x 2k
1 a 1 : 2k x 2k , con arccos a , k Z
Disequazione cos x a
a 1:
sempre vera
a 1 :
impossibile
a 1 :
vera x 2k
1 a 1:
2k x 2 2k , con k Z
Disequazioni lineari
Nel caso di una disequazione lineare del tipo asenx + bcosx > (<) h si procede come per l’equazione
2
2
corrispondente, cioè si risolve intersecando la circonferenza di equazione x y 1 con la
disequazione ay + bx >h (che rappresenta un semipiano)
Esempio
senx + cos x <1
Si pone y = senx, x= cosx e si interseca il sempipiano y < -x + 1 così ottenuto con la circonferenza
di equazione x 2 + y2 =1
Si ottiene così la soluzione: /2+ 2k x <2 + 2kcon k Z
Disequazioni di 2 grado
Si risolvono come le disequazioni di secondo grado, scegliendo gli intervalli interni o esterni alle
soluzioni trovate, si ottengono così delle disequazioni di primo grado che si risolvono come
precedentemente visto.
Esempio
2sen2x –sen x –1 >0
risolvendo l’equazione 2sen2x –sen x –1 =0 ottengo, mediante la formula risolutiva delle equazioni
di secondo grado: sen x = 1 sen x = -1/2, da cui, prendendo i valori esterni si ha:
sen x > 1 sen x < -1/2
cioè:
sen x >1 non dà soluzioni, mentre sen x < ½ ha come soluzioni 7/6 + 2k < x < 11/6 + 2kcon
k Z
Esercizi
1.
1.
Risolvere le seguenti disequazioni:
cos x > ½
[-/3 + 2k< x < /3 + 2k]
2 cos2x – cos x < 0
[/3 + 2k< x < /2 + 2k
3/2 + 2k< x < 5/3 + 2k]
[/6 + 2k< x < 5/6 + 2k
+ 2k< x < 2 + 2k]
sen x + cos 2x < 1
cos x -
3 sen x > 0
3 sen x + cos x > 1
2 cos x 3
0
senx
[-5/6 + 2k< x < /6 + 2k]
[ 2k< x < 2/3 + 2k]
[ + 2k< x < 2 + 2k]
FORMULE DI TRIGONOMETRIA
Formule di addizione e sottrazione:
sen( + ) = sencos + cossen
sen( - ) = sencos - cossen
cos( + ) = coscos - sensen
cos( - ) = coscos + sensen
tg tg
tg( )
1 tgtg
tg tg
tg( )
1 tgtg
Formule di duplicazione:
(si ottengono dalle precedenti ponendo =)
sen 2 = 2sencos
cos 2 = cos2 - sen2 = 1 – 2sen2 = 2cos2 -1
2tg
tg 2
1 tg 2
Formule di bisezione:
(si ottengono dalle precedenti dimezzando l’angolo )
sin
2
1 cos
2
1 cos
2
2
1 cos 1 cos
sin
tg
2
1 cos
sin
1 cos
cos
Formule parametriche:
tan
(ESPRESSIONI DI sen, cos IN FUNZIONE RAZIONALE DI t =
2t
1 t2
1 t2
cos
1 t2
2t
tg
1 t2
sin
2)
Formule di prostaferesi:
pq
pq
cos
2
2
pq
pq
sin p sin q 2 cos
sin
2
2
pq
pq
cos p cos q 2 cos
cos
2
2
pq
pq
cos p cos q 2 sin
sin
2
2
sin p sin q 2 sin
Formule di Werner:
1
cos( ) cos( )
2
1
cos cos cos( ) cos( )
2
1
sin cos sin( ) sin( )
2
sin sin
Appendice 1
Funzioni goniometriche inverse
Considerata la funzione y=senx è possibile invertirla, sotto opportune condizioni, e si ottiene la
funzione :
y=arcsen x
definita per -1 x 1 , a valori in –/2 f(x) /2
nello stesso modo se operiamo con la y = cos x otteniamo la
y = arccos x
definita per -1 x 1 , a valori in 0 f(x)
e con y = tg x si ha:
y = arctg x
definita per ogni x , a valori in –/2 f(x) /2
Appendice 2
Relazioni tra gli elementi di un triangolo rettangolo
b = a sen
b = a cos
c = a sen
c = a cos
b = c tg
b = c cotg
c = b tg
c = b cotg
Relazioni tra gli elementi di un triangolo qualsiasi
I due seguenti teoremi si utilizzano quando di un triangolo qualsiasi devo determinare lati e angoli
a
b
c
Teorema dei seni: sen sen sen si utilizza se sono noti due lati e un angolo ad essi
opposto, oppure un lato e due angoli qualunque
Esempio
30 0 , 45 0 , a 16
40 0 , b 15, a 25
sin 30 sin 45
2 1
b 16
22.62
16
b
2 2
sin 40 sin
sin 0.38
25
15
Teorema del coseno: a2 = b2 + c2 – 2bc cos si utilizza quando del triangolo sono noti due lati e
l’angolo tra essi compreso oppure tre lati.
Esempio
60 0 , a 5, b 8 c 2 a 2 b 2 2ab cos 60 0 25 64 2 5 8
1
49
2
per cui
c 7, a 5, b 6 cos 0.2, 1.37
0
(radianti: 78.7 )
FORMULARIO DI ALGEBRA
Valore assoluto (modulo)
x0
x , se
x
x0
x , se
1.a m a n a m n
2.a m : a n a m n , a 0
n
3. a m
a m n
4.a b a m b m
m
n
an
a
5. n , b 0
b
b
m
Proprietà delle potenze
6. a n n a m
a a 0
m
n
1
(N.B.: a 1; a a )
1
a 0
an
1
( a 0)
n
am
a n
a
m
n
Potenza con esponente negativo
Prodotti notevoli
se n pari e m dispari, a>0
a b 2 a 2 2ab b 2
a b 2 a 2 2ab b 2
a b c 2 a 2 b 2 c 2 2ab 2ac 2bc
a b 3 a 3 3a 2 b 3ab 2 b 3
a b 3 a 3 3a 2 b 3ab 2 b 3
a 2 b 2 a b a b
a b a
a 3 b 3 a b a 2 ab b 2
a b
3
Scomposizione in fattori
Radicali
3
ab b
2
x 2 x1 x 2 x x1 x2 x x1 x x 2
m
ab m a m b
m
a : b m a : m b , b 0
m
n
a n am
1
Razionalizzazione
2
a
a a 0
n
a
a 0
a
m
se m pari, a e b0
Equazioni
Primo grado
ax b 0
x
se a 0,
se a 0 e b 0 ,
se a 0 e b 0 ,
Secondo grado
b
a
impossibile
indeterminata
ax 2 bx c 0
b b 2 4ac
2a
a 0,
x1, 2
b 0,
ax 2 c 0, x1, 2
c 0,
x1 0
ax bx 0,
b
x 2 a
se
se
se
c
a
2
2
se b 4ac 0 ,
impossibile in R
ax 4 bx 2 c 0,
Biquadratica
Proprietà dei logaritmi
x 2 z az 2 bz c 0
1. log a (b c) log a b log a c (b, c 0 , a 1)
b
log a log a b log a c
(b, c 0 , a 1)
c
2.
c
3. log a b c log a b
altre relazioni importanti
log a 1 0
(a 1)
log a a 1
(a 1 a)
log a b
cambiamento di base nei logaritmi
log c b
log c a
(b 0 , a 1)
(a, b, c, 0)