vol1_blu_rec_17 1..9

Scheda
17
Scheda per il recupero 17
A Ripasso
Rette perpendicolari e rette parallele
Rette perpendicolari e parallele
DOMANDE
RISPOSTE
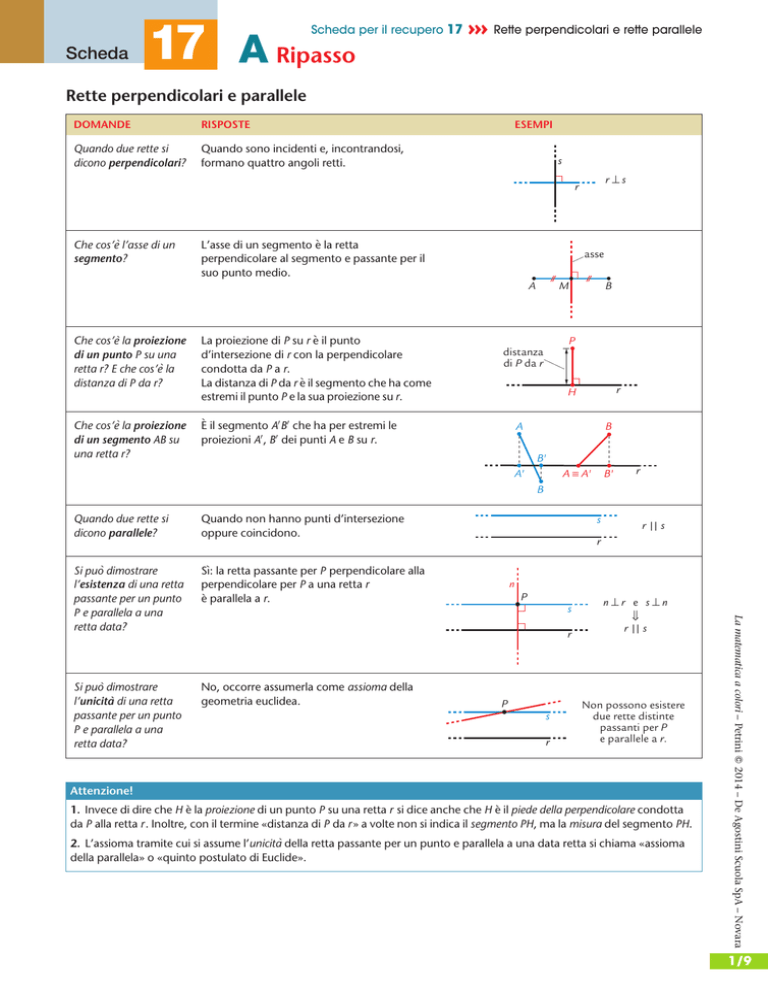
Quando due rette si
dicono perpendicolari?
Quando sono incidenti e, incontrandosi,
formano quattro angoli retti.
ESEMPI
s
r⊥s
r
Che cos’è l’asse di un
segmento?
L’asse di un segmento è la retta
perpendicolare al segmento e passante per il
suo punto medio.
asse
A
Che cos’è la proiezione
di un punto P su una
retta r? E che cos’è la
distanza di P da r?
La proiezione di P su r è il punto
d’intersezione di r con la perpendicolare
condotta da P a r.
La distanza di P da r è il segmento che ha come
estremi il punto P e la sua proiezione su r.
Che cos’è la proiezione
di un segmento AB su
una retta r?
È il segmento A0 B 0 che ha per estremi le
proiezioni A0 , B 0 dei punti A e B su r.
M
B
P
distanza
di P da r
r
H
A
B
B'
A ≡ A'
A'
B'
r
B
Quando non hanno punti d’intersezione
oppure coincidono.
Si può dimostrare
l’esistenza di una retta
passante per un punto
P e parallela a una
retta data?
Sı̀: la retta passante per P perpendicolare alla
perpendicolare per P a una retta r
è parallela a r.
Si può dimostrare
l’unicità di una retta
passante per un punto
P e parallela a una
retta data?
No, occorre assumerla come assioma della
geometria euclidea.
s
r || s
r
n
P
s
r
P
s
r
n⊥r e s⊥n
⇓
r || s
Non possono esistere
due rette distinte
passanti per P
e parallele a r.
Attenzione!
1. Invece di dire che H è la proiezione di un punto P su una retta r si dice anche che H è il piede della perpendicolare condotta
da P alla retta r . Inoltre, con il termine «distanza di P da r » a volte non si indica il segmento PH, ma la misura del segmento PH.
2. L’assioma tramite cui si assume l’unicità della retta passante per un punto e parallela a una data retta si chiama «assioma
della parallela» o «quinto postulato di Euclide».
La matematica a colori – Petrini f 2014 – De Agostini Scuola SpA – Novara
Quando due rette si
dicono parallele?
1/9
Scheda
17
Scheda per il recupero 17
Rette perpendicolari e rette parallele
A Ripasso
Criterio di parallelismo
Due rette tagliate da una trasversale sono parallele se e solo se formano una coppia di angoli:
alterni interni congruenti
oppure
oppure
alterni esterni congruenti
coniugati interni supplementari
oppure
oppure corrispondenti congruenti
coniugati esterni supplementari
Proprietà degli angoli nei poligoni
TEOREMA
A PAROLE
Angoli esterni di un
triangolo
L’ampiezza di ciascun angolo esterno di un
triangolo è la somma delle ampiezze degli
angoli interni non adiacenti.
Somma degli angoli
interni di un
triangolo
La somma delle ampiezze degli angoli interni
di un triangolo è sempre uguale a 180 .
Angoli acuti di un
triangolo rettangolo
Gli angoli acuti di un triangolo rettangolo
sono complementari.
ESEMPI
β
γ=α+β
γ
α
β
α + β + γ = 180°
α
γ
β
β + γ = 90°
Somma degli angoli
interni di un
poligono
La somma delle ampiezze degli angoli interni
di un poligono di n lati è uguale a
ðn 2Þ180 .
α
n = 4, quindi
α +β + γ + δ =
= (4 – 2) · 180° = 360°
δ
γ
Somma degli angoli
esterni di un
poligono
La somma delle ampiezze degli angoli esterni
di un poligono (uno per ciascun lato) è
sempre 360 , indipendentemente dal
numero dei lati del poligono.
β
α
α + β + γ + δ = 360°
δ
γ
β
La matematica a colori – Petrini f 2014 – De Agostini Scuola SpA – Novara
γ
2/9
Scheda
17
Scheda per il recupero 17
Rette perpendicolari e rette parallele
A Ripasso
Altri criteri di congruenza
TEOREMA
A PAROLE
Secondo criterio
generalizzato
Due triangoli aventi un lato e
due angoli ordinatamente
congruenti sono congruenti.
IN SIMBOLI
A
A'
B
C
B'
C'
BC ffi B C , Bb ffi Bb0 , Ab ffi Ab0 ) ABC ffi A B C 0
0
Criterio di
congruenza per i
triangoli rettangoli
0
Due triangoli rettangoli sono
congruenti se hanno
congruenti, rispettivamente,
un cateto e l’ipotenusa.
0 0
C
A
B
C'
A'
B'
) ABC ffi A0 B 0 C 0
AC ffi A0 C 0 , BC ffi B0 C 0 , Bb ffi Bb0 ffi
2
Attenzione!
Nel secondo criterio generalizzato, è essenziale l’avverbio «ordinatamente»: è essenziale, cioè, che il lato congruente sia
opposto, nei due triangoli, a due angoli congruenti.
Scheda
a.
b.
c.
d.
e.
B Verifica delle conoscenze
Vero o falso?
sia r una retta; se P 2 r allora esistono infinite rette per P perpendicolari a r
se r ? s e s ? t, allora anche r ? t
le bisettrici di due angoli supplementari sono perpendicolari
se ABC è un triangolo isoscele, sulla base BC, allora A appartiene all’asse di BC
sia H la proiezione di P su una retta r e Q un punto di r diverso da H, allora PQ > PH
V
F
V
F
V
F
V
F
V
F
[3 affermazioni vere e 2 false]
2
a.
b.
c.
d.
3
a.
b.
c.
d.
e.
f.
Fai riferimento alla figura qui a fianco e rispondi alle seguenti domande.
D
Quali degli angoli 1, 2, 3 e 4 sono congruenti, se AB k DC?
Quali degli angoli 1, 2, 3 e 4 sono congruenti, se AD k BC?
bB, se AB k DC?
Quale angolo è supplementare a DA
bC, se AD k BC?
Quale angolo è supplementare ad AD
C
2 3
1 4
A
B
Completa, facendo riferimento alla figura qui a fianco:
se 1
se 2
se 3
se 3
se 4
se 6
ffi 2 , allora sono parallele le due rette ...............;
ffi 5 , allora sono parallele le due rette ...............;
e 4 sono supplementari, allora sono parallele le due rette ...............;
ffi 6 , allora sono parallele le due rette ....................;
e 7 sono supplementari, allora sono parallele le due rette ...............;
ffi 7 , allora sono parallele le due rette ............... .
a
α1
b
α3
α2 α4
α5
c
α6
α7
d
e
La matematica a colori – Petrini f 2014 – De Agostini Scuola SpA – Novara
1
17
3/9
Scheda
17
Scheda per il recupero 17
Rette perpendicolari e rette parallele
B Verifica delle conoscenze
4
Quanti angoli ottusi può avere al massimo un triangolo? :::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::
5
La somma delle ampiezze degli angoli interni di un quadrilatero è :::::::::::::::::::::::::::::: .
6 La somma delle ampiezze degli angoli interni di un poligono dipende dal numero dei lati del poligono? ::::::::::::::: E la
somma delle ampiezze degli angoli esterni ? :::::::::::::::
Qual è l’ampiezza di ciascuno degli angoli interni di un triangolo equilatero?
angoli esterni? ::::::::::::::::::::
7
8 Qual è la somma delle ampiezze degli angoli interni di un ottagono?
angoli esterni di un ottagono? ::::::::::::::::::::
::::::::::::::::::::
:::::::::::::::
E l’ampiezza di ciascuno degli
Qual è la somma delle ampiezze degli
Test
Quale delle seguenti proprietà non si può dimostrare e abbiamo dovuto assumere come assioma?
9
A
l’esistenza della retta passante per un punto e perpendicolare a una retta assegnata
B
l’unicità della retta passante per un punto e perpendicolare a una retta assegnata
C
l’esistenza della retta passante per un punto e parallela a una retta assegnata
D
l’unicità della retta passante per un punto e parallela a una retta assegnata
10 In riferimento alla figura qui a fianco, quale affermazione è corretta?
A
1 e 2 sono alterni interni
B
1 e 2 sono alterni esterni
C
3 e 2 sono corrispondenti
D
nessuna delle precedenti affermazioni è esatta
a
α1
α3
b
α2
α4
c
11 Quale delle seguenti non è una condizione necessaria e sufficiente perché due rette, tagliate da una trasversale, siano parallele?
A
Avere due angoli alterni interni congruenti
B
Avere due angoli alterni esterni congruenti
C
Avere due angoli corrispondenti congruenti
D
Avere due angoli coniugati interni congruenti
A
Sı̀, in base al primo criterio di congruenza
B
Sı̀, in base al secondo criterio di congruenza generalizzato
C
Sı̀, in base al terzo criterio di congruenza
D
Non possiamo affermare che i due triangoli sono congruenti
A
B
b?
b è 15 e l’ampiezza di Bb è 35 . Qual è l’ampiezza di C
13 In un triangolo ABC, l’ampiezza di A
A
110
B
120
C
130
D
A'
C
B'
C'
Nessuna delle precedenti
14 In un triangolo ABC, isoscele sulla base AB, l’ampiezza dell’angolo al vertice è 20 . Qual è l’ampiezza di ciascuno de-
gli angoli adiacenti ad AB?
A
70
B
80
C
90
D
100
15 In quale dei seguenti poligoni la somma delle ampiezze degli angoli esterni è 200 ?
A
In un decagono
B
In un poligono di 20 lati
C
In ogni poligono
D
In nessun poligono
16 In un poligono la somma degli angoli interni è 1620 ; quanti lati ha il poligono?
A
9
B
10
C
11
D
12
La matematica a colori – Petrini f 2014 – De Agostini Scuola SpA – Novara
12 Nei triangoli disegnati nella figura qui sotto a destra, gli angoli contrassegnati con lo stesso simbolo sono congruenti. Possiamo dire che i due triangoli sono congruenti?
4/9
Scheda
17
Scheda per il recupero 17
Rette perpendicolari e rette parallele
C Esercizi guidati
Negli esercizi 1-2-3, fai riferimento al teorema che ha come modello la figura sotto e come ipotesi
e tesi quelle specificate.
C
IPOTESI:
ABC è un triangolo acutangolo, CH ffi CK, AH?BC e BK?AC
TESI:
ABC è isoscele sulla base AB
K
H
B
A
Completa l’enunciato del teorema: «Sia ABC un triangolo acutangolo e siano AH e BK le ::::::::::::::::::::::::: relative ai lati
:::::::::::::::::::::::::::::: . Dimostra che, se il triangolo KHC è :::::::::::::::::::: sulla base ::::::::::, allora ABC è ::::::::::::::::::::::::::::::::::::::::::::: ».
1
2
Completa e indica con una crocetta le risposte esatte.
a. In base alle ipotesi si può affermare che i triangoli AHC e BKC hanno:
due lati e l’angolo compreso ordinatamente congruenti
un lato e gli angoli adiacenti ordinatamente congruenti
i tre lati ordinatamente congruenti
nessuna delle precedenti risposte è corretta
C
b. Di conseguenza si può affermare che AHC e BKC sono:
congruenti per il primo criterio
congruenti per il secondo criterio
congruenti per il terzo criterio
nessuna delle precedenti risposte è corretta
K
c. Come conseguenza di quanto dimostrato nel punto precedente si può affermare che:
AC ffi BC, quindi ABC è isoscele
bB ffi CBbA, quindi ABC è isoscele
CA
nessuna delle precedenti risposte è corretta
H
A
B
3 Scrivi in forma discorsiva la dimostrazione del teorema espresso nell’esercizio 1 seguendo i passi suggeriti nell’esercizio precedente.
a. Indica nella figura con l’ampiezza degli angoli alla base del triangolo ABC e con l’ampiezza degli angoli alla base del triangolo isoscele ACD.
b. Quanto vale, in funzione di e , la somma delle ampiezze degli angoli del triangolo ABD?
þ
2 þ þ 2
2 þ 2
c. In base al teorema sulla somma delle ampiezze degli angoli interni di un triangolo, a che cosa deve essere uguale 2 þ 2? .............................. Che cosa puoi dedurre a proposito di þ ? ...............
bD?
d. Tenendo conto di quanto ricavato nei punti precedenti, che cosa puoi dedurre dell’angolo BA
Che è retto
Che è acuto
bD dipende da e Che l’ampiezza di BA
D
C
A
B
Negli esercizi 5-6-7, fai riferimento al teorema che ha come modello la seguente figura e come ipotesi e tesi
quelle indicate qui di seguito.
B
B'
P
A
C
A'
bP ffi P A
bC e B0 Ab0 P0 ffi P 0 Ab0 C0
b ffi Ab0 , Bb ffi Bb0 ffi , AP ffi A0 P 0 , BA
IPOTESI: A
2
TESI:
ABC ffi A0 B0 C0
P'
C'
La matematica a colori – Petrini f 2014 – De Agostini Scuola SpA – Novara
4 Considera la figura sotto: ABC è un triangolo isoscele sulla base AB e il lato obliquo BC è stato prolungato di un segmento CD, congruente a BC.
5/9
Scheda
17
Scheda per il recupero 17
C Esercizi guidati
Rette perpendicolari e rette parallele
Completa l’enunciato del teorema che ha le ipotesi e la tesi indicate nella pagina precedente: «due triangoli rettangoli
sono .............................. se hanno congruenti, ordinatamente un angolo .............................. e .......................................................».
5
6
Completa le parti mancanti e indica con una crocetta le risposte corrette.
a. I due triangoli ABP e A0 B0 P 0 sono congruenti. Per quale ragione?
Per il primo criterio di congruenza
Per il secondo criterio di congruenza
Per il secondo criterio di congruenza generalizzato
Per il criterio di congruenza dei triangoli rettangoli
b. Si può affermare che AB ffi :::::::::: Per quale ragione?
Per ipotesi
Perché elementi corrispondenti nei triangoli congruenti ............... e ...............
Perché opposti ad angoli congruenti per ipotesi
Perché opposti ai segmenti AP e A0 P 0 , congruenti per ipotesi
c. I due triangoli ABC e A0 B0 C0 sono congruenti:
Per il primo criterio di congruenza
Per il secondo criterio di congruenza
Per il secondo criterio di congruenza generalizzato
Per il criterio di congruenza dei triangoli rettangoli
7 Scrivi in forma discorsiva la dimostrazione del teorema espresso nell’esercizio 5, seguendo i passi suggeriti nell’esercizio precedente.
8
Completa la seguente tabella in cui ti guidiamo a svolgere una dimostrazione.
Passi
Dato un triangolo ABC, isoscele sulla base AB, traccia da A la retta perpendicolare ad AC che
incontra il prolungamento di BC nel punto E e da B la retta perpendicolare a BC, che incontra
il prolungamento di AC nel punto D.
Dimostra che AD ffi BE.
Figura
C
D
Ipotesi
:::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::
Tesi
:::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::
Dimostrazione
I triangoli BCD e ACE hanno:
b in comune;
l’angolo C
B
E
CBbD ffi :::::::::: perché :::::::::::::::;
CB ffi :::::::::: perché ABC è un triangolo ::::::::::::::: .
Pertanto i triangoli considerati sono congruenti in base al ::::::::::::::: criterio di congruenza.
In particolare DC ffi :::::::::::::::, quindi AD ffi BE in quanto differenze di
:::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::: .
La matematica a colori – Petrini f 2014 – De Agostini Scuola SpA – Novara
A
6/9
Scheda
9
17
Scheda per il recupero 17
Rette perpendicolari e rette parallele
C Esercizi guidati
Completa la seguente tabella in cui ti guidiamo a svolgere una dimostrazione.
Passi
Due rette parallele a e b, sono tagliate da una trasversale c, che interseca la retta a in A e la
retta b in B.
Considera due punti C 2 a, D 2 b, appartenenti allo stesso semipiano avente come origine la
retta c, tali che AC ffi BD e dimostra che AB k CD.
Figura
c
A
a
C
b
B
D
Ipotesi
:::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::
Tesi
:::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::
Dimostrazione
I due triangoli ABD e ACD hanno:
AD
in comune
AC ffi BD
bC ffi :::::::::::::::
DA
per :::::::::::::::::::::::::
perché angoli
trasversale AD
::::::::::::::::::::
rispetto alle parallele a e b tagliate dalla
Pertanto ABD e ACD sono congruenti in base al ::::::::::::::::::::::::::::::.
bD ffi :::::::::::::::.
Ne segue in particolare che BA
Ciò significa che le rette AB e CD, tagliate dalla trasversale AD formano angoli
::::::::::::::::::::::::: congruenti, quindi ::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::: .
10 Completa la seguente tabella in cui ti guidiamo a svolgere una dimostrazione.
Passi
Figura
C
A
B
P
Ipotesi
:::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::
Tesi
:::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::
Dimostrazione
I due triangoli rettangoli PAC e ::::::::::::::::::::::::: hanno:
PC
:::::::::::::::::::::::::
AC ffi :::::::::::::::
quindi sono congruenti in base al :::::::::::::::::::::::::::::: .
Ne segue in particolare che ::::::::::::::::::::::::::::::, da cui la tesi.
La matematica a colori – Petrini f 2014 – De Agostini Scuola SpA – Novara
Dato un triangolo ABC, isoscele sulla base AB, conduci da A la perpendicolare ad AC e da B la
perpendicolare a BC. Indica con P il punto d’intersezione delle due perpendicolari. Dimostra
bB.
che la semiretta CP è la bisettrice dell’angolo AC
7/9
Scheda
17
Scheda per il recupero 17
D Esercizi da svolgere
Rette perpendicolari e rette parallele
1
Qual è l’ampiezza degli angoli interni di un poligono di 20 lati, avente tutti gli angoli congruenti?
2
a. Qual è l’ampiezza degli angoli interni di un triangolo rettangolo isoscele?
b. Sia ABC un triangolo rettangolo isoscele di ipotenusa BC. Sia P un punto di BC tale che AB ffi BP. Qual è l’ampiezza
bC?
dell’angolo P A
bB hanno l’ampiezza indicata.
bC e AC
3 Nella figura qui sotto BC ffi BD e gli angoli BA
C
76°
38°
A
B
D
a. In base al teorema dell’angolo esterno, qual è l’ampiezza di CBbD?
bB.
b. Deduci qual è l’ampiezza di CD
4 Stabilisci se esiste un poligono che soddisfa ciascuna delle seguenti condizioni. Se esiste un tale poligono, stabilisci
quanti lati deve avere:
a.
b.
c.
d.
e.
f.
un poligono tale che la somma delle ampiezze degli angoli interni sia 1080 ;
un poligono tale che la somma delle ampiezze degli angoli interni sia 1000 ;
un poligono tale che la somma delle ampiezze degli angoli esterni sia 500 ;
un poligono tale che la somma delle ampiezze degli angoli esterni sia 360 ;
un poligono i cui angoli interni hanno tutti ampiezza uguale a 144 ;
un poligono i cui angoli interni hanno tutti ampiezza uguale a 120 .
5 Scrivi l’enunciato del teorema che ha come modello la seguente figura e l’ipotesi e la tesi indicate di seguito. Poi dimostra il teorema.
C
IPOTESI:
TESI:
DE ffi EF e CE ffi EB
AC k BF
E
F
D
A
B
6 Scrivi l’enunciato del teorema che ha come modello la seguente figura e l’ipotesi e la tesi indicate di seguito. Poi dimostra il teorema.
C
bD ffi DA
bB e EG k AD
IPOTESI:
CA
G
AF ffi AE
F
E
A
D
B
7 Due segmenti AB e CD hanno entrambi come asse la retta r. I punti A e C appartengono al semipiano, avente come
origine r, opposto a quello a cui appartengono B e D. Inoltre A, B, C e D non sono allineati.
Disegna due segmenti AB e CD che soddisfino tali condizioni e dimostra che AC ffi BD.
8 Siano a e b due rette parallele. Considera un punto A 2 a, un punto B 2 b e conduci per un punto P del segmento
AB una retta che interseca a in C e b in D. Dimostra che i triangoli APC e BPD hanno gli angoli congruenti.
9 Sia ABC un triangolo. Sulla parallela alla retta BC passante per A considera un punto D, appartenente allo stesso semipiano avente come origine la retta AB a cui appartiene il triangolo, tale che AD ffi BC. Dimostra che i due triangoli
ABC e ADC sono congruenti.
10 Due triangoli ABC e ABD appartengono a semipiani opposti aventi come origine la retta AB e sono tali che
AC ffi BD e BC ffi AD. Dimostra che AC k BD.
11 Sia ABC un triangolo isoscele sulla base AB. Conduci una parallela ad AB che interseca AC in D e BC in E. Considera
su AB il punto F tale che AF ffi DE e dimostra che AD k EF. Conduci poi da B la parallela a EF che incontra in G il prolungamento di DE e dimostra che AD ffi EB ffi EF ffi BG.
La matematica a colori – Petrini f 2014 – De Agostini Scuola SpA – Novara
TESI:
8/9
Scheda
17
Scheda per il recupero 17
D Esercizi da svolgere
Rette perpendicolari e rette parallele
12 Dato un triangolo ABC, rettangolo in A, considera un punto D sul prolungamento di BC, dalla parte di C. Dal punto
D conduci la perpendicolare a BD e indica con E il punto in cui incontra il prolungamento di AC, dalla parte di C. Dimostra che ABbC ffi CEbD.
b di un triangolo ABC. Dimostra che l’angolo BPbC
beC
13 Sia P il punto d’intersezione delle due bisettrici degli angoli B
non può essere retto.
14 In un triangolo ABC, traccia le altezze AK e BH. Dimostra che, se AH ffi BK, allora ABC è isoscele sulla base AB.
15 Sia ABC un triangolo rettangolo, di ipotenusa BC. Conduci la bisettrice CP e indica con H la proiezione di P su BC.
Dimostra che il triangolo ACH è isoscele sulla base AH.
16 Dimostra che le altezze relative ai lati obliqui di un triangolo isoscele sono congruenti.
17 Dimostra che due triangoli rettangoli sono congruenti se hanno ordinatamente congruenti l’altezza relativa all’ipotenusa e un angolo acuto.
18 In un triangolo ABC, traccia la mediana BM. Siano H e K, rispettivamente, le proiezioni di A e C sulla retta BM. Dimostra che AH ffi CK e AK ffi CH.
19 Sia ABC un triangolo. Traccia da C la mediana CM e indica con H e K, rispettivamente, le proiezioni di A e B sulla
retta CM. Dimostra che:
a. AH ffi BK e AK ffi BH;
b. AK k BH.
20 Dato il triangolo ABC, prolunga il lato AB, dalla parte di A, di un segmento AD ffi AB e il lato AC, sempre dalla parte
di A, di un segmento AE ffi AC. Dimostra che i segmenti BE e DC sono congruenti e paralleli.
b e Bb del triangolo ABC. Dimostra che l’angolo APbB è ottuso.
21 Sia P il punto d’intersezione delle bisettrici degli angoli A
La matematica a colori – Petrini f 2014 – De Agostini Scuola SpA – Novara
9/9