Trigonometria
Studiare un rapporto tra misure di segmenti
Problema
Sia ABC un triangolo rettangolo in A con l’angolo nel vertice B di 30°. Detta la semicirconferenza di
diametro BC non contenente il vertice A, fissare su un punto P e siano H e K le sue proiezioni ortogonali
rispettivamente sulle rette dei lati AB, AC del triangolo ABC. Considerata la proiezione ortogonale N di P su
BC, determinare per quale posizione di P rapporto tra la somma delle misure dei segmenti PH, PK con la
misura di PN vale
3 1.
Soluzione
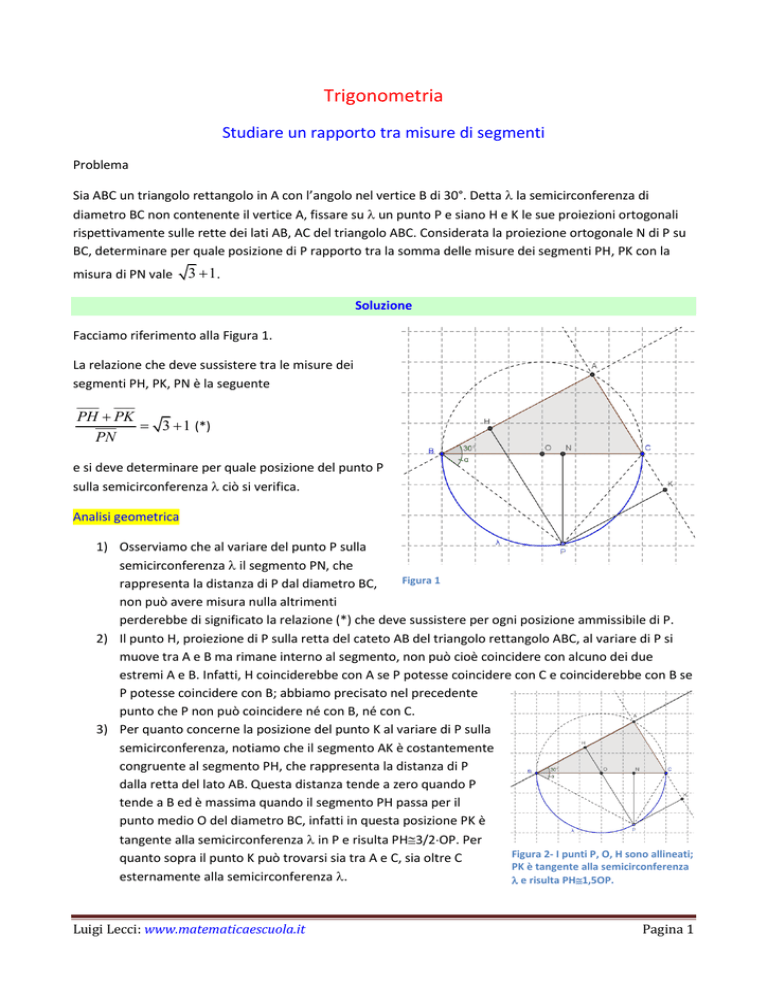
Facciamo riferimento alla Figura 1.
La relazione che deve sussistere tra le misure dei
segmenti PH, PK, PN è la seguente
PH PK
3 1 (*)
PN
e si deve determinare per quale posizione del punto P
sulla semicirconferenza ciò si verifica.
Analisi geometrica
1) Osserviamo che al variare del punto P sulla
semicirconferenza il segmento PN, che
Figura 1
rappresenta la distanza di P dal diametro BC,
non può avere misura nulla altrimenti
perderebbe di significato la relazione (*) che deve sussistere per ogni posizione ammissibile di P.
2) Il punto H, proiezione di P sulla retta del cateto AB del triangolo rettangolo ABC, al variare di P si
muove tra A e B ma rimane interno al segmento, non può cioè coincidere con alcuno dei due
estremi A e B. Infatti, H coinciderebbe con A se P potesse coincidere con C e coinciderebbe con B se
P potesse coincidere con B; abbiamo precisato nel precedente
punto che P non può coincidere né con B, né con C.
3) Per quanto concerne la posizione del punto K al variare di P sulla
semicirconferenza, notiamo che il segmento AK è costantemente
congruente al segmento PH, che rappresenta la distanza di P
dalla retta del lato AB. Questa distanza tende a zero quando P
tende a B ed è massima quando il segmento PH passa per il
punto medio O del diametro BC, infatti in questa posizione PK è
tangente alla semicirconferenza in P e risulta PH3/2OP. Per
Figura 2- I punti P, O, H sono allineati;
quanto sopra il punto K può trovarsi sia tra A e C, sia oltre C
PK è tangente alla semicirconferenza
esternamente alla semicirconferenza .
e risulta PH1,5OP.
Luigi Lecci: www.matematicaescuola.it
Pagina 1
Determinazione delle misure dei segmenti PH, PK, PN
Indichiamo con la misura dell’angolo PBC e con 2r la misure del diametro BC.
1) Il triangolo BPC è rettangolo in P perché inscritto nella semicirconferenza e risulta
BP BC cos 2r cos . L’angolo PBA misura +30° e dal triangolo rettangolo PBH si ricava
PH BPsen 30 2r cos sen 30 .
2) Per la misura di PK determiniamo prima la misura di PC, quindi consideriamo il triangolo PKC. Si sa
che l’angolo ACB misura 60° e che l’angolo BCP è complementare dell’angolo PBC, dunque l’angolo
PCK misura 180°-(60°+90°-)=30°+. Si ha:
PC BCsen 2rsen ( dal triangolo rettangolo BCP);
PK PCsen 30 2rsen sen 30
3) Misura di PN. Dal triangolo rettangolo PNB otteniamo PN BPsen 2r cos sen .
4) La relazione (*) che deve sussistere assume la seguente forma
2r cos sen 30 2rsen sen 30
PH PK
3 1
3 1
2r cos sen
PN
e per quanto premesso nell’analisi geometrica, tenendo conto che nel triangolo BPC l’angolo in P è
retto, l’ampiezza dell’angolo varia nell’intervallo aperto ]0°;90°[.
L’equazione goniometrica si trasforma come segue
cos sen sen 30
3 1 cos sen
cos sen sen30 cos cos30sen
3 1 cos sen , da quale si perviene alla
forma semplificata
3sen2
3 1 cos sen cos 2 0
Poiché per 0°<<90° risulta cos0 si possono dividere i due membri per cos ottenendo
l’equazione equivalente
3tg 2
3 1 tg 1 0
Risolvendo quest’equazione si ha:
tg
3 1
2
3 1 4 3
2 3
Luigi Lecci: www.matematicaescuola.it
3 1
2 3
3 1
2
3 1
2 3
, da cui
3 1
Pagina 2
tg
1
30 oppure tg 1 45 .
3
Concludiamo che il problema ammette due soluzioni, cioè la relazione sussiste per due diverse
posizioni del punto P sulla semicirconferenza .
Luigi Lecci: www.matematicaescuola.it
Pagina 3