Classe III^B 30/05/2015 Quarta verifica Cognome Nome

1)
Classe III^B 30/05/2015
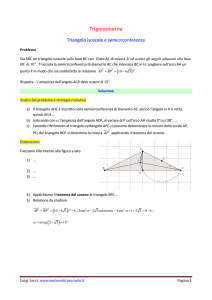
Considera una semicirconferenza di
Quarta verifica
diametro AB, centro O e raggio r. Sul
prolungamento di AB dalla parte di
Cognome Nome---------------------------B, sia C il punto tale che BC=r.
-------------------------------------------------Considera un punto P sulla
semicirconferenza e costruisci il
triangolo rettangolo PCD isoscele sulla base PC, il cui vertice D giace
dalla parte opposta di A rispetto alla retta PC. Determina l’angolo
72 3 2
r
POC in modo che l’area del quadrilatero OCDP sia: 

4


2)
In un triangolo ABC risulta AB=1 e l’angolo ACB=

. Indica con x la
4
misura dell’angolo ABC e con M e N, rispettivamente, i punti medi dei
lati AC e BC.
a. Determina la funzione y  AN
2
2
 BM .
b. Scrivi l’equazione della funzione tramite l’angolo aggiunto e
tracciane il grafico in un intervallo di lunghezza uguale al periodo,
mettendo in evidenza il tratto relativo al problema.
c. Deduci per quale valore di x la somma AN
massimo.
d. Determina per quali valori di x risulta AN
2
2
2
 BM . assume valore
2
 BM 
12  2
8
3)
Data una circonferenza di centro O e raggio r nella quale è inscritto
un triangolo equilatero ABC, si indichino con A’ il punto
diametralmente opposto ad A e con M un punto della
semicirconferenza ABA’(tra B ed A’). Si determini l’area y del
triangolo BCM al variare dell’ampiezza x dell’angolo AOM. Si
rappresenti tale funzione. Si determini poi l’ampiezza dell’angolo
AOM in modo tale che l’area del triangolo BCM sia
Punteggio 1) 9p
3 2
r .
4
2)10p+3p+2p+2p=17p 3)11+2,5p+2,5p=16p