1. Abbiamo - Università degli studi di Bari

SIMULAZIONE I
Cognome e nome …………………………………..
N. di matricola………………….
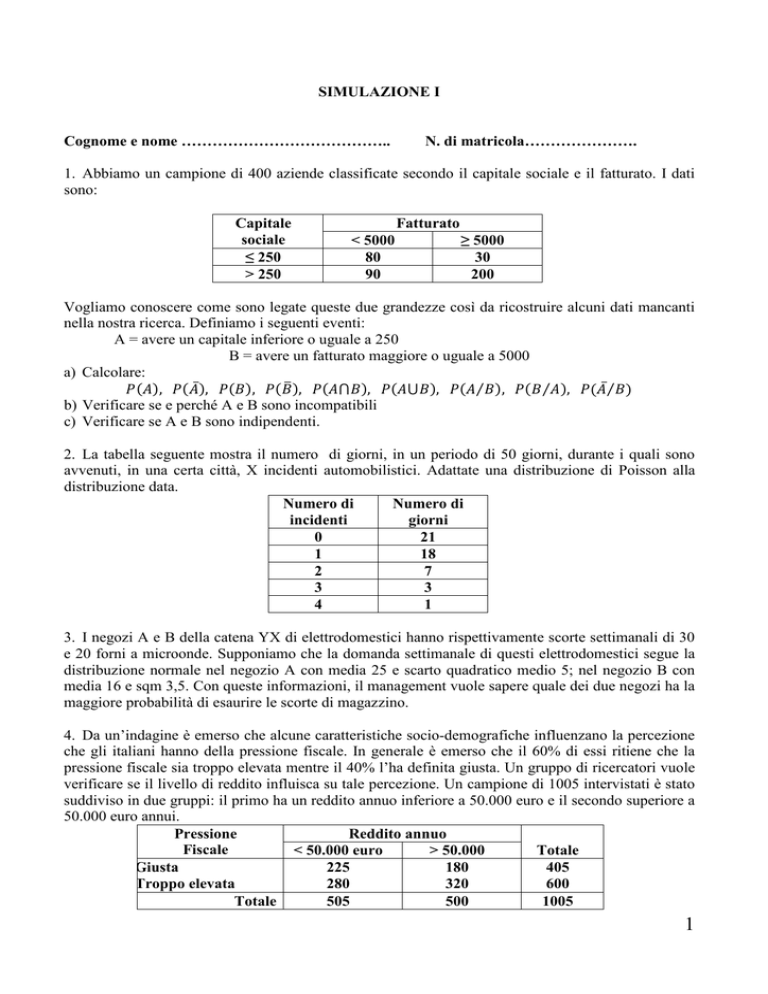
1. Abbiamo un campione di 400 aziende classificate secondo il capitale sociale e il fatturato. I dati
sono:
Capitale
sociale
≤ 250
> 250
Fatturato
< 5000
80
90
≥ 5000
30
200
Vogliamo conoscere come sono legate queste due grandezze così da ricostruire alcuni dati mancanti
nella nostra ricerca. Definiamo i seguenti eventi:
A = avere un capitale inferiore o uguale a 250
B = avere un fatturato maggiore o uguale a 5000
a) Calcolare:
̅ ,
̅⁄
⁄ ,
⁄ ,
,
,
,
⋂ ,
⋃ ,
b) Verificare se e perché A e B sono incompatibili
c) Verificare se A e B sono indipendenti.
2. La tabella seguente mostra il numero di giorni, in un periodo di 50 giorni, durante i quali sono
avvenuti, in una certa città, X incidenti automobilistici. Adattate una distribuzione di Poisson alla
distribuzione data.
Numero di
Numero di
incidenti
giorni
0
21
1
18
2
7
3
3
4
1
3. I negozi A e B della catena YX di elettrodomestici hanno rispettivamente scorte settimanali di 30
e 20 forni a microonde. Supponiamo che la domanda settimanale di questi elettrodomestici segue la
distribuzione normale nel negozio A con media 25 e scarto quadratico medio 5; nel negozio B con
media 16 e sqm 3,5. Con queste informazioni, il management vuole sapere quale dei due negozi ha la
maggiore probabilità di esaurire le scorte di magazzino.
4. Da un’indagine è emerso che alcune caratteristiche socio-demografiche influenzano la percezione
che gli italiani hanno della pressione fiscale. In generale è emerso che il 60% di essi ritiene che la
pressione fiscale sia troppo elevata mentre il 40% l’ha definita giusta. Un gruppo di ricercatori vuole
verificare se il livello di reddito influisca su tale percezione. Un campione di 1005 intervistati è stato
suddiviso in due gruppi: il primo ha un reddito annuo inferiore a 50.000 euro e il secondo superiore a
50.000 euro annui.
Pressione
Reddito annuo
Fiscale
< 50.000 euro
> 50.000
Totale
225
180
405
Giusta
Troppo elevata
280
320
600
Totale
505
500
1005
1
a) Vi è differenza sulla percezione della pressione fiscale tra i due gruppi di reddito (α = 0,05)?
b) Calcolare il p-value e interpretarne il risultato.
5. L’azienda XYZ produce barre d’acciaio. Se il processo produttivo funziona in maniera corretta,
vengono prodotte barre d’acciaio di lunghezza media almeno pari a 2,8 metri. Le barre più lunghe di
tale misura possono ancora essere utilizzate, per esempio accorciandole, mentre le barre più corte
devono essere scartate. Si estrae un campione casuale di 25 barre la cui lunghezza media è pari a 2,73
metri e lo sqm campionario è di 0,20 metri. Vi è la necessità di aggiustare il processo di produzione?
a) Se si effettua un test per l’ipotesi nulla con un livello di significatività di 0,05, quale decisione si
dovrebbe prendere riguardo al processo produttivo?
b) Se si utilizza l’approccio del p-value quale decisione si dovrebbe prendere in merito al processo
produttivo?
c) Quale tipo di errore si può commettere e quali sono le conseguenze di tale errore?
SOLUZIONI I
Esercizio 1
Per utilizzare la tavola introdotta prima dobbiamo calcolare i totali marginali e poi calcolare le
frequenze relative, che diventano probabilità:
Capitale
Sociale
≤ 250
> 250
Totale
Fatturato
< 5000
80
90
170
Totale
≥ 5000
30
200
230
110
290
400
a) Usando la concezione classica di probabilità: casi favorevoli su casi possibili si ottiene:
110
̅
0,275; 1 0,275 0,725;
400
230
0,575; 1 0,575 0,425;
400
30
⋂
0,075;
400
⋃
̅⁄
⁄
⁄
⋂
⋂
⋂
0,275
0,575
30
110
0,273
30
230
0,13;
0,075
0,775;
⁄
1 0,13 0,87
Oppure
̅⋂
200
̅⁄
0,87
230
Si possono ottenere gli stessi risultati utilizzando il teorema delle probabilità totali.
1
2
b) Se A e B sono incompatibili deve essere
⋃
, cioè
si è visto prima,
⋂
0,075, per cui gli eventi sono compatibili.
⁄
c) Se A e B sono indipendenti, si ha
⁄
ma
0,130
0,275
⁄
e
0,273
0,575
per cui i due eventi sono dipendenti.
⁄
e
⋂
0 ma, come
La funzione di probabilità della v.c. di Poisson èPr
Pr
%!
%!
dove il parametro ' è sia la media che la varianza della stessa v.c., per cui per ottenere ' basta
calcolare la media aritmetica degli incidenti dalla tabella precedente.
∑ )* +*
0 ∗ 21
1 ∗ 18
2∗7
3∗3
4∗1
'
0,9
∑ +*
50
! " #$
Esercizio 2
! " #$
! " #$
,.! " #/,0
A questo punto nella distribuzione di PoissonPr
bisogna sostituire a X il
%!
%!
numero di incidenti per trovare le probabilità corrispondenti e il numero degli incidenti teorici. I
calcoli sono presentati nella tabella successiva.
Numero di incidenti
0
1
2
3
4
Pr (X incidenti)
0,4066
0,3659
0,1647
0,0494
0,0111
Valori teorici
20,33 o 20
18,30 o 18
8,24 o 8
2,47 o 2
0,56 o 1
Valori osservati
21
18
7
3
1
Da notare che l’adattamento della distribuzione di Poisson alla distribuzione data è piuttosto buono.
Nella distribuzione di Poisson la varianza è '. Il calcolo della varianza della distribuzione data
fornisce il valore 0,97 che è molto prossimo al valore trovato (0,90) e ciò può essere considerata
come una ulteriore prova della bontà di adattamento della distribuzione di Poisson alla distribuzione
campionaria data.
Esercizio 3
Per risolvere il problema è necessario calcolare la probabilità di esaurimento delle scorte del negozio
A utilizzando la distribuzione normale con media 25 e sqm 5 e calcolandone l’area a destra di 30.
Analogamente, per il negozio B si può trovare l’area a destra di 20 sottesa alla distribuzione normale
con media 16 e sqm 3,5. Infine, si devono confrontare queste due probabilità per vedere in quale
negozio risulta esservi una maggiore probabilità di esaurimento scorte di magazzino.
Per il negozio A, standardizzando il valore 30 otteniamo
) 2 30 25
1
1,00
3
5
Dalla Tavola della curva normale standardizzata troviamo che la P(z=1)=0,34134 per cui la
probabilità che ci interessa (nella coda destra) è 0,5 – 0,34134 = 0,15866;
3
Per il negozio B, standardizzando il valore 20 otteniamo
) 2 20 16
1
1,14
3
3,5
Dalla Tavola della curva normale standardizzata troviamo che la P(z=1,14)=0,37286 per cui la
probabilità che ci interessa (nella coda destra) è 0,5 – 0,37286 = 0,12714.
Quindi, il negozio A ha la maggiore probabilità di esaurire le scorte di forni a microonde.
Esercizio 4
Si tratta di un confronto tra due percentuali e il sistema d’ipotesi da sottoporre a verifica è
6 : 89 8:
5
69 : 89 8:
Le elevate numerosità giustificano il ricorso alla statistica test (normale standardizzata):
;
9
:
= 1>+9 1>+:
Poiché l’ipotesi alternativa è bidirezionale con α=0,05, i valori soglia sono – 1,96 e + 1,96; la regola
di decisione è: se il valore del test è interno all’intervallo – 1,96 e + 1,96 accetteremo l’ipotesi nulla;
se esterno la rifiuteremo.
Innanzitutto calcoliamo la stima della percentuale (proporzione), comune ad entrambe le popolazioni:
+9 9 +: : 280 320
0,5970
+9 +:
505 500
Dove
Quindi
:?
9
@ @
;
0,5545A
<= 1
9
:
= 1>+9
:
1>
+:
<= 1
:
@
0,64
0,5545
<0,5970 1
0,64
1
0,5970 B
505
1
C
500
2,7644
Decisione: poiché il risultato del test (-2,7644) è minore del valore soglia di sinistra (-1,96), si rifiuta
H0. C’è sufficiente evidenza per affermare che vi è differenza tra la popolazione di adulti che ritiene
che la pressione fiscale sia percepita diversamente tra i due gruppi di contribuenti.
Il p-value = 0,0057 (dalla tavola della curva normale standardizzata9. La probabilità che si verifichi
una differenza tra le popolazioni alla quale possa essere applicata una statistica test che si discosti da
zero per un valore uguale o maggiore di – 2,7644 in entrambe le direzioni è 0,0057, se non vi è
alcuna differenza nella popolazione di adulti che ritiene che i due gruppi di contribuenti percepiscano
in modo diverso la pressione fiscale.
Esercizio 5
Si tratta verifica d’ipotesi della media e il sistema d’ipotesi da sottoporre a verifica è
Il sistema d’ipotesi è 5
6 ∶ 2 2,80
69 ∶ 2 E 2,80
4
la statistica test da adottare per verificare l’ipotesi è
2
2,73 2,80
F
1,75
G
0,2
> +
>
√
√25
Dalla tavola della T di Student in corrispondenza di 24 gdl e di α=0,10 (l’ipotesi alternativa è
unidirezionale per cui per trovare il valore soglia di sinistra occorre raddoppiare il livello di
significatività), il valore soglia è – 1,711. Poiché il valore del test (-1,75) è inferiore al valore soglia,
si rifiuta l’ipotesi nulla. Quindi, bisognerà intervenire per aggiustare il processo produttivo.
Il p-value è inferiore al 5% ma superiore al 2,5 % (per la precisione è 0,0464) e la decisione
naturalmente non cambia.
L’errore che si può commettere è l’errore di I tipo, cioè rifiutare l’ipotesi nulla mentre in realtà è
vera. La conseguenza è quella di interrompere il processo produttivo per apportare gli opportuni
aggiustamenti, mentre in realtà non era necessario.
5
SIMULAZIONE II
1. Viene condotta un’indagine per studiare le scelte fatte nella selezione dei fondi comuni di
investimento. A studenti universitari e laureati sono stati presentati fondi comuni di investimento tutti
indicizzati sul FTSE MIB e tutti simili tranne i costi di gestione. I risultati parziali sono mostrati nella
seguente tabella:
Fondi di
investimento
Alti costi
Bassi costi
Studenti
Studenti univer
Laureati
27
18
73
82
a) Sapendo che uno studente è universitario, qual è la probabilità che scelga un fondo con alti costi
di gestione?
b) sapendo che uno studente sceglie un fondo con alti costi di gestione, qual è la probabilità che sia
universitario?
c) Spiegare la differenza nei risultati in a) e b).
d) I due eventi, “titolo di studio” e “scelta del fondo di investimento”, sono indipendenti?
(Giustificare la risposta).
2. Una teoria riguardante l’indice S&P 500 afferma che se l’indice chiude in rialzo la prima
settimana di contrattazioni dell’anno è probabile che l’indice presenti una performance positiva
nell’intero anno.
Dal 1950 al 2007, l’indice ha chiuso in rialzo nella prima settimana dell’anno per 38 volte. In questi
38 anni, per 32 volte l’indice ha avuto una performance annuale positiva. Qual è la probabilità che
l’indice abbia una performance annuale positiva per 32 anni su 38 se la probabilità che l’indice abbia
una buona performance è pari a :
a) 0,50
b) 0,70
c) 0,90
d) Sulla base dei risultati da a) a c), che idea ci si può fare in merito alla probabilità che l’indice in
questione abbia una performance annuale positiva se si osserva un guadagno nella prima settimana
dell’anno? Giustificare la risposta.
3. La tabella seguente mostra la statura di un campione di studenti. Adattate una distribuzione
normale alla distribuzione data.
Classi di
Studenti
statura
Fino a 155
15
155 - 165
40
165 - 175
80
175 - 185
48
Oltre 185
17
4. Due appezzamenti di uno stesso frutteto sono stati trattati con due diversi fertilizzanti. In ciascun
appezzamento è stato scelto a caso un campione di piante controllandone il peso della produzione.
6
1° campione 25,3 32,6 18,7 29,4
2° campione 31,5 23,4 29,2 34,6 27,5
Supponendo che nelle due popolazioni il peso della produzione abbia distribuzione normale:
a) Preliminarmente testare la uguaglianza delle due varianze al livello di significatività pari all’ 1%;
b) successivamente stabilire se tra i pesi medi vi è una differenza al livello di significatività pari al
5%.
5. L’ufficio del personale di una grande società intende stimare le spese dentistiche familiari dei suoi
impiegati per valutare la possibilità di attuare un programma di assicurazione per tali spese. Per un
campione di 40 impiegati si osservano le seguenti spese dentistiche (in euro) per l’anno passato:
110 362
246 185 510 208 173 425 316 179
210 160
230 230 220 222 278 325 222 224
90 150
190
85 330 238 143 224 134 178
150 125
110 125 115 313 170 254 126 115
a) Calcolate un intervallo di confidenza di livello 90% per la media delle spese dentistiche familiari
per tutti gli impiegati della società;
b) Calcolate un intervallo di confidenza di livello 95% per la media delle spese dentistiche familiari
per tutti gli impiegati della società;
c) La spesa media sostenuta dalla società nel precedente anno è stata di 250 euro. .Ritenete che ci
sia una differenza significativa rispetto alle spesa media dell’anno corrente?
SOLUZIONI II
Esercizio 1
Per utilizzare la tavola introdotta prima dobbiamo calcolare i totali marginali e poi calcolare le
frequenze relative, che diventano probabilità:
Fondi di
Studenti
investimento
TOTALE
Stud. Univer.
Laureati
Alti costi
27
18
45
Bassi costi
73
82
155
TOTALE
100
100
200
Usando la concezione classica di probabilità: casi favorevoli su casi possibili si ottiene:
:I
a) 9
0,27;
b)
:I
:IJ9?
0,6
c) Gli eventi condizionati sono in ordine inverso
d) Poiché Pr(scelta del fondo con alti costi di gestione/è un universitario)=0,27 non coincide con
Pr(scelta del fondo del fondo con alti costi di gestione /laureato) =0,225 I DUE EVENTI NON
⁄
SONO INDIPENDENTI ( ricordiamo che se A e B sono indipendenti, si ha
e
⁄
.
Esercizio 2
La v.c. che ci consente di calcolare le probabilità richieste è la Binomiale.
a) 8 0,50+ 38
7
38
L M 0,5N 0,5OPN 0,0001
)
Bisogna sostituire a x i valori che vanno da 32 a 38 e sommare le probabilità corrispondenti.
b) 8 0,70+ 38
38
Pr K 32
L M 0,7N 0,3OPN 0,03595
)
Bisogna sostituire a x i valori che vanno da 32 a 38 e sommare le probabilità corrispondenti.
c) 8 0,90+ 38
38
Pr K 32
L M 0,9N 0,1OPN 0,92005
)
Bisogna sostituire a x i valori che vanno da 32 a 38 e sommare le probabilità corrispondenti.
d) Sulla base dei risultati la probabilità che l’indice MIB abbia una prestazione positiva se si verifica
un rialzo iniziale nei primi cinque giorni di contrattazione è verosimilmente vicina a 0,90 e questo dà
luogo a una probabilità del 92% che in almeno 32 anni su 38 l’indice abbia una performance positiva
per tutto l’anno.
Pr
K 32
Esercizio 3
La funzione di densità di probabilità della v.c. Normale è
Y
A
R√:S
9
P
!#T U
UVU
dove il parametro 2 è la media e il parametro σ2 è la varianza (σ è lo scarto quadratico medio) della
stessa v.c.
Per adattare la distribuzione data ad una normale, occorre preliminarmente calcolare media e
varianza della distribuzione data.
Classi di
Studenti
Valore centrale
xi n i
(xi-µ)2ni
statura
150 – 155
15
152,5
2287,5
3828,009
155 – 160
40
157,5
6300,0
4818,025
160 – 175
80
167,5
13400,0
76,05
175 – 180
48
177,5
8520,0
3909,63
180 – 195
17
187,5
3187,5
6153,161
∑OìX9 )* +* 33695
168,5
+
200
∑ )* 2 : +* 18784,9
3:
93,9; 3 Y93,9 9,7
200
+
A questo punto occorre calcolare le aree al di sotto della curva normale per ognuna delle classi di
statura che rappresentano le rispettive probabilità:
9@@
NP] U
1
P
Pr ∞ [ [ 155
\
A :RU
P^ 3√28
Standardizzando, abbiamo
) 2
155 168,5
Pr B ∞ [ ; [
C Pr L ∞ [ ; [
M Pr ∞ [ ; [ 1,39
3
9,7
Dalla tavola B troviamo che P(z=-1,39)=0,41774;
per cui la probabilità cercata è 0,5 – 0,41774 = 0,08226.
Analogamente calcoliamo le altre probabilità:
2
8
)9
Pr B
[;[
):
2
\
9_@
9@@
1
3√28
A
P
A
P
NP] U
:RU
Pr L
Pr 165 [
)9
Pr B
[;[
2
2
\
9_@
1
3√28
)9
Pr B
2
2
0,36
NP] U
:RU
0,36 [ ; [ 0,69
168,5
185 168,5
[;[
M Pr 0,69 [ ; [ 1,70
3
3
9,7
9,7
Dalla tavola B troviamo che P(z=0,69)=0,25175; mentre P(z=1,70)=0,45543
per cui la probabilità cercata è 0,45543 - 0,25175 = 0,20368.
^
NP] U
1
P
Pr 185 [ [ ∞
\
A :RU
3√28
9?@
[;[
):
C
165
Pr L
[ 175
9I@
168,5
175 168,5
[;[
M Pr
9,7
9,7
3
3
Dalla tavola B troviamo che P(z=-0,36)=0,14058; mentre P(z=0,69)=0,25175
per cui la probabilità cercata è 0,14058 + 0,25175 = 0,39233.
9?@
NP] U
1
P
Pr 175 [ [ 185
\
A :RU
9I@ 3√28
2
):
C
155
[ 165
168,5
165 168,5
[;[
M Pr 1,39 [ ; [
3
3
9,7
9,7
Dalla tavola B troviamo che P(z=-1,39)=0,41774; mentre P(z=-0,36)=0,14058
per cui la probabilità cercata è 0,41774 – 0,14058 = 0,27716.
)9
Pr B
2
Pr 155 [
C
175
Pr L
168,5
[ ; [ ∞M
3
9,7
Dalla tavola B troviamo che P(z=1,70)=0,45543
per cui la probabilità cercata è 0,5 - 0,45543 = 0,04457.
[ ; [ ∞C
Pr L
185
Pr 1,70 [ ; [ ∞
Nella tabella seguente, riportiamo i dati utili per l’esercizio
Classi di statura
Pr (X studenti)
Valori teorici
Fino a 155
0,08226
16,5
155 - 165
0,27716
55,4
165 - 175
0,39233
78.5
175 - 185
0,20368
40,7
Oltre 185
0,04457
8,9
Valori osservati
15
40
80
48
17
Da notare che l’adattamento della distribuzione Normale alla distribuzione data è piuttosto buono.
Esercizio 4
Calcoliamo le medie e le varianze campionarie:
O`
∑ìX9
)9* 106
)̅9
26,5G9:
+9
4
∑ )9*
+9
)̅9
1
:
36,0
9
)̅:
U
∑OìX9
):*
+:
146
5
29,2G::
∑ ):*
+:
)̅:
1
:
17,7
a) Per poter supporre che le due varianze delle popolazioni siano ignote ma uguali, 39:
dobbiamo effettuare un test di confronto tra varianze.
6 ∶ 39: 3::
Il sistema d’ipotesi è 5
69 ∶ 39: 3::
Il test da utilizzare è a
b Ù
bUU
3::
3:
che rappresenta una v.c. F di Snedecor e Fisher con n1-1 e n2-1 gradi di
libertà, il cui risultato bisogna confrontarlo con il valore soglia dalla tavola della F in corrispondenza
della colonna con 3 gdl e la riga con 4 gdl.
Essendo il valore empirico a
b Ù
bUU
_,
9I,I
2,03 abbondantemente inferiore al valore soglia
F3,4,001=56,18, possiamo accettare tranquillamente l’ipotesi nulla e quindi supporre che le due
varianze siano uguali (omoschedasticità).
b) Prima di effettuare il test sulle medie occorre stimare la varianza comune attraverso la media
ponderata delle due varianze dei campioni:
c9: +9 1
c:: +: 1
36 3
17,7 4
c:
25,54
+9 +: 2
7
Quindi S = 5,05
Il sistema d’ipotesi è 5
6 ∶ 29
69 ∶ 29
2:
2:
Trattandosi di piccoli campioni, la statistica test da adottare per verificare l’ipotesi è
26,5 29,2
9
:
F
0,81
1
1
1
1
<
G<+
+: 5,05 4 5
9
Dalla tavola della T, in corrispondenza di 7 gradi di libertà e di un livello di significatività del 5%,
troviamo i valori soglia – 2,365 e + 2,365.
Decisione: poiché il valore empirico è interno ai valori soglia, si accetta l’ipotesi nulla. Tale
decisione è supportata dal valore del p-value, il quale è compreso tra il 40 e il 50%.
Non vi è differenza significativa di peso delle piante nei due appezzamenti.
Esercizio 5
Si tratta di determinare l’intervallo di confidenza della media con varianza ignota. La v.c. di
riferimento è la T di Student con n-1 gradi di libertà, ma trattandosi di grande campione, possiamo
tranquillamente fare riferimento alla v.c. normale standardizzata
Preliminarmente calcoliamo la media e la varianza campionarie:
∑ )* 8400
∑ )* )̅ : 334548
)̅
210;G :
8578,154;
+
40
+ 1
39
10
G
Y8578,154
92,6
a) L’intervallo cercato è
G
G
d 5)̅ 1e>:
[ 2 [ )̅ 1e>: f 1 g
√+
√+
92,6
92,6
d 5210 1,645
[ 2 [ 210 1,645
f 0,90
√40
√40
dh185,9 [ 2 [ 234,1i 0,90
Con una probabilità pari al 90% l’intervallo precedente potrebbe essere uno di quelli che contiene la
media incognita.
b) L’intervallo cercato è
G
G
d 5)̅ 1e>:
[ 2 [ )̅ 1e>: f 1 g
√+
√+
92,6
92,6
d 5210 1,960
[ 2 [ 210 1,960
f 0,95
√40
√40
dh181,3 [ 2 [ 238,7i 0,95
Con una probabilità pari al 95% l’intervallo precedente potrebbe essere uno di quelli che contiene la
media incognita.
6 : 2 250
c) Il sistema d’ipotesi è5
69 : 2 E 250
Il test da utilizzare è ;
)̅ 2
G
> +
√
210 250
92,6
>
√40
2,73
Dalla Tavola della curva normale standardizzata otteniamo: Pr(z=-2,73)=0,49683 per cui il p-value =
0,5 – 0,49683 = 0,00317. Con un p-value così basso, dobbiamo rifiutare l’ipotesi nulla. Rispetto alla
spesa media sostenuta lo scorso anno, quella dell’anno corrente sembra significativamente inferiore.
11
SIMULAZIONE III
1. In una catena di montaggio si eseguono due operazioni in sequenza. L'esito della prima non
dipende da quello della seconda. Le probabilità che le operazioni riescano senza difetti sono
rispettivamente 0.9 e 0.8. Calcolare la probabilità che:
a) nessuna delle due operazioni riesca;
b) almeno una delle due operazioni non riesca;
c) riesca esattamente una delle due.
2. Un’azienda deve verificare i propri ordini di vendita. Così vengono osservati n ordini presi a caso.
Secondo l’esperienza pregressa, la probabilità di avere un ordine errato è pari a 0,1. Come risulta
comprensibile, gli esiti di osservazioni diverse non si influenzano ovvero sono indipendenti. Si
calcoli:
a) la probabilità di osservare 3 ordini errati su 4;
b) la probabilità di osservare almeno 3 ordini errati su 4;
c) la probabilità di osservare meno di 3 ordini errati su 4;
3. Un produttore di cosmetici ha 1500 venditori porta a porta, che mediamente nell’ultimo mese
hanno realizzato vendite per un valore pari a µ = 3100 €, con uno s.q.m. σ = 700 €. Se si estrae un
campione di 36 venditori, qual è la probabilità che questo gruppo abbia realizzato nell’ultimo mese
a) Vendite per un valore inferiore a 3000 €;
b) Vendite per un valore compreso tra 2900 e 3300 €;
c) Vendite per un valore non inferiore a 2800 €.
d) Come cambierebbero le probabilità se il campione fosse di 64 venditori.
4. Un ricercatore di mercato per una società di prodotti elettronici intende studiare il tempo che i
residenti di una piccola città dedicano alla televisione. Si seleziona un campione di 50 intervistati e a
ciascuno si chiede di registrare in maniera dettagliata quanto guardano la televisione durante una
settimana. Si ottengono i seguenti risultati:
- Tempo dedicato alla televisione in una settimana: )̅ 15,3jdA, G 3,8jdA
- 25 intervistati guardano la televisione almeno 3 sere.
Sulla base di questi risultati, si determini:
a) un intervallo di confidenza al 95% per stimare il numero medio di ore dedicato alla televisione alla
settimana in questa città;
b) un intervallo di confidenza al 95% per stimare la percentuale di soggetti che guarda la televisione
almeno per tre sere alla settimana.
5. Una banca deve fare in modo che i suoi bancomat contengano l’ammontare di contante necessario
per far fronte ai prelievi dei suoi clienti. Tuttavia, se viene immobilizzato un ammontare eccessivo di
contante, la banca deve rinunciare a effettuare degli investimenti e a realizzare i relativi interessi.
Supponete che l’ammontare medio settimanale di denaro prelevato (per cliente) dal bancomat di una
filiale sia uguale a 160 € con uno scarto quadratico medio della popolazione uguale a 30 €.
a) Specificate l’ipotesi nulla e l’ipotesi alternativa;
b) Se, per un campione di 36 clienti, si osserva che la media campionaria dei prelievi è uguale a 172
€, si può concludere che la media dei prelievi non è uguale a 160 €? (usate un livello di significatività
pari a 0,05);
c) Come rispondereste al punto b) se lo scarto quadratico medio fosse uguale a 24 €?
d) Calcolando il p-value cambia la decisione assunta nei punti b) e c)?
12
SOLUZIONI III
Esercizio 1
Poniamo:
Ri = l'operazione i-esima riesce; R i = l'operazione i-esima non riesce.
a) Si deve calcolare
P ( R1 ∩ R2 )
Poiché gli eventi sono indipendenti avremo:
P ( R1 ∩ R 2 ) = P ( R1 ) + ( R 2 )
ma
k*
1
k*
per cui:
k9 ∩ k:
k9 ∙ k:
1 0.9 ∙ 1 0.8
1 ∙ 0.2 0.02
b) Dobbiamo calcolare la probabilità che non ne riesca almeno una, cioè: o non riesce una, o non
riesce l'altra, o non riescono entrambe ossia:
k9 ∪ k:
Soluzione 1 Per il teorema delle probabilità totali avremo che:
k9 ∪ k:
k:
0.1 0.2 0.02 0.28
k9
k9 ∩ k:
c) Ne riesce solo una, o l'una o l'altra, in simboli:
k9 ∪ k:
k9 ∩ k:
Soluzione 1 Per il teorema delle probabilità totali scriviamo
k9 ∪ k:
k9
k:
k9 ∩ k:
0.9 0.8
per cui la probabilità cercata sarà:
k9 ∪ k:
k9 ∩ k:
0.98
0.9 ∙ 0.8
0.8 ∙ 0.9
0.26
0.98
Esercizio 2
Per calcolare le probabilità richieste dobbiamo utilizzare la v.c. Binomiale la cui funzione di
probabilità è Pr
pONq8 N 1 8 OPN
π = 0,1;
1 – π = 0,9;
n=4
a)
b)
c)
Pr )
3
Pr ) K 3
Pr ) E 3
4
B C 0,1 ∙ 0,99 r, rrst
3
Pr ) 3
d ) 4
0,0036
Pr )
0
vjwA d )
d )
1
0,0001 r, rrsu
4
4
B C 0,1 ∙ 0,9
0,0001
4
d ) 2
0,6561 0,2916
0,0486
r, xxts
Esercizio 3
Si tratta di calcolare la probabilità che la media di un campione assuma un determinato valore. La
distribuzione campionaria della media, essendo un campione di grandi dimensioni, secondo il
3 :> , per cui
teorema del limite centrale assume forma normale con y
2Awzd
+
standardizzando abbiamo:;
N̅ P]
.
R
> O
√
13
a)
b)
2
c)
) [ 3000
2900 [ ) [ 3300
r, x}r~t
) K 2800
d) cA+
e)
a)
2
b)
{1 [
{1 K
64, z‚‚ƒz„j:
) [ 3000
{1 [
2900 [ ) [ 3300
r, xuu€
) K 2800
{1 K
I
P 9
>
√ _
{
:?
I
I
P 9
P 9
>
√ _
>
√ _
P 9
>
√_
{
:?
I
:.
I
:.
I
P 9
>
√_
P 9
>
√_
0,85|
[1[
2,57|
1,14|
[1[
3,42|
I
I
0,5
0,30234
r, •
r, €x€x•
P 9
>
√ _
|
1,71 [ 1 [ 1,71
0,5
0,37076
r, •
r, €xxt~
P 9
>
√_
r, }xutt
|
r, xx€x•
r, }•x•€
2,28 [ 1 [ 2,28
r, xxxt~
0,45543 ∗
0,48870 ∗
Esercizio 4
a) Si tratta di determinare l’intervallo di confidenza della media con varianza ignota. La v.c. di
riferimento è la T di Student con n-1 gradi di libertà, ma trattandosi di grande campione, possiamo
tranquillamente fare riferimento alla v.c. normale standardizzata
L’intervallo cercato è
G
G
d 5)̅ 1e>:
[ 2 [ )̅ 1e>: f 1 g
√+
√+
3,8
3,8
d 515,3 1,96
[ 2 [ 15,3 1,96
f 0,95
√50
√50
dh14,25 [ 2 [ 16,36i 0,95
Con una probabilità pari al 95% l’intervallo precedente potrebbe essere uno di quelli che contiene la
media incognita.
b) Si tratta di determinare l’intervallo di confidenza della percentuale. La v.c. di riferimento è la
Binomiale, ma trattandosi di grande campione, per il teorema di DeMoivre-Laplace, possiamo fare
riferimento alla v.c. normale standardizzata.
L’intervallo di confidenza della percentuale per grandi campioni è:
1
g
Pr …=
= 1
1e>: †
+
=
[8[=
= 1
1e>: †
+
=
‡
p=3/25=0,12
Pr …
0,12
1,96†
0,12 1 0,12
[ 8 [ 0,12
50
d 0,03 [ 8 [ 0,21
1,96†
0,95
0,12 1 0,12
‡
50
0,95
Con una probabilità pari al 95% l’intervallo precedente potrebbe essere uno di quelli che contiene la
percentuale incognita.
14
Esercizio 5
Si tratta della verifica d’ipotesi per la media.
Il sistema d’ipotesi è
a) 5
6 : 2 160
69 : 2 ˆ 160
b) Il test da utilizzare è
;
)̅ 2
3
> +
√
172 160
30>
√36
2,4
Nella tavola della curva normale standardizzata in corrispondenza di α=0,05 il valore soglia è 1,645
(trattandosi di una verifica con l’ipotesi alternativa unidirezionale destra, occorre considerare 2 volte
α). Essendo il valore del test superiore al valore soglia, si rifiuta l’ipotesi nulla, ovvero la media dei
prelievi (172 €) è significativamente diverso dalla media supposta, per cui la banca dovrebbe
aumentare l’ammontare di contante nel bancomat.
c)
;
N̅ P]/
R
> O
√
9I:P9_
: >
√ _
3
Questo risultato conferma ancora di più la decisione di rifiutare l’ipotesi nulla.
d) Il p-value nel caso c) è 0,0082, mentre nel caso c) è 0,00135. In ambedue i casi la probabilità di
commettere l’errore di I tipo (rifiutare l’ipotesi nulla mentre in realtà è vera) è così bassa per cui la
decisione di rifiutare l’ipotesi nulla risulta corretta.
15
SIMULAZIONE IV
1. Un investitore deve scegliere tra tre portafogli alternativi (A, B e C). Nella seguente tabella sono
riassunti i profitti (in euro) stimati dei portafogli alternativi sotto tre diverse condizioni economiche:
recessione, stabilità, espansione.
Portafogli alternativi
B
C
-2000
-7000
2000
-1000
5000
20000
assegna le seguenti probabilità a ciascuna situazione
Evento
A
Recessione
500
Stabilità
1000
Espansione
2000
Sulla base della sua esperienza l’investitore
economica:
Pr(recessione) = 0,30
Pr(stabilità) = 0,50
Pr(espansione) = 0,20
a) Determinare la migliore scelta di portafoglio dell’investitore in base al valore atteso;
b) Calcolare lo scarto quadratico medio per ciascuna scelta di portafoglio;
c) Alla luce di questi ultimi risultati, quale portafoglio siete portati a suggerire all’investitore?
Perché?
2. Per i fast-food, la precisione nella registrazione degli ordini nel servizio di asporto in auto è un
elemento di fondamentale importanza. Ogni mese, una rivista specializzata pubblica i risultati della
sua indagine. La precisione delle ordinazioni viene misurata attraverso la percentuale di ordini
compilati correttamente. Recentemente, la percentuale di ordini compilati correttamente nelle catene
di un fast-food è stata approssimativamente del 91%. Se viene preso un campione di tre ordini.
a) Quali sono la media e lo scarto quadratico medio della distribuzione relativi al numero di ordini
compilati correttamente?
b) Supponiamo che tre amici, in modo indipendente vadano al fast-food ed effettuino una
ordinazione di asporto in auto, qual è la probabilità che gli ordini siano compilati correttamente?
c) qual è la probabilità che nessuno degli ordini siano compilati correttamente?
d) qual è la probabilità che almeno due degli ordini siano compilati correttamente?
3. La XYZ Resort è una catena di 5 alberghi esclusivi situati in 2 isole. In una delle due isole, la
XYZ Resort possiede due alberghi, Levante e Ponente. Si è interessati a valutare il livello di
soddisfazione della clientela, dal quale si può dire dipenda il futuro dell’attività. Per questo motivo, il
responsabile dei rapporti con i clienti decide di far compilare ai clienti un questionario di valutazione
del servizio. In particolare, l’attenzione è concentrata su una domanda:”Hai intenzione di visitare di
nuovo il nostro albergo?” I risultati del questionario sono di 163 clienti disposti a ritornare su 227 nel
primo albergo (Levante) e 154 su 262 nel secondo albergo (Ponente). Attraverso l’interpretazione del
p-value, si può affermare che esiste una differenza tra i livelli di soddisfazione nei due alberghi
(misurata dall’intenzione di tornare nell’albergo)?
4. Di seguito sono riportati i dati relativi al costo del pernottamento in hotel e al costo dell’affitto di
un’auto durante una settimana per 20 città italiane.
16
Città
Hotel
Auto
Milano
283
47
Torino
179
41
Genova
185
49
Firenze
210
38
Aosta
128
32
Trieste
145
48
Verona
177
49
Trento
117
41
Venezia
221
56
Modena
159
51
Bologna
205
50
Ancona
128
32
Perugia
165
34
Roma
269
69
Napoli
198
41
Bari
158
40
Potenza
132
39
Palermo
205
47
Reggio Calabria
180
46
Cagliari
204
40
a) Costruire un intervallo di confidenza al 95% per il costo medio di pernottamento in Hotel;
b) Costruire un intervallo di confidenza al 95% per il costo medio di affitto di un auto;
5. Nelle informazioni nutrizionali stampate su una lattina di 400 ml di una bibita dietetica, si afferma
che vi sono soltanto 35 mg di sodio. Per affermare legittimamente ciò, si mantiene il contenuto di
sodio nell’acqua a µ = 34,5 mg. e σ = 0,24 mg. Durante i regolari controlli di qualità, si selezionano
casualmente dieci lattine della linea di produzione e tra le altre analisi, se lo scarto quadratico medio
del campione è significativamente maggiore (con α = 0,05) di 0,24 mg, la linea di produzione viene
fermata e il dosaggio del processo viene riaggiustato. Effettuando il controllo si riscontra s = 0,29
mg, si determini se è necessario il riaggiustamento.
SOLUZIONI IV
Esercizio 1
a) E(X1) = Σ x1ipi = 0,30*500 + 0,50*1000 + 0,20*2000 = 1050
E(X2) = Σ x2ipi = 0,30*(-2000) + 0,50*2000 + 0,20*5000 = 1400
E(X3) = Σ x3ipi = 0,30*(-7000) + 0,50*8-1000) + 0,20*20000 = 1400
Considerando il valore atteso dei tre portafogli, il maggiore profitto si ottiene dai portafogli B e C.
b) 39
<∑p)9*
y
9
:
q =*
17
3:
3
Y 500
1050
<∑p):*
y
*
y
Y
2000
<∑p)
:
:
:
∗ 0,30
1000
1050
∗ 0,30
2000
1400
q =*
1400
:
:
q =*
:
∗ 0,50
2000
1050
∗ 0,50
5000
1400
:
:
∗ 0,20
522,02
∗ 0,20
2.497,99
:
Y 7000 1400 : ∗ 0,30
1000 1400 : ∗ 0,50
20000 1400 : ∗ 0,20 9.656,09
c) La variabilità calcolata mostra come i tre portafogli alternativi sono molto diversi. Per questo
occorre distinguere gli investitori in: propensi, contrari o neutrali al rischio.
L’investitore con una bassa o nulla propensione al rischio dovrebbe scegliere il portafoglio A che,
pur avendo un rendimento assai minore rispetto agli altri, presenta una variabilità contenuta. Il
contrario avviene per i portafogli B e C che hanno un rendimento atteso più alto ma con una
variabilità elevata e quindi con un rischio più forte, soprattutto per il portafoglio C.
Esercizio 2
La v.c. da utilizzare è la Binomiale la cui funzione di probabilità è Pr
π = 0,91;
1 – π = 0,09;
n=3
a) 2 y
3 0,91
•, us;
Y+8 1 8
Y3 0,91 0,09
3 Y‰zd
b) Pr
c) Pr
3
0
dp q0,91 0,09
!
! P !
!
dp q0,91 0,09
! P !
d) Pr K 2
Pr
2
Pr
3
:
9
2
dp:q0,91 0,09
dove Pr
!
dove
e
Abbiamo, quindi:
;
=9
;
=
163
227
9
+9
r, u•st
0,09
r, rrru
5
6 : 89
69 : 89
<= 1
OPN
=9
8:
8:
=:
1
= B+
9
0,718=:
:
+:
0,718
<0,648 1
r, €x•u
8
0,2236 0,7536 r, xuu•
0,91: 0,099 0,2236
! P: !
Esercizio 3
Si tratta di un confronto tra due proporzioni.
Il sistema d’ipotesi è
Il test è
0,91
pONq8 N 1
163
227
154
262
0,588
1
0,648 B227
1
+: C
154
262
0,588
0,648
1
262C
3,01
18
Il p-value quando Z=3,01 è pari a 0,00262. Questo indica che se H0 fosse vera (cioè se le due
proporzioni fossero uguali tra loro), la probabilità che la realizzazione della statistica Z sia inferiore a
-3,01 è pari a 0,00131, e la probabilità di osservare una statistica Z maggiore di +3,01 è di 0,00131
(ricordiamo che quando il test è a due code o bidirezionale, il p-value si ottiene sommando le due
probabilità ottenute 0,00131*2=0,00262). In altre parole, essendo il p-value molto basso (inferiore al
0,2%) bisogna rifiutare l’ipotesi nulla: esiste una differenza significativa tra le due proporzioni e,
quindi, tra i livelli di soddisfazione dei clienti nei due hotel; la proporzione di clienti soddisfatti del
Levante è maggiore della proporzione di clienti soddisfatti nel Ponente.
Esercizio 4
a) Calcoliamo la media e la varianza campionarie delle spese di pernottamento:
O
∑ìX9 )* 3648
∑ )* )̅ :
37236,8
)̅
182,4G : 1959,832
+
20
+
1
19
La v.c. di riferimento è la T di Studenti con 19 gradi di libertà, la quale con un livello di confidenza
del 95% presenta i valori -2,093 e +2,093.
L’intervallo cercato è
G
G
Pr L)̅ Še,OP9
[ 2 [ )̅ Še,OP9 M 1 g
:
:
√+
√+
Pr L182,4
2,093
44,27
√20
[ 2 [ 182,4
d 161,68 [ 2 [ 203,12
2,093
44,27
M
√20
0,95
0,95
b) Calcoliamo la media e la varianza campionarie del costo d’affitto dell’auto:
O
∑ìX9 )* 900
∑ )* )̅ :
1910
)̅
45G : 100,53
+
20
+
1
19
La v.c. di riferimento è la T di Studenti con 19 gradi di libertà, la quale con un livello di confidenza
del 95% presenta i valori -2,093 e +2,093.
L’intervallo cercato è
G
G
Pr L)̅ Še,OP9
[ 2 [ )̅ Še,OP9 M 1 g
:
:
√+
√+
Pr L45
2,093
10,03
√20
[ 2 [ 45
2,093
d 40,31 [ 2 [ 49,69
10,03
M
√20
0,95
0,95
Esercizio 5
Si tratta di una verifica d’ipotesi sulla varianza:
6 : 3 : 0,24:
d) Il sistema d’ipotesi è5
69 : 3 : ˆ 0,24:
Il test da utilizzare è 19
‹:
+
1 G:
3:
10
1 0,29:
0,24:
13,14
Dalla Tavola della vc. χ2 in corrispondenza di 9 gradi di libertà e α=0,05 (ipotesi alternativa
unidirezionale destra) il valore soglia è 16,92. Per cui si accetta l’ipotesi nulla in quanto il valore del
test è inferiore al valore soglia. Non c’è alcuna evidenza empirica ad un livello di significatività di
0,05 che lo scarto quadratico medio campionario sia maggiore di quello richiesto. Quindi non è
necessario alcun aggiustamento del processo di produzione.
20
SIMULAZIONE V
a) Un’azienda produce DVD che hanno probabilità 0,02 di essere difettosi, indipendentemente l’uno
dall’altro. La confezione di vendita contiene 20 pezzi presi a caso dalla produzione totale. La
garanzia afferma che se è presente più di un pezzo difettoso la scatola verrà restituita.
a. Che percentuale di confezioni si prevede ritornerà?
b. Se compro 5 confezioni con che probabilità ne dovrò restituire una?
c. Qual è la probabilità che in tutte le confezioni non ci siano DVD difettosi?
d. Se ne compro 10 con che probabilità ne dovrò restituire una?
b) Ad una prova di concorso, il voto medio dei partecipanti è stato di 72 e lo scarto quadratico medio
9. I voti si distribuiscono secondo la legge normale. Calcolate la probabilità che:
a) Un partecipante abbia conseguito una voto minore di 65;
b) Un partecipante abbia conseguito un voto compreso tra 65 e 75;
c) Un partecipante abbia conseguito un voto non minore di 70;
d) Considerando che il migliore 10% dei partecipanti sarà promosso, qual è il voto minimo che un
partecipante deve ottenere per superare la prova?
c) In un fabbrica di generi alimentari, si vuol determinare il valore medio di “grasso totale” (in
grammi) in una confezione regolare di patatine. Si analizza un campione di 51 sacchetti e si
ottengono i seguenti risultati :)̅ 18.2ŒG : 0.56Œ: . Assumendo che la popolazione di tali
misurazioni sia distribuita normalmente, si determini:
a) L’intervallo di confidenza della media con un livello di confidenza pari a 0,90;
b) L’intervallo di confidenza della varianza con un livello d confidenza pari a 0,90.
d) Nel passato una macchina ha prodotto rondelle aventi uno spessore di 0,127 cm. Per determinare
se la macchina è a punto, viene estratto un campione di rondelle che fornisce i seguenti dati:
0,140 0,126 0,140 0,138 0,126 0,138 0,139 0,138 0,140 0,125
Provate l’ipotesi che la macchina sia a punto usando un livello di significatività dell’1%. Sulla base
della decisione assunta, quale tipo di errore si può commettere?
e) Una società che produce batterie è interessata al confronto tra performance di due diverse batterie
per cellulari, una batteria Nickel-Cadmium e una batteria Nickel-Metal Hydride. Queste batterie
vengono testate su cellulari della stessa marca, e si valuta per ciascuna il tempo di carica.
Nickel-Cadmium
Nickel-Metal Hydride
54,5
71,0
67,0
78,3
103,0
79,8
67,8
41,7
56,7
95,4
81,3
91,1
64,5
69,7
86,8
69,4
46,4
82,8
70,4
75,4
74,9
87,3
82,3
71,8
72,5
81,0
76,9
62,5
83,2
77,5
64,9
40,8
104,4
85,0
85,3
74,3
83,3
90,4
82,0
85,3
85,5
86,1
72,8
71,8
58,7
72,1
112,3
74,1
72,2
74,4
77,9
41,1
77,5
71,0
68,8
66,6
65,8
66,4
88,9
59,6
a) Assumendo che le due popolazioni abbiano la stessa varianza, si può affermare che esiste una
differenza nei tempi medi di carica dei due tipi di batterie (α = 0,05);
21
b) Calcolare il p-value e interpretare il valore.
SOLUZIONI V
Esercizio 1.
Il numero dei pezzi difettosi in una scatola di 20 DVD, segue la distribuzione Binomiale con
8 0,02:
+
B C 8N 1
)
Pr
Così abbiamo:
a) P(X>1) = 1 – P(X=0) – P(X=1)
: !
0,02 1 0,02 : P
=1
! : P !
: !
9! : P9 !
0,029 1
8
OPN
0,02
: P9
0,06
b) Ogni scatola viene resa con probabilità pari a circa 0,06. Allora se compriamo 5 scatole la
probabilità di renderne una sarà:
5
Pr
1
L M 0,069 1 0,06 @P9 0,234
1
c) La probabilità che in tutte le scatole non ci siano DVD difettosi è:
5
Pr
0
L M 0,06 1 0,06 @ 0,733
0
d) Su 10 confezioni la probabilità di restituirne una è:
10
Pr
1
L M 0,069 1
1
Esercizio 2.
a)
) [ 65
B1 [
_@PI:
.
_@PI:
0,78C
0,5
0,06
0,28230
9 P9
0,348
r, •}uu
b) 65 [ ) [ 75
B . [1[ . C
0,78 [ 1 [ 0,33
0,28230 0,12930
r, €}}t
I PI:
c) ) K 70
B1 K .
0,22C 0,5 0,0878 r, •~u~
d) Bisogna calcolare la votazione che individua l’ultimo 10% della distribuzione. Dalla tavola della
curva normale standardizzata occorre trovare il valore di z quando la Pr=0,40:
1 1,285=Ad•Žƒ) 2 13 72 1,285 ∗ 9 83,565 ~€
I@PI:
22
Esercizio 3.
a) Si tratta di determinare l’intervallo di confidenza della media con varianza ignota. La v.c. di
riferimento è la T di Student con n-1 gradi di libertà; ma, trattandosi di grande campione, possiamo
fare riferimento alla curva normale standardizzata. L’intervallo cercato è:
G
G
d 5)̅ 1e>:
[ 2 [ )̅ 1e>: f 1 g
√+
√+
Y0,56
Y0,56
d •18,2 1,645
[ 2 [ 18,2 1,645
• 0,90
√51
√51
dh18,03 [ 2 [ 18,37i 0,90
Con una probabilità pari al 90% l’intervallo precedente potrebbe essere uno di quelli che contiene la
media incognita.
b) Si tratta di determinare l’intervallo di confidenza della varianza con media ignota. La v.c. di
riferimento è la ‹ : con n-1 gradi di libertà.
L’intervallo cercato è
d‘
G: + 1
G: +
:
[
3
[
:
‹OP9,e/:
‹:
d5
1
e
OP9,9P :
“
0,56 ∗ 50
0,56 ∗ 50
[ 3: [
f
67,505
34,764
dh0,41 [ 3 : [ 0,81i
1
g
0,90
0,90
Con una probabilità pari al 90% l’intervallo precedente potrebbe essere uno di quelli che contiene la
varianza incognita.
Esercizio 4.
Si tratta della verifica d’ipotesi per la media.
Il sistema d’ipotesi è
a) Il test da utilizzare è
6 :2
5
69 : 2
F
2
2
)̅ 2
G
> +
√
Preliminarmente occorre stimare la media e la varianza campionarie:
23
)̅
∑ )*
+
1,35
10
∑ )*
+
0,135;G :
F
)̅ 2
G
> +
√
)̅
1
0,00038
9
:
0,135 0,127
0,0065
”
√10
0,0000422; G
0,0065
3,88
Dalla tavola della T di Student in corrispondenza di 9 gradi di libertà e di α=0,01 troviamo i valori
soglia -3,25 e +3,25; per cui, essendo il valore del test maggiore del valore soglia di destra, possiamo
rifiutare l’ipotesi nulla, ovvero sarebbe consigliabile registrare la macchina, o almeno estrarre un
altro campione. Possiamo commettere un errore di I tipo ovvero rifiutare l’ipotesi nulla mentre in
realtà è vera.
Esercizio 5.
 H 0 : µ1 = µ 2

 H 1 : µ1 ≠ µ 2
Il sistema d’ipotesi è
Calcoliamo le medie e le varianze campionarie:
)̅9
)̅ :
La statistica test è Z =
Dove S 2 =
O`
∑ìX9
)9*
+9
U
∑OìX9
):*
+:
78,5G::
x1 − x 2
1
1 
S 2  + 
 n1 n2 
(n1 − 1) S12 + (n 2 − 1) S 22
=
n1 + n 2 − 2
∑ )9*
+9
70,9G9:
=
70,9 − 78,5
∑ ):*
+:
1 
 1
187,69 + 
 30 30 
n1
n2
i =1
i =1
)̅9
1
)̅:
1
:
165,8
210,3
= −2,165
∑ ( x1i − x1 ) 2 + ∑ ( x2i − x2 ) 2
n1 + n2 − 2
:
=
165,8(29) + 210,3(29)
= 187,69
58
La statistica, se è vera H0, si distribuisce approssimativamente come una t di Student con n1+n2-2
gradi di libertà. La t di Student in questo caso (grande campione) può essere approssimata ad una
normale standardizzata. Quando α = 0,05 z è compreso tra -1,96 e +1,96, per cui rifiuto H0.
Il P – value è = 0,5 – 048461 = 0,01539. Questo risultato ci suggerisce di rifiutare l’ipotesi nulla, in
quanto la probabilità di sbagliare (commettere l’errore di prima specie) è di poco superiore all’1,5%;
quindi possiamo afferma che i due tipi di batteria hanno una durata media diversa.
24
SIMULAZIONE VI
1) Si consideri la variabile casuale doppia (X,Y) con funzione di probabilità congiunta riportata nella
seguente tabella:
X
Y
1
2
4
6
1
0,1
0,05
0,05
0
3
0,05
0,2
0,1
0
5
0
0
0,2
0,25
a. Calcolare E(X), E(Y), Var(X), Var(Y) e Cov(X,Y).
b. Calcolare E(X/Y=4);
c. Considerando la v.c. combinazione lineare Z = 2X + 3Y, calcolare E(Z) e Var(Z).
totale
2) Nelle vendite per telefono si utilizza un sistema di chiamata casuale per contattare i numeri
dell’elenco telefonico. Una società per le interviste telefoniche riporta che la probabilità di trovare
qualcuno a casa effettuando una telefonata sia pari a 0,2. Le chiamate sono indipendenti. Un
venditore decide di effettuare cinque chiamate.
a) Qual è la probabilità che non riesca a trovare nessuno?
b) Qual è la probabilità che riesca a trovare esattamente 2 persone?
c) Qual è la probabilità che riesca a trovare non meno di 2 persone?
d) Quando vengono effettuate delle chiamate nella città di Bari, la probabilità di trovare qualcuno è
soltanto 0,08. Qual è la probabilità che, facendo le cinque chiamate a Bari, non si riesca a contattare
nessuno?
3) La distribuzione dei rendimenti annuali delle azioni è approssimativamente simmetrica e vicina ad
una distribuzione normale, con un rendimento medio annuo pari al 13% e deviazione standard circa
pari al 17%.
a) Qual è la probabilità che il rendimento medio annuo delle azioni per i prossimi anni sia superiore
al 15%?
b) Qual è la probabilità che sia inferiore al 10%?
c) Qual è la probabilità che sia compreso tra l’11% e il 15%?
d) Qual è la probabilità che sia non inferiore al 12%?
4) I produttori di bevande cercano nuove soluzioni per evitare che le bibite perdano dolcezza durante
la conservazione. Ci sono dei degustatori appositamente addestrati per verificare i livelli di dolcezza
prima dell’apertura e dopo un periodo di conservazione. Di seguito riportiamo le perdite di dolcezza
secondo 10 degustatori:
2,0
0,4
0,7
2,0
-0,4 2,2
-1,3 1,2
1,1
2,3
Questi dati evidenziano una reale perdita di dolcezza? (Suggerimento: il P-value ti consentirà di
rispondere a questo quesito).
25
5) Una macchina dovrebbe produrre pezzi il cui peso nominale è di 50g e con una varianza pari a
9,8g2. Sono stati scelti casualmente nella produzione di un particolare giorno 16 pezzi, i cui pesi sono
i seguenti:
44
42
46
52
48
52
48
52
46
48
51
48
48
44
52
44
Sapendo che gli scostamenti dei pesi effettivi dal peso medio si distribuiscono normalmente,
dire se la macchina in questione è stata ben tarata, sia per quanto riguarda il peso medio che la
varianza a livello di significatività del 5%.
SOLUZIONI VI
Esercizio 1
a)
E(X) = 1*0,2+3*0,35+5*0,45=3,5
E(Y) = 1*0,15+2*0,25+4*0,35+6*0,25=3,55
Var(X) = (1-3,5)2*0,2+(3-3,5)2*0,35+(5-3,5)2*0,45=2,35
Var(Y) = (1-3,55)2*0,15+(2-3,55)2*0,25+(4-3,55)2*0,35+(6-3,55)2*0,25=3,147
Cov(X,Y) = E(XY)-E(X)*E(Y)=
1*1*0,1+1*3*0,05+2*1*0,05+2*3*0,2+4*1*0,05+4*3*0,1+4*5*0,2+6*5*0,25)-3,5*3,55=2,025
b)
E(X/Y=4) = (1*0,05+3*0,1+5*0,2)/0,35=3,857
c)
E(Z) = E(2X+3Y) = E(2X) + E(3Y) = 2E(X) +3E(Y) = 2*3,5+3*3,55=17,65
Var(Z) = Var(2X+3Y) = Var(2X) + Var(3Y) = 22Var(X) + 32Var(Y) = 4*2,35 + 9*3,147 = 37,723
Esercizio 2
La funzione di probabilità della v.c. Binomiale è Pr
π = 0,2; 1 – π = 0,8;
c) Pr
Esercizio 3
a)
d ) ˆ 15
K2
pONq8 N 1
8
OPN
5
B C 0,2 ∙ 0,8@ r, s•ut~
0
5
b) Pr 2
B C 0,2: ∙ 0,8
r, •r€~
2
•Pr X 0
Pr X 1 — 1 •0,32768 0,4096—
5
0,4096
Dove Pr(X=1) = B C 0,29 ∙ 0,8
1
n=5
1
a) Pr 0
d) π = 0,08
1 – π = 0,92;
Pr 0
5
B C 0,08 ∙ 0,92@
0
d B1 ˆ 9I C
d 1 ˆ 0,11764 =
0,5
0,12
0,5 0,0478 r, €•••.
r, •t•u•
n=5
r, t•xr
9@P9
26
b) d ) E 10
0,5
d B1 E
C
d 1 E 0,17647
9I
0,18
0,5 0,0714 r, ۥ~t
9 P9
c) d 11 E ) E 15
dB
E1E
C
d 0,12 E 1 E
9I
9I
0,04776 ∗ 2 r, rxr••
9:P9
d) d ) ˆ 12
d B1 ˆ
C
d 1 ˆ 0,058 =
9I
0,5
0,05
0,5 0,01994 r, •}xx€
99P9
9@P9
0,12
Esercizio 4
Il sistema d’ipotesi è
H 0 : µ = 0

 H1 : µ ≠ 0
x =1,02 s2=1,1969
La statistica test è
T=
x − µ0
1,02 − 0
=
= 2,70
s
1,196
n
10
Il P-value per t=2,70 è l’area che sta a destra di tale valore della curva della distribuzione T di student
con 9 gdl. Non è possibile trovare il valore P esatto, tuttavia è possibile trovare i due valori vicini tra
loro tali che il P-value sia al loro interno.
Infatti:
α = 0,05 =>
t = 2,262
α = 0,02
=>
t = 2,821
Per cui il P associato a t=2,70 è compreso tra 5% e il 2%. In definitiva possiamo affermare che se
dovessimo rifiutare l’ipotesi nulla potremmo commettere un errore di I tipo inferiore al 5% e poco
superiore al 2%. Possiamo quindi dire che c’è una forte evidenza di perdita di dolcezza.
Esercizio 5
Il sistema d’ipotesi è 5
6 ∶ 2
69 ∶ 2
50
50
Occorre preliminarmente calcolare sia la media che lo scarto quadratico medio campionario:
27
)̅
∑OìX9 )*
+
765
16
€u, ~G
∑ )*
†
+
)̅
1
:
†
164,44
15
Y11,0
Quindi S = 3,3
Dato che il tempo X si distribuisce normalmente con σ ignoto, la statistica test da adottare per
verificare l’ipotesi è
2
47,8 50
F
2,64
G
3,3
> +
>
√
√16
La distribuzione T di Student in corrispondenza di 15 g.d.l. con α=0,05 presenta i valori soglia -2,13
e +2,13. Essendo -2,64 < -2,13 rifiutiamo l’ipotesi nulla, ovvero possiamo affermare che la macchina
non è ben tarata, con una probabilità di errore (I tipo) inferiore al 5%. (Il p-value calcolato con Excel
è 0,018558; quindi la probabilità di errore è inferiore al 2%).
Svolgiamo ora la verifica d’ipotesi sulla varianza:
6 : 3 : 9,8
Il sistema d’ipotesi è5
69 : 3 : ˆ 9,8
Il test da utilizzare è ‹:
+
3
1 G:
:
16
1 11
9,8
16,8
Dalla Tavola della vc. χ2 in corrispondenza di 15 gradi di libertà e α=0,05 (ipotesi alternativa
unidirezionale destra) il valore soglia è 24,996. Per cui si accetta l’ipotesi nulla in quanto il valore del
test è inferiore al valore soglia. Non c’è alcuna evidenza empirica ad un livello di significatività di
0,05 che lo scarto quadratico medio campionario sia maggiore di quello richiesto. Dal punto di vista
della variabilità non è necessario alcun aggiustamento del processo di produzione.
28
SIMULAZIONE VII
1. In una scarpiera ci sono 9 scarpe, di cui 2 scarpe sinistre e 7 scarpe destre. CalcolAre la probabilità
che:
a) Estratte casualmente due scarpe senza reimmissione, siano entrambe destre;
b) Estratte casualmente due scarpe con reimmissione, siano entrambe destre;
c) Estratte casualmente due scarpe senza reimmissione, una sia destra e l’altra sinistra;
d) Estratte casualmente tre scarpe senza reimmissione, siano tutte e tre sinistre;
e) Estratte casualmente tre scarpe con reimmissione, siano tutte e tre sinistre;
2. Se il 3% delle lampadine prodotte da una fabbrica è difettoso, trovate la probabilità che, in un
campione di 100 lampadine:
a. 0 lampadine siano difettose;
b. Al massimo 2 lampadine siano difettose;
c. Almeno 4 lampadine siano difettose;
d. Tra 1 e 3 lampadine siano difettose;
e. Determinare la media e la varianza della distribuzione delle lampadine difettose.
3. Supponete che il tempo necessario per ristrutturare un appartamento di 200 metri quadrati da parte
di una società di costruzioni sia distribuito secondo la legge normale con µ = 40 ore e con uno s.q.m.
σ = 5 ore. Calcolate:
a) La probabilità che la ristrutturazione sia completata in meno di 35 ore;
b) La probabilità che la ristrutturazione duri tra le 28 e 32 ore;
c) La probabilità che la ristrutturazione duri tra le 35 e 48 ore;
d) Il primo 20% dei progetti richiede un numero di ore pari almeno a?;
e) Cosa succede ai punti precedenti se σ = 10 ore.
4. Per le prossime elezioni c’è un nuovo candidato alla carica di presidente. Egli chiede ad una
società di sondaggi di opinione di condurre un sondaggio telefonico casuale su base nazionale per
determinare la percentuale di potenziali elettori che voterebbero per lui invece che per il presidente in
carica. A conclusione del sondaggio, la società ottiene i seguenti risultati:
- 384 voterebbero per il nuovo candidato;
- 545 per il presidente in carica;
- 139 sono ancora indecisi.
Sulla base di questi risultati,
a) si determini un intervallo di confidenza al 95% per la percentuale della popolazione dei potenziali
elettori per il nuovo candidato;
b) considerando che per vincere le elezioni è necessario almeno ottenere il 40% dei consensi,
verificare la possibilità del nuovo candidato di essere eletto sulla base dei sicuri elettori del
campione.
5. Un’azienda che fornisce energia elettrica è interessata a confrontare il consumo in elettricità nella
stagione estiva nelle casi uni-familiari di due province. Estratto un campione di case per ciascuna
provincia, si osservano i seguenti risultati:
29
™
˜
s
n
Provincia 1
115 €
30 €
25
Provincia 2
98 €
18 €
21
a. Si può affermare che la spesa media nella seconda provincia è maggiore di 80 €, al livello
dell’1%?
b. I dati evidenziano l’esistenza di una differenza fra le varianze delle spese nelle due province al
livello del 1%?
c. I dati evidenziano che le spese medie mensili sono maggiori nella prima provincia al livello del
1%?
SOLUZIONI VII
Esercizio 1
I
_
a) Pr(2 scarpe destre)=. š ?
b) Pr(2 scarpe destre)= š
.
?
I
I
0,5833
0,6049
c) Pr(1 destra e 1 sinistra)=. š ? . š ?
d) Pr(3 sinistre)=0
:
:
:
e) Pr(3 sinistre)=. š . š . 0,011
I
:
:
I
0,3889
Esercizio 2
)
AP
Trattasi di applicazione della v.c. binomiale, ma considerando che n è grande e p piccolo, possiamo
applicare la distribuzione di Poisson, la cui funzione di probabilità è:
!
N!
λ=n*p = 0,03*100 = 3, abbiamo:
a)
0
AP
/
!
0,049
b) P(x≤2) = ∑:NX A P
0
AP
2
/
!
1
AP
!
N!
0,049
AP
U
:!
c) P(x≥4) = 1 - ∑NX A P
0
1
AP
AP
/
!
`
9!
0,416
`
9!
0,147
0,220
!
N!
0,049
0,147
0,364
30
2
3
AP
1[)[3
d)
2
AP
:!
1
3
AP
U
AP
0,220
›
!
0,220
∑NX9 A P
AP
U
:!
`
9!
!
N!
0,587
0,147
0,220
›
!
0,220
e) µ = σ2 = λ = 3
Esercizio 3
La funzione di densità della v.c. normale è œ )
µ = 40 e σ = 5
a.
) [ 35
B1 [
1C
@P
@
:?P
9
R√:S
0,5
A
P
!#T U
UVU
0,34134
r, }•~tt
28 [ ) [ 32
B @ [1[ @ C
2,4 [ 1 [ 1,6
2,4
1,6
0,49180 0,44520 r, r€tt
@P
?P
35 [ ) [ 48
B @ [1[ @ C
1,0 [ 1 [ 1,6
1,0
1,6
c.
0,34134 0,44520 r, u~t•
NP]
d. ; ; ) μ 13;P(0,30) → z = 1,285
R
e. x = 40 – 0,845*5 = 35,775 ore
Con l’aumentare di σ, la curva si appiattisce per cui la probabilità in corrispondenza dei valori
centrali diminuisce, mentre quella delle code aumenta:
a) 0,308; b) 0,097; c) 0,4796; d) 31,55
b.
:P
Esercizio 4
a) L’intervallo di confidenza della percentuale per grandi campioni è:
1
n=384+545+139=1068
Quindi:
0,95
g
Pr …=
Pr …0,36
= 1
1e †
=
+
=
384
1068
[8[=
0,36
0,36 ∗ 0,64
1,96†
[ 8 [ 0,36
1068
r, x•
žŸ r, ss [
= 1
1e †
[ r, sx
+
1,96†
=
‡
0,36 ∗ 0,64
‡
1068
31
6 : 8 0,45
69 : 8 E 0,45
384
=
0,36
1068
b) Il sistema d’ipotesi è
Trattandosi di grandi campioni il test da utilizzare è:
;
=
<8 1
8
+
0,36
8
0,40
<0,40 0,60
1068
2,66
Il p-value, quando z=-2,66, è uguale a 0,00391 (0,5 – 0,49609). Dobbiamo rifiutare l’ipotesi con una
probabilità di sbagliare inferiore al 0,4%. Probabilmente il nuovo candidato non sarà eletto.
Esercizio 5
a) Si tratta della verifica d’ipotesi per la media.
Il sistema d’ipotesi è
5
Il test da utilizzare è
6 : 2 80
69 : 2 ˆ 80
)̅ 2
G
> +
√
F
98 80
18>
√21
4,58
Dalla tavola della T di Student in corrispondenza di 20 gradi di libertà e di α=0,02 (ricordiamo che
quando l’ipotesi alternativa è bidirezionale per trovare il valore soglia bisogna considerare 2α)
troviamo i valori soglia 2,528; per cui, essendo il valore del test maggiore del valore soglia, possiamo
rifiutare l’ipotesi nulla: l’evidenza empirica è a favore dell’ipotesi secondo cui la spesa media della
seconda provincia è maggiore di 80 €.
6 ∶ 39:
b) Il sistema d’ipotesi è 5
69 ∶ 39:
Il test da utilizzare è a
b Ù
bUU
9?
3::
3::
1,67
che rappresenta una v.c. F di Snedecor e Fisher con n1-1 e n2-1 gradi di libertà. Il risultato ottenuto va
confrontato con il valore soglia dalla tavola della F in corrispondenza della colonna con 24 gdl e la
riga con 20 gdl.
Essendo il valore empirico a 1,67 inferiore al valore soglia F24;20;0,01=2,78 possiamo accettare
l’ipotesi nulla: l’evidenza empirica non consente di concludere che le due varianze siano diverse tra
di loro.
32
 H 0 : µ1 = µ 2

 H 1 : µ1 > µ 2
La statistica test è (grandi campioni):
c) Il sistema d’ipotesi è
;
9
1
G<
+9
:
1
+:
dove
c:
c9: +9
1
+9
c:: +:
+: 2
G
115
1
25,3<
25
1
Y638,2
98
1
21
30: 24
25,3
44
2,27
18: 20
638,2
I valori soglia dalla tavola della curva normale standardizzata in corrispondenza di α=0,02 (ipotesi
alternativa bidirezionale per cui l’ α del problema viene preso due volte) sono -2,326 e +2,326.
Poiché il valore del test cade all’interno dell’intervallo dei valori soglia, l’ipotesi nulla non può essere
rifiutata: non si può quindi concludere che le spese medie nelle due province
33
SIMULAZIONE VIII
1.
In un’indagine si rileva in un collettivo di 2000 cittadini se hanno una casa di proprietà o
vivono in affitto e se si recano al lavoro in macchina oppure no. Questi sono i risultati:
Si reca al lavoro in
Casa di
Casa in
Totale
macchina
proprietà
affitto
Sì
824
681
1505
No
176
319
495
Totale
1000
1000
2000
a) Sapendo che un intervistato si reca al lavoro in macchina, qual è la probabilità che abbia
una casa di proprietà?
b) Sapendo che un intervistato ha una casa di proprietà, qual è la probabilità che si rechi al
lavoro in macchina?
c) Qual è la probabilità che un intervistato non si reca al lavoro in macchina e ha una casa
in affitto?
2. La quantità di liquido contenuta nelle bottiglie prodotte da un’azienda che produce
bevande analcoliche si distribuisce come una normale con µ = 2 litri e σ = 0,05 litri. Se
si estrae a caso una bottiglia, qual è la probabilità che quantità di liquido contenuta:
a) Sia compresa tra 1,90 e 2,10 litri?
b) Sia inferiore a 1,85 litri?
c) Sia non superiore a 2,05 litri?
d) Determinare il contenuto in litri superato dal 90% delle bottiglie;
e) Determinare l’intervallo centrato intorno alla media 2 litri, in cui cadono l’98% delle
bottiglie.
3.
Il manager che si occupa del controllo di qualità in un’azienda produttrice di lampadine
intende stimare la durata media di un grande carico di lampadine. Si sa che lo scarto
quadratico medio della durata delle lampadine è di 100 ore. Si estrae un campione di 64
lampadine e la media campionaria risulta pari a 350 ore.
a) Calcolate un intervallo di confidenza al 95% per la vera durata media delle lampadine
del carico;
b) E’ necessario supporre che la durata delle lampadine abbia distribuzione normale?
Spiegate.
c) Pensate che il produttore possa affermare che le lampadine durano in media 400 ore?
Spiegate.
4.
Una filiale di una banca in un quartiere commerciale di una città si è organizzata per
fornire maggiori servizi ai clienti durante l’orario di pranzo. E’ stato rilevato il tempo di
attesa (inteso come il tempo che un cliente passa da quando si è messo in fila fino a che
non raggiunge lo sportello) di tutti i clienti nell’arco di una settimana proprio nella
fascia oraria 12:00-13:00 e su un campione casuale di 15 clienti si sono ottenuti i
seguenti risultati:
4
.21
5
.55
4
.50
3
.02
6
.10
5
.13
0
.38
4
.77
5
.12
2
.34
6
.46
3
.54
6
.19
3
.20
3
.79
34
Con un livello di significatività di 0.05 vi è evidenza che il tempo medio di attesa risulta
inferiore a 5 minuti?
5. Un campione di 500 soggetti abitanti in un’area metropolitana viene sottoposto ad un
sondaggio in termini di consumo. Una delle domande è la seguente: “Ti piace fare
shopping per acquistare capi di abbigliamento?” Rispondono positivamente 136 uomini
su 240 e 224 donne su 260.
a) E’ possibile affermare ad un livello di significatività pari a 0,01 che esiste una differenza
significativa tra le proporzioni di uomini e donne a cui piace fare shopping?
b) Calcolate il p-value e interpretatene il risultato.
SOLUZIONI
Esercizio 1
a) P(casa di proprietà/si reca la lavoro in macchina) = 824/1505 = 0,5475;
b) P(si reca la lavoro in macchina/casa di proprietà) = 824/1000 = 0,8240
c) P(non si reca al lavoro in macchina e ha una casa in affitto) = 319/2000 = 0,1595.
Esercizio 2
La funzione di densità di probabilità della v.c. Normale è
NP] U
1
P
Y
A :RU 3√28
Per la distribuzione della quantità contenuta nelle bottiglie la media e lo scarto
quadratico medio sono rispettivamente:
μ 2; σ 0,05
A questo punto occorre calcolare le rispettive probabilità:
a) Pr 1,90 [
[ 2,10 Standardizzando, abbiamo:
1,90 2,00
2,10 2,00
Pr L
[;[
M
0,05
0,05
Pr
2[;[
2
Dalla tavola B troviamo che P(z=2)=0,4772;
per cui la probabilità cercata è 0,4772x2 = 0,9544.
35
b) Analogamente calcoliamo le altre probabilità: Pr
1,85 2,00
M
0,05
Pr L; [
[ 1,85
Pr Z [
3
Dalla tavola B troviamo che P(z=-3)=0,49865;
per cui la probabilità cercata è 0,5 - 0, 49865 = 0,00135
c) Pr
[ 2,05
Pr L; [
2,05 2,00
M
0,05
Pr Z [ 1
Dalla tavola B troviamo che P(z=1)=0,3413;
per cui la probabilità cercata è 0,5 + 0,3413 = 0,8413;
d)
e)
d
K)
0,90
Dalla tavola B troviamo che P(z)=0,40 quando Z = 1,285; per cui:
2 13 2 1,285 ∗ 0,05 }, xst
d )9 [ [ ):
0,98
Dalla tavola B troviamo che P(z)=0,49 quando Z = 2,325; per cui:
)9
):
2
2
13
13
2
2
2,325 ∗ 0,05
2,325 ∗ 0,05
}, ~~€
•, }}t
Esercizio 3
Trattasi di
L’intervallo è
a)
d £)̅
1e>:
costruzione dell’intervallo di confidenza della media con varianza nota.
R
√O
[ 2 [ )̅
d 5350
1e>:
1,96
R
√O
¤
100
√64
0,95
[ 2 [ 350
dh325,5 [ 2 [ 374,5i
1,96
100
√64
0,95
f
0,95
b) No. Essendo σ noto e n=64 (grande campione), per il teorema del limite centrale, la
distribuzione di è approssimativamente normale;
c) Non si può affermare che le lampadine durano in media 400 ore. Sulla base dei dati
campionari, un valore di 400 ore supera la media campionaria osservata, 350 ore, di 4 volte
lo scarto quadratico medio.
36
Esercizio 4
Il sistema d’ipotesi è 5
6 ∶ 2 5
69 ∶ 2 E 5
Occorre preliminarmente calcolare sia la media che lo scarto quadratico medio campionario:
)̅
∑OìX9 )*
+
64,3
15
†
€, •xG
∑ )*
+
)̅
1
:
37,56
†
14
Y2,68
Quindi S = 1,64
Dato che il tempo X si distribuisce normalmente con σ ignoto, la statistica test da adottare
per verificare l’ipotesi è
2
F
G
> +
√
4,29 5
1,64
>
√15
1,68
La distribuzione T di Student in corrispondenza di 14 g.d.l. con α=0,10 (ipotesi alternativa
unidirezionale) presenta il valori soglia -1,76. Essendo -1,68 > -1,76 accettiamo l’ipotesi nulla,
ovvero possiamo affermare che il tempo medio di attesa non è inferiore a 5 minuti.
Esercizio 5
a) Si tratta di un confronto tra due percentuali.
Il sistema d’ipotesi è
6 : 89
5
69 : 89
Il test è
;
dove
e
=9
Abbiamo, quindi:
=
136
240
9
+9
<= 1
8:
8:
=9
=:
1
= B+
9
0,567=:
:
+:
136
240
1
+: C
224
260
224
260
0,862
0,72
37
;
0,567
0,862
7,34
1
1
<0,72 1 0,72 B
240 260C
Quindi l’ipotesi nulla deve essere rifiutata in quanto il valore empirico (-7,34) è
notevolmente inferiore al valore soglia di sinistra (-2,58): esiste una differenza significativa
fra le proporzioni di uomini e donne che amano fare shopping.
b) Il p-value è prossimo a zero e di conseguenza la decisione assunta comporta un rischio di
errore quasi nullo.
38
Simulazione IX
1) Un’urna contiene tre palle rosse e due verdi. Si estraggono due palle a caso l’una dopo
l’altra a) reinserendo la prima e b) senza reinserire la prima. Definiamo le seguenti variabili
1GA¥z=dƒ„zèdjGGz
1GA¥zGA•j+vzèdjGGz
casuali:
5
§ £
0GA¥z=dƒ„zèwAdvA
0GA¥zGA•j+vzèwAdvA
Per i casi a) e b) definire
a) Le distribuzioni di probabilità congiunte;
b) Le distribuzioni di probabilità condizionate;
c) I valori attesi condizionati.
2) Supponete che in questo momento 10 persone siano collegate per l’acquisto di articoli su
internet. Sapendo che la probabilità che ciascuno dei 10 soggetti acquisti effettivamente 1
articolo è pari a 0,2, calcolate:
a) La probabilità che nessun soggetto acquisti un articolo;
b) La probabilità che due soggetti acquistino un articolo;
c) La probabilità che almeno due soggetti acquistino un articolo;
d) La probabilità che al massimo due soggetti acquistino un articolo
e) Se le persone collegate sono 20 calcolare la probabilità che 2 soggetti acquistino un
articolo.
3) La quantità di liquido X contenuto nelle bottiglie provenienti da una società che produce
bevande analcoliche si distribuisce con una normale con µ = 2 litri e σ = 0,05 litri. Le
bottiglie che contengono meno di 1,90 litri oppure più di 2,10 litri non possono essere
immessi sul mercato. Scelta a caso una bottiglia, calcolate la probabilità che:
a) Contenga una quantità di liquido compreso tra 1,90 e 2,00 litri;
b) Contenga una quantità di liquido compreso tra 1,90 e 2,10 litri;
c) Contenga una quantità di liquido inferiore a 1,90 o superiore 2,10 litri;
d) Su una produzione di 10000 bottiglie quante bottiglie potrebbero essere scartate;
4) Il responsabile delle vendite in una catena di supermercati vuole verificare se le vendite di
un giocattolo per animali domestici possono essere influenzate dalla posizione del giocattolo
sugli scaffali (posizione frontale, centrale, o posteriore). Considerato un campione di 18
punti vendita, le tre posizioni del giocattolo vengono sperimentate ciascuna in 6 punti
vendita scelti casualmente. Nella tabella sono rappresentate le vendite del prodotto in
ciascun punto vendita alla fine del periodo di prova.
FRONTALE
8,6
7,2
5,4
6,2
5,0
4,0
CENTRALE
3,2
2,4
2,0
1,4
1,8
1,6
POSTERIORE
4,6
6,0
4,0
2,8
2,2
2,8
a) Ad un livello di significatività pari a 0,05 si può affermare che esiste una differenza
significativa fra le vendite medie del prodotto ai diversi livelli del fattore;
39
b) Calcolando il p-value cambia la decisione?
c) Quali conclusioni dovrebbe trarre il responsabile alle vendite?
5) In una multinazionale di abbigliamento, la programmazione e il controllo dell’attività di
approvvigionamento richiede il continuo monitoraggio del numero dei capi venduti X. Si ha
ragione di ritenere che X si distribuisce normalmente con media µ e varianza σ2 incognite.
Si estrae un campione casuale di n = 9 negozi e si osservano per ognuno i seguenti capi
venduti:
190 220 188 187 193 215 207 190 210
Costruire l’intervallo di confidenza per il numero medio di capi venduti nella settimana dalla
catena di negozi, al livello del 98%.
SOLUZIONI
Esercizio 1
a) Le distribuzioni di probabilità congiunte, con e senza reinserimento, sono rispettivamente:
Y
X
Y
X
0
1
0
1
0
4/25
6/25
0
2/20
6/20
1
6/25
9/25
1
6/20
6/20
b) Nel caso di reinserimento le probabilità condizionate sono:
X
Px/0(xi)
X
Px/1(xi)
X
Py/0(yi)
0
2/5
0
2/5
0
2/5
1
3/5
1
3/5
1
3/5
X
0
1
Px/0(xi)
1/4
3/4
X
0
1
Px/1(xi)
1/2
1/2
X
0
1
Py/0(yi)
1/4
3/4
X
0
1
Py/1(yi)
2/5
3/5
X
0
1
Py/1(yi)
1/2
1/2
c) Infine, le medie condizionate sono nel caso di reinserimento e non reinserimento
rispettivamente pari a:
3
3
) 0
« ¬ 0
5
5
—
;
y•§|
;
y• |§—
3
ª3 ¬ 1
) 1
5
©5
y• |§—
3
¬
4
1
¬
2
0
; y•§| —
1
3
)
4
1
)
2
0
1
40
Esercizio 2
La funzione di probabilità della v.c. Binomiale è:
Essendo π = 0,2 abbiamo:
a)
b)
c)
0
p9 q0,2 0,8 9
2
p9: q0,2: 0,8 ?
)K2
1 • 0
d)
e)
)[2
0
1
2
p:: q0,2: 0,8 9?
Esercizio 3
r, }ru€
r, sr•r
1 — 1
vjwA
1
2
r, }stx
1,90 [ ) [ 2,00
b)
•
B
1,90 [ ) [ 2,10
r, x•€€
) [ 1,90
9,. P:,
[1[
, @
9,. P:,
B
) K 2,10
, @
:,
[1[
B1 [
C
P:,
, @
:,9 P:,
9,. P:,
, @
, @
1K2
1 0,9544 r, rۥt
d) 10000*0,0456=45,6 ovvero circa 46 bottiglie
c)
pONq= N 1
=
OPN
•0,1074 0,2684—r, t•€•
10
L M 0,29 0,8 . 0,2684
1
0,1074 0,2684 0,3020 r, tuu~
La funzione di densità della v.c. normale è œ )
a)
)
A
R√:S
9
C
P
!#T U
UVU
2[1[0
1K
r, €uu•
2[1[2
:,9 P:,
, @
r, €uu• ∗
C
1[
2
Esercizio 4
Si tratta di un confronto tra le medie di tre campioni.
Il sistema d’ipotesi è
6 : 29 2: μ
5
69 : z¥„A+jvŽA„AvƒAGj+jvƒwAdGA
E’ un problema che si risolve attraverso l’ANALISI DELLA VARIANZA.
Preliminarmente calcoliamo le quantità seguenti:
)̅9
c9:
+9
6
∑ )9*>
+9
6,07
∑ )9* )̅9
†
+9
:
2,717
)̅:
c::
+:
6
∑ ):*>
+:
2,07
∑ ):* )̅:
†
+:
:
0,43
)̅
c:
+
∑ ) *>
+
∑ )
†
6
*
+
3,73
)̅
:
2,01
41
Successivamente esponiamo i calcoli per il calcolo della ANOVA
Natura della
variabilità
Devianza
Gradi di libertà
Varianze
Tra le classi
Entro le
classi
Totale
48,46
25,75
2
15
24,23
1,72
74,21
17
25,95
F
24,23:1,72 =
14,09
Il risultato del test (14,09) deve essere confrontato con la v.c. F di Snedecor/Fisher in
corrispondenza di 2 e 15 g.d.l. a livello di significatività del 5%. Il valore teorico è 3,68.
Il risultato del test cade nella zona di rifiuto che ci porta a concludere che
a) vi è una differenza significativa tra le vendite medie del prodotto ai diversi livelli di fattori;
b) la scelta di locazione che sembra differire significativamente è la posizione frontale;
c) il direttore dovrebbe privilegiare il posizionamento centrale del prodotto.
Esercizio 5
n = 9 numerosità del campione;
x = 200 media campionaria,
s = 12,92 scarto quadratico medio campionario,
t0,02; 8 = 2,896 t con 8 gradi di libertà.
L’intervallo richiesto è

s
s 
Pr  x − tα , n−1
≤ µ ≤ x + tα , n −1
 = 1−α
2
2
n
n


12,92
12,92 
Pr 200 − 2,896
≤ µ ≤ 200 + 2,896
 = 0,98 ≈ {187;213}
9
9 

42
SIMULAZIONE X
1) Una scatola contiene 10 palline rosse, 30 bianche, 20 gialle e 15 color arancio. Se si
estraggono successivamente due palline, calcolare la probabilità che:
a) Entrambe le palline siano bianche nel caso di estrazione con ripetizione;
b) Entrambe le palline siano rosse nel caso di estrazione senza ripetizione;
c) La prima sia rossa e la seconda bianca nel caso di estrazione senza ripetizione;
d) Al massimo una sia rossa;
e) Almeno una sia gialla nel caso di estrazione con ripetizione.
2) Assumendo che il numero di errori che si verificano in un giorno in una rete locale (LAN)
sia distribuito secondo la legge di Poisson e che il numero medio di errori in un giorno sia
pari a 2,4 calcolate la probabilità che in un giorno:
a) Non si verifichino errori;
b) Che si verifichi esattamente un errore;
c) Che riscontrino almeno due errori;
d) Si verifichino non più di tre errori;
e) Calcolare la varianza di detta distribuzione.
3) La tabella seguente mostra il peso di un campione di studenti. Adattate una distribuzione
normale alla distribuzione data (calcolare le probabilità per ciascuna classe di peso,
utilizzando la funzione di densità normale).
Classi di peso
Studenti
Fino a 50
16
50 - 60
43
60 - 70
82
70 – 80
45
Oltre 80
15
4) In uno studio sulla combinazione tra lavoro e famiglia, sono state intervistate 500 donne con
elevato livello di istruzione che hanno abbandonato la carriera lavorativa per motivi
familiari. 330 donne intervistate hanno dichiarato di desiderare di tornare a lavorare.
Determinare un intervallo di confidenza al 95% per la proporzione di donne con
elevato grado di istruzione che hanno abbandonato la carriera per motivi familiari che
vogliono tornare a lavorare;
5) Una piccola pizzeria di quartiere nella sua pubblicità afferma che il tempo di consegna a
domicilio di una pizza (ad abitazioni del quartiere) è inferiore a quello di una importante
catena di pizze a domicilio.
Per verificare la validità dl messaggio pubblicitario si ordinano in momenti diversi
10 pizze dalla pizzeria di quartiere e 10 pizze dal punto di vendita della catena più vicino al
quartiere.
43
I tempi di consegna sono riportati nella tabella seguente:
Pizzeria
Catena
16.8
22.0
11.7
15.2
15.6
18.7
16.7
15.6
17.5
20.8
18.1
19.5
14.1
17.0
21.8
19.5
13.9
16.5
20.8
24.0
Fissato un livello di significatività α = 0,05, c’è evidenza che il tempo medio di
consegna è inferiore per la pizzeria di quartiere?
SOLUZIONI X
Esercizio 1
a) Pr
∩
b) Pr k ∩ k
c) Pr k ∩
∗ I@
I@
9
∗I
.
I@
9
∗I
I@
r, }t
:@
9?@
:
r, r}t
r, r•€
I
1
B
La funzione di probabilità della v.c. di Poisson è:
)
d) Pr z¥„zGGƒ„j1GƒzdjGGz
e) Pr z¥„A+j1GƒzŒƒz¥¥z
1
9
I@
∗
9
C
I@
Pr ® ∩ ® ∪ d ® ∩ ®̅ ∪ Pr ®̅ ∪ ®
dove Pr ® ∩ ®
∗
I@ I@
20 55
44
Pr ® ∩ ®̅
∗
75 75 225
55 20
44
Pr ®̅ ∩ ®
∗
75 75 225
:
Pr k ∩ k
:
9_
1
::@
9
::@
::@
r, x~
r, €t•
Esercizio 2
AP
!
N!
Essendo λ=2,4, abbiamo:
a)
0
A P:,
:, /
!
0,091
b)
1
A P:, 9! 0,218
c) P(x≥2) = 1- •Pr 0
Pr 1 — 1
!
:,
d) P(x≤3) = ∑NX A P:,
0,779
:,
0
`
N!
/
P
A
!
0,091
0,218
r, tx}
0,091+
44
1
2
AP
AP
`
9!
0,218+
U
:!
0,261+
3
AP
0,209=
!
e) Nella distribuzione di Poisson la media e la varianza sono uguali a λ; quindi la varianza è
uguale a 2,4.
›
Esercizio 3
La funzione di densità di probabilità della v.c. Normale è
Y
A
R√:S
9
!#T U
UVU
P
dove il parametro 2 è la media e il parametro σ2 è la varianza (σ è lo scarto quadratico medio)
della stessa v.c.
Per adattare la distribuzione data ad una normale, occorre preliminarmente calcolare media e
varianza della distribuzione data.
Classi di peso
Fino a 50
50 - 60
60 - 70
70 – 80
Oltre 80
3:
Studenti
16
43
82
45
15
∑ )*
2
+
2 : +*
Valore centrale
45
55
65
75
85
xi n i
720
2365
5330
3375
1275
∑OìX9 )* +*
+
65
21200
201
13065
201
105,5; 3
(xi-µ)2ni
6400
4300
0
4500
6000
Y105,5
10,3
A questo punto occorre calcolare le aree al di sotto della curva normale per ognuna
delle classi di statura che rappresentano le rispettive probabilità:
Pr
∞[
[ 50
\
Standardizzando, abbiamo
Pr B ∞ [ ; [
)
3
2
C
Pr L ∞ [ ; [
@
1
P^ 3√28
A
50 65
M
10,3
P
NP] U
:RU
Pr
∞[;[
1,46
Dalla tavola B troviamo che P(z=-1,46)=0,42786;
per cui la probabilità cercata è 0,5 – 0,42786= 0,07214.
45
Analogamente calcoliamo le altre probabilità:
)9
Pr B
2
3
[;[
):
Pr 50 [
3
2
C
Pr L
[ 60
\
_
@
1
3√28
A
P
NP] U
:RU
50 65
60 65
[;[
M
10,3
10,3
Pr
1,46 [ ; [
0,49
Dalla tavola B troviamo che P(z=-1,46)=0,42786; mentre P(z=-0,49)=0,18793
per cui la probabilità cercata è 0, 42786 – 0, 18793 = 0,23993.
)9
Pr B
3
2
):
[;[
Pr 60 [
3
2
C
[ 70
\
I
_
1
3√28
A
P
NP] U
:RU
60 65
70 65
Pr L
[;[
M
10,3
10,3
Pr
0,49 [ ; [ 0,49
Dalla tavola B troviamo che P(z=0,49)=0,18793*2 = 0,37586.
)9
Pr B
3
2
[;[
):
Pr 70 [
3
2
C
[ 80
\
?
I
1
3√28
A
P
NP] U
:RU
70 65
80 65
Pr ¯L
[;[
M°
10,3
10,3
Pr 0,49 [ ; [ 1,46
Dalla tavola B troviamo che P(z=0,49)=0,18793; mentre P(z=1,46)=0,42786
per cui la probabilità cercata è 0,42786 - 0,18793 = 0,23993.
)9
Pr B
3
2
Pr 80 [
[ ; [ ∞C
[∞
\
^
?
1
3√28
A
P
80 65
Pr L
[ ; [ ∞M
10,3
NP] U
:RU
Pr 1,70 [ ; [ ∞
Dalla tavola B troviamo che P(z=1,46)= 0,42786;
per cui la probabilità cercata è 0,5 – 0,42786 = 0,07214.
46
Nella tabella seguente, riportiamo i dati utili per l’esercizio
Classi di peso
Pr (X studenti)
Valori teorici
Valori osservati
Fino a 50
0,07214
14,5
16
50 - 60
0,23993
48,2
43
60 - 70
0,37586
75.5
82
70 – 80
0,23993
48,2
45
Oltre 80
0,07214
14,5
15
Da notare che l’adattamento della distribuzione Normale alla distribuzione data è piuttosto
buono.
Esercizio 4
Si tratta di determinare l’intervallo di confidenza della percentuale. La v.c. di
riferimento è la Binomiale, ma trattandosi di grande campione, per il teorema di DeMoivreLaplace, possiamo fare riferimento alla v.c. normale standardizzata.
L’intervallo di confidenza della percentuale per grandi campioni è:
1
g
Pr …=
1e>: †
= 1
+
=
1e>: †
[8[=
= 1
+
=
‡
P = 330/500 = 0,66
Pr …0,66
1,96†
0,66 1 0,66
[ 8 [ 0,66
500
1,96†
d 0,62 [ 8 [ 0,70
0,66 1 0,66
‡
500
0,95
0,95
Con una probabilità pari al 95% l’intervallo precedente potrebbe essere uno di quelli
che contiene la percentuale incognita.
Esercizio 5
Il sistema d’ipotesi è 5
6 ∶ 29 2:
69 ∶ 29 E 2:
Calcoliamo preliminarmente le medie e le varianze campionarie:
)̅9
)̅ :
O`
∑ìX9
)9*
+9
U
∑OìX9
):*
+:
167
10
188,8
10
16,7G9:
18,9G::
∑ )9*
+9
∑ ):*
+:
)̅9
1
:
)̅ :
1
9,58
:
8,22
47
Prima di effettuare il test sulle medie occorre stimare la varianza comune attraverso
la media ponderata delle due varianze dei campioni:
c
:
c9: +9
1
+9
c:: +:
+: 2
1
9,58 9
18
8,22 9
8,9
Trattandosi di piccoli campioni, la statistica test da adottare per verificare l’ipotesi è
F
9
1
G<
+9
:
1
+:
16,7
18,9
1
2,98<
10
1
10
1,65
Dalla tavola della T di Student, in corrispondenza di 18 gradi di libertà e di α=0,10
(ipotesi alternativa unidirezionale sinistra), troviamo t=-1,734.
Il valore del test è maggiore del valore soglia per cui dobbiamo concludere che non c’è
evidenza empirica sufficiente per rifiutare l’ipotesi nulla. Sulla base di questo risultato,
possiamo dire che la pizzeria di quartiere non ha sufficienti prove a sostegno del suo messaggio
pubblicitario.
48
SIMULAZIONE XI
1. Sul banco di un supermercato ci sono 45 confezioni di latte, delle quali 25 scadono oggi e
20 domani.
a. Si calcoli la probabilità che 2 confezioni estratte senza reinserimento abbiano la stessa data
di scadenza.
b. Supponendo di aver estratto 2 confezioni con data di scadenza differente e di aver rimesso
sul banco la confezione che scade oggi, si calcoli la probabilità che una confezione scelta a
caso scada domani.
2. La quantità di liquido contenuta nelle bottiglie prodotte da un’azienda che produce
bevande analcoliche si distribuisce come una normale con µ = 2 litri e σ = 0,05 litri. Se si
estrae a caso una bottiglia, qual è la probabilità che quantità di liquido contenuta:
a) Sia compresa tra 1,90 e 2,10 litri?
b) Sia inferiore a 1,85 litri?
c) Sia non superiore a 2,05 litri?
d) Determinare il contenuto in litri superato dal 90% delle bottiglie;
e) Determinare l’intervallo centrato intorno alla media 2 litri, in cui cadono l’98% delle
bottiglie.
3. Il manager che si occupa del controllo di qualità in un’azienda produttrice di lampadine
intende stimare la durata media di un grande carico di lampadine. Si sa che lo scarto
quadratico medio della durata delle lampadine è di 100 ore. Si estrae un campione di 64
lampadine e la media campionaria risulta pari a 350 ore.
a) Calcolate un intervallo di confidenza al 95% per la vera durata media delle lampadine
del carico;
b) E’ necessario supporre che la durata delle lampadine abbia distribuzione normale?
Spiegate.
c) Pensate che il produttore possa affermare che le lampadine durano in media 400 ore?
Spiegate.
4. Una piccola pizzeria di quartiere nella sua pubblicità afferma che il tempo di consegna a
domicilio di una pizza (ad abitazioni del quartiere) è inferiore a quello di una importante
catena di pizze a domicilio.
Per verificare la validità dl messaggio pubblicitario si ordinano in momenti diversi
10 pizze dalla pizzeria di quartiere e 10 pizze dal punto di vendita della catena più vicino al
quartiere.
I tempi di consegna sono riportati nella tabella seguente:
Catena
Pizzeria
28,8
22.0
11,7
15.2
15,6
18.7
16,7
15.6
17,5
20.8
18,1
19.5
14,1
17.0
21,8
19.5
13,9
16.5
20,8
24.0
49
Fissato un livello di significatività α = 0,05, c’è evidenza che il tempo medio di
consegna è inferiore per la pizzeria di quartiere?
5. Un campione di 500 soggetti abitanti in un’area metropolitana viene sottoposto ad un
sondaggio in termini di consumo. Una delle domande è la seguente: “Ti piace fare
shopping per acquistare capi di abbigliamento?” Rispondono positivamente 136 uomini su
240 e 224 donne su 260.
c) E’ possibile affermare ad un livello di significatività pari a 0,01 che esiste una differenza
significativa tra le proporzioni di uomini e donne a cui piace fare shopping?
d) Calcolate il p-value e interpretatene il risultato.
SOLUZIONI XI
Esercizio 1
Si indichi con Oi l’evento “la i-esima confezione estratta scade oggi” e con. Di l’evento “la iesima confezione estratta scade domani” (i=1,2).
a) La probabilità che le due confezioni estratte abbiano la medesima scadenza è data dalla
somma
P(O1∩O2)+P(D1∩D2)=49/99, essendo
P(O1∩O2)=P(O2|O1)P(O1)=(24/44)(25/45)=10/33
e
analogamente
P(D1∩D2)=P(D2|D1)P(D1)=(19/44)(20/45)=19/99.
b) Estratta una confezione che scade domani, la probabilità che una seconda confezione scelta
a caso scada domani è pari a P(D2|D1) = P(D2∩D1)/ P(D1) = (19/44)(20/45)(45/20) =
19/44 Essendo P(D1) = 20/45. Si noti che avendo già estratto una scatola che scade
domani ne rimangono 44 sul banco di cui 19 ancora con scadenza domani. Il risultato si può
quindi ottenere come rapporto fra casi favorevoli e possibili nella nuova situazione che si
origina dopo che una scatola con scadenza domani è stata rimossa dal banco
Esercizio 2
La funzione di densità di probabilità della v.c. Normale è
NP] U
1
P
Y
A :RU 3√28
Per la distribuzione della quantità contenuta nelle bottiglie la media e lo scarto
quadratico medio sono rispettivamente:
μ 2; σ 0,05
A questo punto occorre calcolare le rispettive probabilità:
a) Pr 1,90 [
[ 2,10 Standardizzando, abbiamo:
1,90 2,00
2,10 2,00
Pr L
[;[
M
0,05
0,05
Pr
2[;[
2
Dalla tavola B troviamo che P(z=2)=0,4772;
per cui la probabilità cercata è 0,4772x2 = 0,9544.
50
b) Analogamente calcoliamo le altre probabilità: Pr
Pr L; [
1,85 2,00
M
0,05
[ 1,85
Pr Z [
3
Dalla tavola B troviamo che P(z=-3)=0,49865;
per cui la probabilità cercata è 0,5 - 0, 49865 = 0,00135
c) Pr
[ 2,05
Pr L; [
2,05 2,00
M
0,05
Pr Z [ 1
Dalla tavola B troviamo che P(z=1)=0,3413;
per cui la probabilità cercata è 0,5 + 0,3413 = 0,8413;
d)
e)
d
K)
0,90
Dalla tavola B troviamo che P(z)=0,40 quando Z = 1,285; per cui:
2 13 2 1,285 ∗ 0,05 }, xst
d )9 [ [ ):
0,98
Dalla tavola B troviamo che P(z)=0,44 quando Z = 1,555; per cui:
)9
):
2
2
13
13
2
2
1,555 ∗ 0,05
1,555 ∗ 0,05
}, x••
•, ru~
Esercizio 3
Trattasi di
L’intervallo è
a)
d £)̅
1e>:
costruzione dell’intervallo di confidenza della media con varianza nota.
[ 2 [ )̅
O
R
√
d 5350
1e>: O¤ 0,95
√
100
1,96
[ 2 [ 350
√64
R
dh325,5 [ 2 [ 374,5i
1,96
100
√64
0,95
f
0,95
51
b) No. Essendo σ noto e n=64 (grande campione), per il teorema del limite centrale, la
distribuzione di è approssimativamente normale;
c) Non si può affermare che le lampadine durano in media 400 ore. Sulla base dei dati
campionari, un valore di 400 ore supera la media campionaria osservata, 350 ore, di 4 volte
lo scarto quadratico medio.
Esercizio 4
Il sistema d’ipotesi è 5
6 ∶ 29 2:
69 ∶ 29 E 2:
Calcoliamo preliminarmente le medie e le varianze campionarie:
)̅9
)̅ :
O`
∑ìX9
)9*
+9
179
10
U
∑OìX9
):*
+:
188,8
10
17,9G9:
18,9G::
∑ )9*
+9
∑ ):*
+:
)̅9
1
:
)̅ :
1
24,25
:
8,22
Prima di effettuare il test sulle medie occorre stimare la varianza comune attraverso
la media ponderata delle due varianze dei campioni:
c:
c9: +9
1
+9
c:: +:
+: 2
1
22,63 9
18
8,22 9
16,23
Trattandosi di piccoli campioni, la statistica test da adottare per verificare l’ipotesi è
F
9
1
G<+
9
:
1
+:
17,9
18,9
1
3,94<10
1
10
0,54
Dalla tavola della T di Student, in corrispondenza di 18 gradi di libertà e di α=0,10
(ipotesi alternativa unidirezionale sinistra), troviamo t=-1,734.
Il valore del test è minore del valore soglia per cui dobbiamo concludere che non c’è
evidenza empirica sufficiente per rifiutare l’ipotesi nulla. Sulla base di questo risultato,
possiamo dire che la pizzeria di quartiere non ha sufficienti prove a sostegno del suo messaggio
pubblicitario.
52
Esercizio 5
a) Si tratta della verifica d’ipotesi del valore di una percentuale.
Il sistema d’ipotesi è
6 : 89
5
69 : 89
Il test è
;
dove
e
=9
Abbiamo, quindi:
;
=
<= 1
136
240
9
+9
8:
8:
=9
=:
1
= B
+9
0,567=:
:
+:
0,567
136
240
0,862
1
C
+:
224
260
224
260
0,862
0,72
7,34
1
1
<0,72 1 0,72 B
240 260C
Quindi l’ipotesi nulla deve essere rifiutata in quanto il valore empirico (-7,34) è
notevolmente inferiore al valore soglia di sinistra (-2,58): esiste una differenza significativa
fra le proporzioni di uomini e donne che amano fare shopping.
b) Il p-value è prossimo a zero e di conseguenza la decisione assunta comporta un rischio di
errore quasi nullo.
53
ALTRE SIMULAZIONI SENZA SOLUZIONI
SIMULAZIONE XII
1) Nella tabella seguente sono riportate le risposte di 200 studenti universitari ad un sondaggio
che ha come oggetto la diffusione di carte di credito e di bancomat.
Carte di
Bancomat
credito
Sì
No
Sì
60
60
No
15
65
a) Sapendo che uno studente possiede una carta di credito, qual è la probabilità che sia in
possesso anche di bancomat?
b) Sapendo che uno studente non possiede un bancomat, qual è la probabilità che sia in
possesso di una carte di credito?
c) I due eventi sono indipendenti?
2) Supponete che il manager della divisione servizi alla clientela di una società di prodotti
elettronici intenda stabilire se i clienti che hanno effettuato almeno un acquisto negli ultimi
12 mesi sono soddisfatti del prodotto. Il manager programma di intervistare questi clienti,
contattandoli sulla base dei certificati di garanzia spediti dopo l’acquisto. Si valuta che il
20% dei clienti non è completamente soddisfatto del prodotto. Supponiamo che si estragga
un campione casuale di 400 clienti, qual è la probabilità che la proporzione campionaria di
clienti che non sono completamente soddisfatti sia:
a) Compresa tra il 16% e il 24%;
b) Compresa tra il 18% e il 22%;
c) Compresa tra il 14% e il 26%;
d) Superiore al 25%. Teorema di De Moivre Laplace
3) Il manager di una filiale di una catena di abbigliamento sportivo intende stimare i gusti dei
clienti del suo negozio. A tale scopo decide di prendere in considerazione due variabili:
l’ammontare di denaro speso dai clienti e se i clienti sono interessati all’acquisto di scarpe
sportive. I risultati di un’indagine condotta su 70 clienti sono i seguenti:
• Ammontare speso: )̅ 28,52AŽdj, c 11,39AŽdj
• 28 clienti si dichiarano interessati all’acquisto di scarpe sportive.
a) Costruite un intervallo di confidenza al 95% per stimare l’ammontare della spesa media
dell’abbigliamento sportivo;
b) Costruite un intervallo di confidenza al 90% per stimare la proporzione dei clienti
interessati all’acquisto di scarpe sportive.
4) Un’azienda manifatturiera produce isolatori elettrici. Se un isolante si rompe mentre è in uso
è molto probabile che si verifichi un corto circuito. Per verificare la forza degli isolatori
prodotti si decide di procedere ad un test distruttivo: la forza viene misurata valutano il peso
necessario a rompere un isolatore (misurato in Kg.). Di seguito sono riportati 30 dati
osservati durante questo tipo di esperimenti:
1,870
1,784
1,866
1,820
1,764
1,744
1,728
1,522
1,734
1,550
1,788
1,680
1,656
1,696
1,662
1,756
1,688
1,810
1,610
1,592
1,734
1,762
1,810
1,652
1,634
1,662
1,774
1,866
1,752
1,736
54
a) Si può concludere, ad un livello di significatività pari a 0,05 che la forza media di un
isolatore sia superiore a 1,500 Kg;
b) Quali ipotesi devono essere soddisfatte per condurre il test del punto a)?
c) Calcolate il p-value e interpretatene il significato.
5) Il consumo di benzina di un’auto è una delle caratteristiche che gli automobilisti valutano
quando devono scegliere un auto? In un’indagine questa domanda è stata posta a uomini e
donne che dovevano acquistare una nuova auto. Nell’indagine sono solo riportate le
percentuali campionarie osservate e non sono fornite indicazioni sulle ampiezze
campionarie:
Tiene conto
Sesso
del consumo
M
F
Sì
76%
84%
No
24%
16%
a) Supponiamo che i due campioni abbiano entrambi ampiezza pari a 50. E’ possibile
affermare ad un livello di significatività pari a 0,05 che esiste una differenza
significativa tra le proporzioni di maschi e femmine che tengono conto del consumo
quando valutano un auto da acquistare? Calcolate il p-value e interpretatene il
significato.
b) Supponiamo che i due campioni abbiano entrambi ampiezza pari a 500. E’ possibile
affermare ad un livello di significatività pari a 0,05 che esiste una differenza
significativa tra le proporzioni di maschi e femmine che tengono conto del consumo
quando valutano un auto da acquistare? Calcolate il p-value e interpretatene il
significato.
c)
Discutete l’effetto dell’ampiezza campionaria sui risultati dei punti a) e b).
55
SIMULAZIONE XIII
1) Il ministero dei trasporti raccoglie i dati relativi al numero di bagagli danneggiati. In
particolare, nel 2010, una compagnia aerea ha un tasso di 3.21 bagagli danneggiati per 1000
passeggeri. Qual è la probabilità che per i prossimi 1000 passeggeri la compagnia aerea
restituisca:
a) Nessun bagaglio danneggiato?
b) Almeno un bagaglio danneggiato?
c) Almeno due bagagli danneggiati?
d) Non più di tre bagagli danneggiati?
e) Qual è la media e la varianza della v.c. utilizzata?
2) Le commissioni pagate alle agenzie di viaggio da parte delle compagnie aeree hanno
continuato a diminuire per molti anni. Per aumentare i profitti le agenzie di viaggio
applicano ora una tassa sui biglietti aerei emessi, solitamente compresa tra i 10 e 25 euro. In
uno studio condotto dall’associazione degli agenti di viaggio si sostiene che la percentuale
di agenzie che ha adottato questa strategia è intorno al 90%. Estratte casualmente 10
agenzie, calcolare la probabilità:
a) Nessuna applichi una tassa sui biglietti emessi;
b) Esattamente una applichi una tassa sui biglietti emessi;
c) Al massimo due applichino una tassa sui biglietti emessi;
d) Almeno tre applichino una tassa sui biglietti emessi;
e) Calcolare la media e la varianza.
3) Il tempo impiegato nella sessione di utilizzo della posta elettronica ha una distribuzione
normale con media 8 minuti e scarto quadratico medio 2 minuti. Si estrae un campione di 25
sessioni.
a) Calcolate 3N̅
b) Qual è la probabilità che una media campionaria sia compresa tra 7.8 e 8.2 minuti?
c) Qual è la probabilità che una media campionaria sia compresa tra 7.5 e 8.0 minuti?
d) Qual è la probabilità che una media campionaria sia compresa tra 8.5 e 9.0 minuti?
e) Qual è la probabilità che una media campionaria sia maggiore di 9, 5 minuti?
4) Il responsabile dell’area informatica di una grande società vuole confrontare l’utilizzo
informatico in due settori della società: il settore contabilità e il settore ricerca. A tal fine
vengono estratti 5 progetti realizzati nell’ultima settimana nel primo settore e 6 progetti
realizzati nell’ultima settimana nel secondo settore, e si rileva per ciascun progetto il tempo
di elaborazione (in secondi) richiesto dal calcolatore:
Settore
Tempo di elaborazione (in secondi)
Contabilità
9
3
8
7
12
Ricerca
4
13
10
9
9
6
a) Si può affermare che il tempo medio di elaborazione nel reparto ricerca è superiore a 6
secondi ad un livello di significatività del 5%?
b) Si può affermare che il tempo medio di elaborazione nel reparto contabilità è superiore a
6 secondi ad un livello di significatività del 5%?
56
c) I dati evidenziano l’esistenza di una differenza tra i tempi medi di elaborazione per
progetti dei due settori ad un livello di significatività del 5%?
d) Calcolate il p-value dei test precedenti e interpretatene il significato.
5) Sempre più donne rinunciano alla maternità per i limiti di tempo imposti dalle proprie
carriere. Tuttavia, molte donne tentano di combinare famiglia e lavoro. Tra le 187
partecipanti al congresso del 2010 delle donne più potenti del mondo degli affari intervistate
a riguardo, 133 hanno dichiarato di avere almeno un figlio. Supponiamo che quello
considerato sia un campione casuale estratto dalla popolazione delle donne di successo.
a) Qual è la proporzione campionaria di donne di successo che hanno figli?
b) Si può affermare, con un livello di significatività pari a 0.05, che più della metà delle
donne di successo hanno figli?
c) Si può affermare, con un livello di significatività pari a 0.05, che più di 2/3 delle donne
di successo hanno figli
d) Calcolate il p-value dei test precedenti e interpretatene il significato.
57
SIMULAZIONE XIV
1) E’ stata condotta una indagine per valutare se le aziende di grandi dimensioni sono meno
propense delle aziende di medie-piccole dimensioni ad offrire azioni ai membri del proprio
consiglio di amministrazione. I risultati campionari sono i seguenti:
su 189 aziende di grandi dimensioni, 40 offrono le proprie azioni ai membri del consiglio di
amministrazione; su 180 aziende di medie-piccole dimensioni, 43 offrono le proprie azioni
ai membri del consiglio di amministrazione. Dopo aver costruito la distribuzione doppia,
calcolare qual è la probabilità che una azienda scelta a caso:
a) Offra azioni ai membri del consiglio di amministrazione;
b) Sia di dimensioni medie-piccole dimensioni e non offra azioni ai membri del consiglio
di amministrazione;
c) Sia di dimensioni medie-piccole dimensioni oppure offra azioni ai membri del consiglio
di amministrazione;
d) Spiegare la differenza tra il punto b) e il punto c).
2) Il numero di volte che un sistema si interrompe nell’arco di un mese segue una distribuzione
di Poisson. Ci si aspetta che in un mese il sistema si interrompa 2,5 volte. Qual è la
probabilità che in un certo mese il sistema:
a) Non si interrompa;
b) Si interrompa almeno una volta;
c) Si interrompa non più di tre volte;
d) Ci interrompa esattamente tre volte.
3) Un processo produttivo produce bulloni che devono essere montati su particolari strutture.
Una particolare struttura richiede bulloni con un diametro di 22 mm.; tuttavia i bulloni sono
accettabili (possono essere montati) purché il loro diametro sia compreso tra 21.9 e 22.01
mm. Il processo produttivo genera bulloni il cui diametro si può assumere distribuito
normalmente, con valore atteso 22 mm. e scarto quadratico medio 0,05 mm.
a) Qual è la probabilità che venga prodotto un bullone con diametro compreso tra 21.9 e 22
mm?
b) Qual è la probabilità che venga prodotto un bullone accettabile?
c) Solo il 2% dei bulloni prodotti ha un diametro superiore a …?
d) Solo il 3% dei bulloni prodotti ha un diametro inferiore a …?
4) Si vogliono studiare le caratteristiche delle villette monofamiliare situate in una certa zona
residenziale. Su un campione casuale di 70 case vengono rilevati i seguenti dati:
175,9; c 38
• Superficie della casa riscaldata:
• 42 case hanno un impianto di condizionamento.
a) Costruire un intervallo di confidenza al 99% per la superficie media riscaldata nella
popolazione delle villette monofamiliare;
b) Costruire un intervallo di confidenza al 95% per la proporzione di villette
monofamiliare con impianto di riscaldamento nella popolazione;
5) Con riferimento a molti processi industriali si utilizza il termine “work in progress (WIP)”.
Negli impianti di fabbricazione di libri il WIP rappresenta il tempo necessario per piegare,
riunire, cucire e rilegare i fogli che provengono dalla stessa pressa. I dati che seguono sono
relativi al tempo di lavorazione (tempo in giorni che intercorre tra quando i libri vengono
stampati a quando sono impacchettati nei cartoni) per due campioni di 20 libri estratti da due
impianti di fabbricazione.
58
5,62
11,62
5,29
7,29
16,25
7,50
10,92
7,96
9,54
11,46
16,62
12,62
5,75
12,46
9,17
13,21
Confrontare le differenze tra i
l’interpretazione del p-value.
Impianti A
11,46
21,62
8,45
4,42
10,50
7,58
Impianto B
25,75
15,41
14,29
6,00
2,33
14,25
tempi di lavorazione per i
8,58
9,29
5,41
7,54
11,42
8,92
13,13
13,71
10,04
5,37
6,25
9,71
due impianti attraverso
59
SIMULAZIONE XV
1) Consideriamo un’indagine condotta su 168 investitori, ai quali è stato chiesto se hanno
investito in fondi comuni d’investimento e se hanno guadagnato.
Hai guadagnato?
Hai investito in fondi comuni d’investimento?
Si
No
Totale
Si
18
94
112
No
11
45
56
Totale
29
139
168
Consideriamo 10 investitori scelti a caso.
a) Qual è la probabilità che più della metà siano investitori di fondi comuni;
b) Qual è la probabilità che più della metà abbiano guadagnato;
c) Qual è la probabilità che più della metà siano investitori di fondi comuni e abbiano
guadagnato?
d) Come cambiano queste probabilità se estraiamo 20 investitori?
2) Una società di trasporti ha stabilito, sulla base dell’esperienza di un anno, che la distanza
percorsa da ciascun autocarro ha distribuzione normale caratterizzata da µ = 50.000 km. e σ
= 12.000 km. Scegliendo a caso un autocarro:
a) Qual è la probabilità che percorra tra 35.000 e 45.000 km?
b) Qual è la probabilità che percorra più di 45.000 km?
c) Qual è la probabilità che percorra meno di 60.000 km?
Se si estrae un campione di 16 autocarri:
d) Qual è la probabilità che la distanza media percorsa sia inferiore a 45.000 km.?
e) Qual è la probabilità che la distanza media percorsa sia compresa tra 44.000 e 48.000
km?
3) Un revisore dei conti di una compagnia che si occupa delle assicurazioni intende stabilire la
proporzione di richieste di risarcimento che vengono pagate dal ramo sulla salute entro due
mesi dalla ricezione della richiesta. Viene estratto un campione casuale di 200 richieste e si
osserva che 80 di queste sono pagate entro due mesi dalla richiesta.
A9 calcolate un intervallo di confidenza al 99% per la proporzione di richieste pagate entro
due mesi nella popolazione
Se si ritiene che il 90% delle richieste debba essere pagato entro due mesi, cosa dovrebbe
riferire il revisore dei conti alla direzione sulla performance del ramo di assicurazioni
considerato?
4) Il responsabile del processo di formazione di una società che produce componenti elettronici
vuole confrontare i risultati di due differenti metodi di addestramento degli addetti, uno
basato sulla formazione individuale e uno che si basa sulla formazione di gruppo. Estratti a
caso 80 addetti della società, questi vengono ripartiti in due gruppi di 40 componenti
ciascuno: I primi usufruiscono della formazione individuale ed hanno impiegato un tempo
medio di 47 minuti con uno scarto quadratico medio di 8 minuti; i secondi della formazione
di gruppo ed hanno impiegato un tempo medio di 53 minuti con uno scarto quadratico medio
di 10 minuti.
a) Assumendo varianze uguali, si può affermare che esiste una differenza tra i tempi medi
di assemblaggio per gli addetti formati secondo i due diversi sistemi descritti?
b) Calcolare il p-value e interpretarne il significato.
60
5) E’ stato condotto uno studio relativo al ruolo dei media nella vita di un bambino. In una
domanda dell’indagine si chiedeva ai bambini se usassero o meno il computer tutti i giorni.
Su 1090 bambini con età compresa tra i2 e i 7 anni, 283 hanno risposto in maniera
affermativa. Su 2065 ragazzini con età compresa tra gli 8 e i 18 anni, sono stati 1053 a
rispondere affermativamente.
a) E’ possibile affermare ad un livello di significatività pari a 0,05 che esiste una differenza
significativa tra le proporzioni dei bambini che usano giornalmente il computer nei due
gruppi di età?
b) Calcolate il p-value e interpretatene il significato.
61