Numeri Complessi

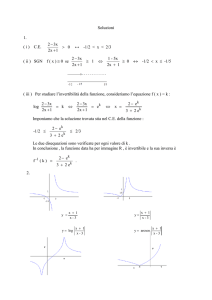
Parte II
Numeri Complessi
34
4
Incontro del 22 gennaio
2013
4.1
Numeri immaginari
Già gli antichi greci (Erone∗ , I secolo a.c.) utilizzarono nei loro trattati radici
quadrate di numeri negativi. Molte altre volte nella storia ci si imbattè nel dover
risolvere equazioni di secondo grado con discriminante negativo, ad esempio
x2 + 1 = 0, che ammette come soluzione l’unità immaginaria
√
i = −1
e il numero ad essa opposto −i. L’esigenza di introdurre questo nuovo tipo di
numeri potrebbe sembrare artificiosa ed essere liquidata assumendo che l’equazione x2 + 1 = 0 non abbia alcuna radice. Nel XVI secolo il matematico italiano
Niccolò Fontana detto il Tartaglia† trovò un metodo algebrico per risolvere le
equazioni di terzo grado. Egli mostrò che tali equazioni possono essere sempre
ricondotte, con un cambio di variabile, a equazioni aventi la forma particolare
x3 + px + q = 0.
(4.1)
La soluzione della (4.1) sembra che fosse già nota in precedenza al matematico
Scipione Del Ferro‡ e al suo allievo Antonio Maria Fior, detto Floridus in latino.
Essi però non conoscevano la soluzione del caso generale.
∗ Erone
di Alessandria (chiamato anche Erone il Vecchio) è stato un matematico, ingegnere
e inventore greco antico.
Realizzò l’eolipila e molti altri congegni meccanici. È anche noto
p
per la formula A = p(p − a)(p − b)(p − c) che permette di esprimere l’area di un triangolo
a partire dalle lunghezze dei suoi lati a, b e c e dal suo semiperimetro p.
† Niccolò Tartaglia, soprannome di Niccolò Fontana (Brescia, 1499 circa – Venezia, 13
dicembre 1557), è stato un matematico italiano, il cui nome legato al noto triangolo.
‡ Scipione del Ferro (Bologna, 6 febbraio 1465 – Bologna, 5 novembre 1526) è stato un
matematico italiano, a cui si deve il primo metodo risolutivo per le equazioni di terzo grado.
35
La (4.1) si risolve ponendo x = u + v, dove le variabili u e v sono legate dalla
relazione 3uv = −p, ed inserendo tale sostituzione nella (4.1). Si ottiene
0 = x3 + px + q
= u3 + 3u2 v + 3uv 2 + v 3 + p(u + v) + q
= u3 + 3uv(u + v) + v 3 + p(u + v) + q =
= u3 − p(u + v) + v 3 + p(u + v) + q =
= u3 + v 3 + q
A questo punto si possono ricavare il valori di u3 e v 3 risolvendo il sistema
simmetrico

u3 + v 3 = −q
3
u3 · v 3 = − p
27
Cosicché i valori di u3 e v 3 sono le radici dell’equazione di secondo grado (in t)
t2 + qt −
ossia
q
u =− +
2
ottenendo infine
s
3
x=
3
r
p3
q2
+
4
27
q
− +
2
r
2
p3
=0
27
e
3
q
p
+
+
4
27
q
v =− −
2
3
s
3
q
− −
2
r
r
p3
q2
+
.
4
27
q2
p3
+
4
27
Questo metodo pone peró problemi anche per casi relativamente semplici. Se
consideriamo ad esempio l’equazione x3 − x = 0, che ammette le tre radici reali
2
3
0, 1 e −1, notiamo che per essa l’espressione q4 + p27 , che nelle formule risolutive
1
è posta sotto il segno di radice quadrata, è uguale a − 27
: un numero negativo.
Nonostante l’equazione ammetta tre radici reali, non è possibile risolverla con
metodi algebrici senza estendere il campo numerico ed introducendo i numeri
complessi.
4.2
Numeri complessi
Un numero complesso z è un’espressione della forma z = a + ib, dove a e b sono
due numeri reali
√ chiamati parte reale e parte immaginaria del numero complesso
z e dove i = −1 rappresenta l’unità immaginaria. Scriveremo allora Re(z) e
Im(z) per denotare rispettivamente le parti reale a e immaginaria b del numero
complesso z. La coppia di numeri reali (a, b) identifica univocamente il numero
complesso z. L’insieme dei numeri complessi viene denotato usualmente con il
simbolo C = {a + ib | a, b ∈ R}.
36
y
(a, b) = (ρ cos θ, ρ sen θ)
θ
b
+i 2
a
z =√ 2 + b
a
ρ=
x
O
Figura 4.1: Il numero complesso z come vettore
Il numero complesso z = a + ib può venire identificato con il punto di coordinate (a, b) del piano cartesiano ortogonale, oppure, ancora meglio, con il vettore
che spicca dall’origine√degli assi e termina nel punto (a, b).
La lunghezza ρ = a2 + b2 di tale vettore viene chiamata modulo del numero
complesso z e viene denotata con |z|. L’angolo θ, espresso in radianti, che
il vettore forma con il semiasse positivo delle ascisse è detto argomento di z
e viene denotato con arg(z). L’argomento di un numero complesso è
definito a meno di multipli interi dell’angolo giro 2π. Si vede facilmente
che a = |z| cos(arg(z)) = ρ cos θ e b = |z| sen(arg(z)) = ρ sen θ.
La somma due numeri complessi z = a+ib e w = c+id è il numero complesso
z + w = (a + c) + i(b + d), che corrisponde alla somma di z e w come vettori.
In particolare il numero complesso z = a + ib è somma di due vettori tra loro
y
(a + c, b + d)
z
w
w=
z+
w
(c, d)
c+
id
z
+
=a
ib
(a, b)
x
O
Figura 4.2: Somma di numeri complessi
perpendicolari: il vettore orizzontale a (che corrisponde al punto (a, 0) sull’asse
delle ascisse) e del vettore verticale ib (che corrisponde al punto (0, b) sull’asse
delle ordinate).
Per come è stata definita la somma di numeri complessi gode delle proprietà
associativa e commutativa, ammette 0 = 0 + i0 come elemento neutro ed ogni
37
numero complesso z = a + ib ha come opposto −z = −a + i(−b).
Dato un numero complesso z = a + ib è detto suo coniugato il numero
complesso z̄ = a − ib che ha parte immaginaria opposta rispetto a quella di z;
esso si ottiene riflettendo z rispetto all’asse delle ascisse. Chiaramente |z| = |z̄|
e arg(z̄) = − arg(z).
y
(a, b)
b
a
z=
+i
+θ
O
x
−θ
z̄ =
a−
ib
(a, −b)
Figura 4.3: Numero complesso coniugato
Il prodotto di numeri complessi si calcola imponendo che esso sia commutativo e distributivo rispetto alla somma e ricordando che i2 = −1:
(a + ib) · (c + id) = ac + aid + ibc + i2 bd =
= ac + i(ad + bc) + (−1)bd =
= (ac − bd) + i(ad + bc)
È facile verificare che il prodotto cosı̀ definito è associativo, commutativo, distributivo rispetto alla somma, ammette 1 = 1 + i · 0 come elemento neutro.
I numeri che hanno parte immaginaria nulla (appartengono all’asse delle
ascisse) sono individuati dalla loro parte reale. Si comportano rispetto a somma
e prodotto come numeri reali. Pertanto il numero complesso a = a + i · 0
coincide a tutti gli effetti con il numero reale a e l’asse delle ascisse viene in tal
modo identificato con l’insieme R. Pertanto l’insieme dei numeri reali R è un
sottoinsieme dell’insieme dei numeri complessi C che da quest’ultimo eredita le
operazioni di somma, prodotto e modulo (valore assoluto).
Una semplice verifica mostra che
z+w =z+w
z · w = z · w.
Dato un numero complesso z = a + ib si ha che
z · z̄ = (a + ib)(a − ib) = a2 − i2 b2 = a2 + b2 = |z|2 .
38
Pertanto, se z 6= 0, si trova che z ·
1
z̄
|z|2
= 1, cosicché l’inverso di z = a + ib
è il numero complesso
z −1 =
4.3
z̄
=
|z|2
a
a2 + b2
−i
b
a2 + b2
.
Forma polare o trigonometrica
Se denotiamo come sopra con ρ e θ rispettivamente il modulo e l’argomento di
z = a + ib, possiamo scrivere l’eguaglianza
z = ρ cos θ + iρ sen θ = ρ(cos θ + i sen θ)
che viene usualmente detta forma trigonometrica o polare del numero complesso
z. Il modulo ρ e l’argomento θ possono essere calcolati tramite le formule
p

ρ
=
a2 + b2




a

cos θ =
ρ




 sen θ = b
ρ
Il numero
cos θ + i sen θ viene denotato con eiθ = cos θ + i sen θ e ha modulo
√
2
|e | = cos θ + sen2 θ = 1. Rappresenta un numero complesso che giace sulla
circonferenza goniometrica (centrata nell’origine e di raggio unitario) e forma
con l’asse reale un angolo θ.
iθ
y
(a, b) = (ρ cos θ, ρ sen θ)
(cos θ, sen θ)
iθ
e
θ
O
x
1
Figura 4.4: Forma trigonometrica/polare del numero a + ib
39
4.4
Prodotti scalari e regola di De Moivre
Il prodotto scalare ~u ? ~v di due vettori ~u e ~v è definito come il prodotto del
modulo di ~u per la proiezione di ~v lungo ~u. Si vede immediatamente che
~u ? ~v = |~u| · |~v | · cos α,
dove α = ~uc~v è l’angolo formato dai due vettori.
y
~v
α
en
s
|~v |
α
O
~u
α
cos
|~v |
x
Figura 4.5: Prodotto scalare
È immediato verificare che il prodotto scalare è un’operazione commutativa
e distributiva rispetto alla somma di vettori:
~u ? (~v + w)
~ = ~u ? ~v + ~u ? w.
~
B
w
~ = −−→
BC
−−→
B
~v = O
B0
O
C
~v
~=
+w
−→
~u = OA
A
−−→
OC
Figura 4.6: Proprietà distributiva
40
C0
Riferendoci alla figura 4.4, abbiamo infatti che
−→ −−→
~u ? (~v + w)
~ = OA · OC 0 =
−→ −−→ −−−→
= OA · (OB 0 + B 0 C 0 ) =
−→ −−→ −→ −−−→
= OA · OB 0 + OA · B 0 C 0 ) =
= ~u ? ~v + ~u ? w,
~
dove tutti i prodotti denotati con un punto sono da intendersi tra misure
(eventualmente negative) di segmenti orientati.
Poichè i numeri complessi 1 = 1+0·i e i = 0+1·i sono tra loro perpendicolari
il loro prodotto scalare come vettori è nullo: 1 ? i = 0. Inoltre 1 e i hanno
entrambi modulo unitario. Possiamo allora calcolare il prodotto scalare dei due
numeri complessi z = a + ib e w = c + id ottenendo la seguente formula per il
prodotto scalare:
z ? w = (a + ib) ? (c + id) =
= a ? c + a ? id + ib ? c + ib ? id =
= a ? c + 0 + 0 + ib ? id
= ac + bd =
= Re(z) Re(w) + Im(z) Im(w)
Si trova allora
y
y
=
x
T(w) = d + ic
w = c + id
+η
π
−η
2
x
−η
w̄ = c − id
Figura 4.7: w e T(w)
41
ac − bd = z ? w̄
ad + bc = z ? T(w)
dove w̄ è il coniugato di w, mentre T(w) = d + ic = iw̄ è il numero complesso
che si ottiene riflettendo w rispetto alla prima bisettrice (ovvero scambiando tra
loro le sue coordinate). Si nota subito che l’angolo tra w̄ e T(w) è retto.
Scriviamo ora i numeri z e w in forma trigonometrica: z = ρz (cos θ + i sen θ)
e w = ρw (cos η + i sen η). L’angolo tra z e w̄ è uguale a θ + η mentre l’angolo
π
tra z e T(w) è uguale a − η − θ, pertanto si trova
2
ac − bd = z ? w̄ = |z||w| cos(θ + η) = ρz ρw cos(θ + η)
π
ad + bc = z ? T(w) = |z||w| cos
− η − θ = ρz ρw sen(θ + η)
2
da cui possiamo concludere che
z · w = (ac − bd) + i(ad + bc) = ρz ρw (cos(θ + η) + i sen(θ + η))
Regola di De Moivre. Il prodotto di due numeri complessi z e w aventi
rispettivamente moduli ρz e ρw e argomenti θ e η, è il numero complesso zw
avente modulo ρzw = ρz ρw uguale al prodotto dei moduli dei fattori e argomento
arg(zw) = arg(z) + arg(w) = θ + η uguale alla somma degli argomenti∗ .
In particolare si trova la formula
eiθ · eiη = (cos θ + i sen θ)(cos η + i sen η) = cos(θ + η) + i sen(θ + η) = ei(θ+η)
che mostra che la notazione esponenziale eiθ soddisfa formalmente le proprietà
delle potenze.
Esercizio. Dimostrare che il triangolo che ha per vertici i tre numeri complessi
1
u, v e w, ha area uguale a Im (u − w)(v − w) .
2
4.5
Formule di addizione degli archi per coseno
e seno
Dalla regola di de Moivre abbiamo
cos(α + β) + i sen(α + β) = ei(α+β) = eiα eiβ
= (cos α + i sen α)(cos β + i sen β) =
= (cos α cos β − sen α sen β) + i(sen α cos β + cos α sen β).
∗ Abraham
de Moivre (Vitry-le-François, 26 maggio 1667 – Londra, 27 novembre 1754) è
stato un matematico francese, amico di Isaac Newton. È noto per la formula di de Moivre
(che collega i numeri complessi con la trigonometria), i suoi lavori sulla distribuzione normale
e la teoria della probabilità, nonché scoprı̀ (anche se in forma incompleta) l’approssimazione
di Stirling.
42
Se ne ricavano le note formule di addizione degli archi
cos(α + β) = cos α cos β − sen α sen β,
sen(α + β) = sen α cos β + cos α sen β.
Esercizio. Trovare una formula per esprimere cos(nθ) come un polinomio Tn (x)
di grado n calcolato in cos θ.
Soluzione.
cos(nθ) + i sen(nθ) = einθ = (eiθ )n =
= (cos θ + i sen θ)n =
bn/2c X n
(−1)k (cos θ)n−2k (sin θ)2k +
=
2k
k=0
b(n−1)/2c X
+i
h=0
n
(−1)h (cos θ)n−2h−1 (sin θ)2h+1 .
2h + 1
Pertanto
bn/2c cos(nθ) =
X
k=0
bn/2c =
X
k=0
n
(−1)k (cos θ)n−2k (sin θ)2k =
2k
n
(−1)k (cos θ)n−2k (1 − cos2 θ)k =
2k
= Tn (cos θ).
dove
bn/2c Tn (x) =
X
k=0
n
(−1)k xn−2k (1 − x2 )k .
2k
I polinomi Tn (x) sono chiamati polinomi di Čebyšhëv ∗ e possono essere definiti
per ricorrenza tramite la formula
Tn+1 (x) = 2xTn (x) − Tn−1 (x).
Una proprietà interessante è Tn (x) ha sempre n radici reali distinte nell’intervallo [−1, 1].
∗ Pafnutij L’vovič Čebyšhëv (Borovsk, 16 maggio 1821 – San Pietroburgo, 8 dicembre 1894)
è stato un matematico e statistico russo. È considerato uno dei padri fondatori della grande
scuola matematica russa.
43
4.6
Formule di Eulero e formule di Werner
Dato un numero complesso z = a + ib notiamo che z + z̄ = a + ib + a − ib =
2a = 2 Re(z) e che z − z̄ = a + ib − a + ib = 2ib = 2i Im(z). Ne ricaviamo che
z + z̄
,
2
z − z̄
Im(z) =
.
2i
Re(z) =
Nel caso in cui z = eiθ si ha eiθ = cos θ + i sen θ = cos θ − i sen θ = cos(−θ) +
i(sen(−θ)) = e−iθ . Si hanno allora le formule di Eulero ∗ :
eiθ + e−iθ
,
2
eiθ − e−iθ
sen θ = Im(eiθ ) =
.
2i
cos θ = Re(eiθ ) =
Supponiamo di voler calcolare il prodotto cos α cos β, utilizzando le formule di
Eulero troviamo una delle formule di Werner† :
eiα + e−iα eiβ + e−iβ
·
2
2
ei(α+β) + ei(α−β) + ei(−α+β) + ei(−α−β)
=
=
4
2 Re(ei(α+β) ) + 2 Re(ei(α−β) )
=
=
4
1
= (cos(α + β) + cos(α − β))
2
cos α cos β =
Esercizio. Trovare in modo analogo tutte le altre formule di Werner.
Esercizio. Utilizzare le formule di Eulero per trovare le formule di prostaferesi.
Suggerimento. Notare che eiα +eiβ = ei(α+β)/2 (ei(α−β)/2 +ei(−α+β)/2 ) = . . .
4.7
Radici n-esime dell’unità
Un numero complesso w è detto radice n-esima dell’unità se wn = 1. Po2π
sto ξn = e n i = cos(2π/n) + i sen(2π/n) e dato un intero k troviamo che
k
ξn = cos(2kπ/n) + i sen(2kπ/n) è una radice n-esima dell’unità, infatti (ξnk )n =
∗ Leonhard Euler, noto in Italia come Eulero (Basilea, 15 aprile 1707 – San Pietroburgo,
18 settembre 1783), è stato un matematico e fisico svizzero. È considerato il più importante
matematico dell’Illuminismo. È noto per essere tra i più prolifici di tutti i tempi e ha fornito contributi storicamente cruciali in svariate aree: analisi infinitesimale, funzioni speciali,
meccanica razionale, meccanica celeste, teoria dei numeri, teoria dei grafi.
† Johann Werner (Norimberga, 14 febbraio 1468 – Norimberga, maggio 1522) è stato un
cartografo, matematico e religioso tedesco.
44
(ξnn )k = (e2πi )k = 1k = 1. Sappiamo però che le radici n-esime dell’unità sono al
più in numero di n, dal momento che il polinomio xn − 1 ha al massimo n radici
distinte e quindi il loro numero è in realtà esattamente uguale a n. Chiaramente
ξnk = ξnk+n da cui deduciamo che ξn0 , ξn , ξn2 , . . . , ξnn−1 sono tutte e sole le radici
n-esime di 1 e si dispongono sui vertici di un n-agono regolare inscritto nella
circonferenza goniometrica; uno dei vertici è il numero 1.
y
ξ72
ξ71
e 2iπ
iπ /7
/7
e4
ξ73
e 6iπ/
ξ70 = 1
e0
7
x
O
/7
e 10iπ/7
iπ
12
ξ74
e
/7
8iπ
e
ξ76
ξ75
Figura 4.8: Radici settime di 1
Esercizio. Una radice n-esima w di 1 è detta essere primitiva se non è anche
una radice m-esima di 1 per qualche divisore positivo m 6= n di n. Dimostrare
che
a) w è una radice primitiva n-esima di 1 se e solo se w = ξnk dove k è un
intero tale che MCD(k, n) = 1.
b) w è una radice primitiva n-esima di 1 se e solo se ogni radice n-esima u di
1 si scrive nella forma u = wh per qualche intero h.
Esercizio. Dato un numero complesso non nullo z = a + ib = ρ(cos θ + i sen θ)
dimostrare che, posto w = ρ1/n (cos(θ/n) + i sen(θ/n)), i numeri complessi
w, wξn , wξn2 , . . . , wξnn−1 sono tutte e sole le radici n-esime di z.
Esercizio. Siano Un = ξn0 , ξn , ξn2 , . . . , ξnn−1 e S un sottoinsieme di C \ {0}
con n elementi, tale che comunque siano scelti z, w ∈ S si ha che il prodotto zw
appartiene anch’esso a S. Dimostrare che S = Un .
Esempio (radici quinte dell’unità). Supponiamo che ε 6= 1 sia una radice quinta
di 1. Essa soddisfa l’equazione 0 = ε5 − 1 = (ε − 1)(1 + ε + ε2 + ε3 + ε4 ). Dal
45
momento che ε 6= 1 se ne deduce che
1 + ε + ε2 + ε3 + ε4 = 0.
Notiamo che ε4 · ε = 1 pertanto ε4 = ε−1 = ε̄/|ε|2 = ε̄. Analogamente si ha che
ε3 = (ε2 )−1 = (ε−1 )2 = ε̄2 . Posto γ = ε + ε4 si ha che γ = ε + ε̄ = 2 Re(ε) e che
γ 2 = ε2 + ε8 + 2 = ε2 + ε3 + 2. Ne deduciamo che
γ 2 + γ − 1 = (ε2 + ε3 + 2) + (ε + ε4 ) − 1 = 1 + ε + ε2 + ε3 + ε4 = 0
e che pertanto γ è radice dell’equazione di secondo grado
x2 + x − 1 = 0
Possiamo allora calcolare
√
−1 ± 5
γ=
2
2π
Nell’ipotesi che sia ε = ξ5 = cos 5 + i sen
√
quindi γ = 5−1
2 . Se ne ricava che
2π
5
, allora γ = 2 Re(ε) > 0 e
√
5−1
,
4
s
s
√
√
s
2π
2π
6
−
2
5
1
5+ 5
2
sen
= 1 − cos
= 1−
=
.
5
5
16
2
2
cos
2π
5
= γ/2 =
Esercizio. Con riferimento all’esempio precedente mostrare che che se ε = ξ5
7
allora −ε = ξ10
è una radice primitiva decima di 1. Determinare inoltre il più
piccolo intero positivo k tale che ξ10 = (−ε)k .
46