Esercitazione n° 2 FISICA
SPERIMENTALE I
(C.L. Ing. Edi.)
(Prof. Gabriele Fava)A.A. 2010/2011
Cinematica
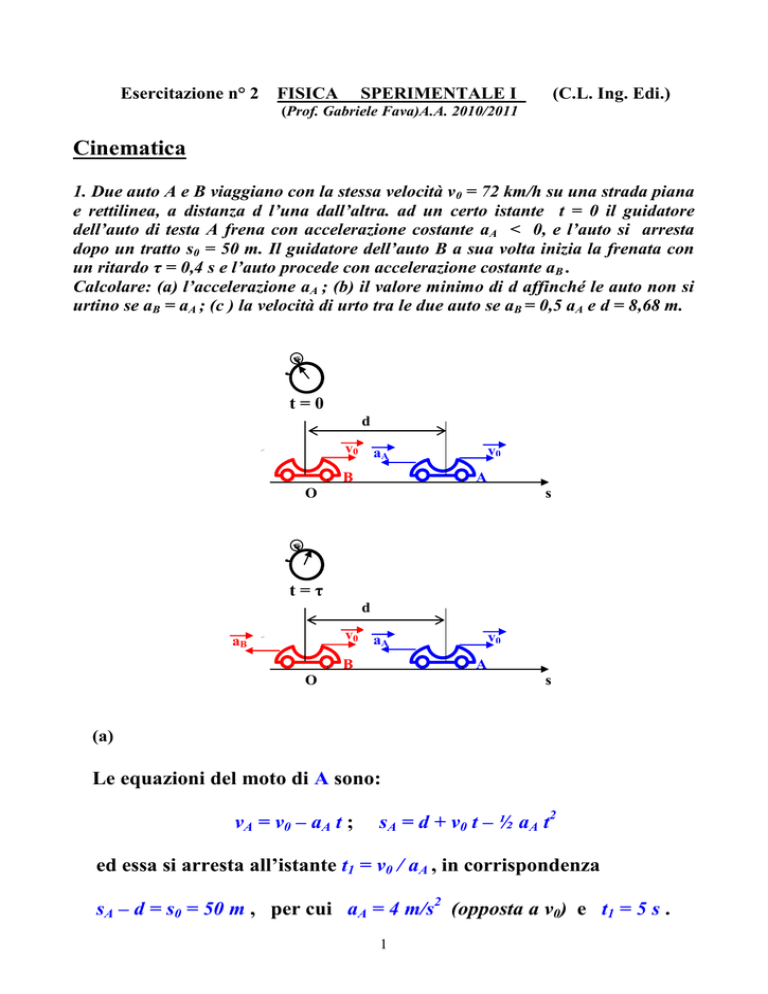
1. Due auto A e B viaggiano con la stessa velocità v0 = 72 km/h su una strada piana
e rettilinea, a distanza d l’una dall’altra. ad un certo istante t = 0 il guidatore
dell’auto di testa A frena con accelerazione costante aA < 0, e l’auto si arresta
dopo un tratto s0 = 50 m. Il guidatore dell’auto B a sua volta inizia la frenata con
un ritardo τ = 0,4 s e l’auto procede con accelerazione costante aB .
Calcolare: (a) l’accelerazione aA ; (b) il valore minimo di d affinché le auto non si
urtino se aB = aA ; (c ) la velocità di urto tra le due auto se aB = 0,5 aA e d = 8,68 m.
t=0
d
v0 aA
a’
B
v0
A
O
s
t=τ
d
v0 aA
a’
B
aB
O
v0
A
s
(a)
Le equazioni del moto di A sono:
vA = v0 – aA t ;
sA = d + v0 t – ½ aA t2
ed essa si arresta all’istante t1 = v0 / aA , in corrispondenza
sA – d = s0 = 50 m , per cui aA = 4 m/s2 (opposta a v0) e t1 = 5 s .
1
(b)
Il moto di B per t ≤ τ è dato da vB = v0 ; sB = v0 t ,
mentre per il tempo t ≥ τ le equazioni diventano
vB = v0 – aB (t – τ) ; sB = v0 t – ½ aB (t – τ)2 .
Dato che aA = aB, affinché non avvenga l’urto occorre che B giunga
con velocità minore di v0 nel punto in cui A ha iniziato a rallentare,
cioè d deve essere maggiore dello spazio che B percorre
nell’intervallo di tempo che va da t = 0 a t = τ.
La condizione perciò è d > v0 τ = 8 m.
(c)
In questo caso risultano aB = 2 m/s2 e d = 8,68 m .
La condizione di urto si traduce nell’equazione sA (t2) = sB (t2) ,
essendo t2 l’istante dell’urto stesso, cioè:
d + v0 t2 – ½ aA t22 = v0 t2 – ½ aB (t2 – τ)2 da cui t2 = 2,6 s .
Al tempo t2 : vA = v0 – aA t2 = 9,6 m/s ; vB = v0 – aB (t2 – τ) = 15,6 m/s
(d)
La velocità relativa al momento dell’urto vale vr = vB – vA = 6 m/s .
2
2. Un sasso viene lanciato da terra con una velocità v0 = 20 m/s.
(a) Calcolare per quali valori dell’angolo di lancio il sasso passa per il punto
R di coordinate xR = 30 m, yR = 7 m.
(b) Determinare le componenti tangenziale e radiale della accelerazione nel
generico punto P(x,y) della traiettoria.
y
g
vo
O
voy
α
vox
x
(a)
x = v0x t
v0x = v0 cosα
y = v0y t – ½ gt2
v0y = v0 senα
Le equazioni del moto sono
Ricavando t dalla prima equazione e sostituendo nella seconda si
ottiene l’equazione cartesiana della traiettoria:
g
y x tg 2
x 2 che risulta essere una parabola con asse
2
2v0 cos
verticale e concavità rivolta verso il basso.
1
1 tg 2 , sostituendo nell’equazione della
2
cos
traiettoria e imponendo il passaggio per il punto R, si ottiene:
Ricordando che
yR xR tg
g
2
1 tg 2 xR e con i valori dati
2
2v0
11 tg2 α – 30 tgα + 18 = 0
tgα = 1,84
tgα = 0,89
α = 61,5°
α = 41,7°
3
(b)
In generale
dv v 2
a n
dt
r
dv
at è l’accelerazione
dove
dt
v2
an è l’accelerazione normale (centripeta) .
tangenziale e
r
Nel nostro caso vx = v0x = v0 cosα ; vy = v0y – gt = v0 senα – gt , per cui
v v x2 v y2 v02 2v0 sen gt g 2t 2
dv
at
Dunque
dt
v0 g sen g 2 t
v02 2v0 gt sen g 2 t 2
Per trovare l’accelerazione normale occorre ricordare che, data la
curva di equazione y = f(x), per il raggio di curvatura vale la
relazione:
d2y
dx 2
1
3
r
2
2
dy
1
dx
Nel nostro caso si ottiene
gv0 cos
1
r v02 2 gt v0 sen g 2t 2 v02 2 gtv0 sen g 2t 2
per cui
gv0 cos
v2
an
.
r
v02 2 gt v0 sen g 2t 2
4
3. Un corpo si muove con velocità costante in modulo lungo una traiettoria
parabolica di equazione y = b x2 con b costante positiva. Determinare le
componenti della velocità e dell’accelerazione in funzione di x, calcolando in
particolare l’accelerazione del corpo in x = 0. Determinare inoltre l’espressione del
raggio di curvatura.
v
α
Con riferimento alla figura, si ha:
v tg
v
v y v sen
v x v cos
;
1 tg 2
1 tg 2
dy
2bx arctg 2bx , cosicché il valore di α varia da
e dato che tg
dx
punto a punto. Le componenti della velocità diventano:
vx x
v
1 4b 2 x 2
; v y x
2bvx
1 4b 2 x 2
Da queste espressioni si ricavano le componenti della accelerazione:
dvx dvx dx dvx
4b 2 v 2 x
a x x
vx
dt
dx dt
dx
1 4b 2 x 2
dv y dx dv y
2bv 2
a y x
vx
dt
dx dt
dx
1 4b 2 x 2
dv y
2
2
Nell’origine x = y = 0 ; vx = v ; vy = 0 ; ax = 0 ; ay = 2bv2, dal che si vede che
l’accelerazione è puramente centripeta. Si osservi che ciò non è caratteristico
della sola origine, ma è vero ovunque, essendo il moto uniforme.
Il modulo della accelerazione è ax
1 4b x
r x
2
cui
2b
2
3
a a
2
x
2
y
2bv 2
1 4b x
2
2
3
2
v2
an , da
r
2
, raggio di curvatura; in particolare r (0) = 1 / 2b.
5
4. Una sferetta viene lanciata dalla origine
degli assi nello stesso istante in cui
un’altra sferetta viene lasciata cadere
dal punto di coordinate ( x0 , y0 ).
(a) Dimostrare che, se la prima sferetta
viene lanciata verso il punto di partenza
della seconda, le due si incontrano con
qualunque valore della velocità di lancio
della prima.
(b) Determinare le coordinate ( xi , yi ) del punto di incontro in funzione
della velocità di lancio.
(a)
le equazioni relative al moto delle due sferette sono:
Pallina lanciata
x1 = v0x t = v0 cosα ∙ t ; y1 = voy t – ½ g t2 = v0 senα ∙ t – ½ g t2
Pallina lasciata cadere
x2 = x0 ; y2 = y0 – ½ g t2
y0
tg
Inoltre si ha
x0
La condizione per l’incontro è data da: x1 = x2 ; y1 = y2 per lo stesso
valore di t, cioè
v0 cosα ∙ t = x0
v0 senα ∙ t – ½ g t2 = y0 – ½ g t2
v0 sen t y 0
da cui si ricava v cos t x tg e, quindi, l’incontro nelle
0
0
condizioni date avviene sempre.
x0
y0
(b) Le coordinate del punto di incontro al tempo ti v cos v sen
0
0
sono: xi = x0 ;
gx02
yi y 0 2
2v0 cos 2
.
6
5. Un’asta AC di lunghezza d si può muovere con
gli estremi vincolati a scorrere lungo gli assi
x e y rispettivamente.
Se il punto A si muove con velocità costante vA ,
calcolare:
(a) la velocità e l’accelerazione del punto C;
(b) il moto del punto B posto a metà dell’asta.
d
2
2
2
2 2
La posizione del punto C è data da xC = 0 ; yC d x A d v At ,
dyC
v A2 t
x Av A
vC
dt
d 2 v A2 t 2
d 2 x A2
quindi
dvC
v A2 d 2
aC
dt
d 2 v A2 t 2
3
2
d
v A2 d 2
2
x A2
3
2
Il punto B ha coordinate xB = xA / 2 , yB = yC / 2
xB2 + yB2 = d2 / 4, e
quindi B si muove su una circonferenza di centro O (0,0) e raggio d / 2.
percorsa in verso orario. Calcoliamo ora velocità e accelerazione di B.
v Bx
dx B 1 dx A v A
dyB 1 dyC vC
v
By
dt
2 dt
2
dt
2 dt
2 ;
aBx
dv
dvBx 1 dv A
1 dvC aC
0 ; aBy By
dt
2 dt
2
dt
2 dt
x
d
cos x B A
2
2
y
d
sen yB C ,
2
2
d
d
vA
sen
derivando la (A) si ottiene (C)
e sostituendo in
2
dt
2
d
d
d v A
sen
y
B
essa la (B) si ha
da cui
2
dt
dt
2
d
v
v
vA
A A
velocità angolare non costante,
2
2 2
dt
2 yB
yC
d vA t
E poiché (A)
e
quindi moto vario.
7
(B)
6. Una pallina, lanciata con velocità v0
dall’estremo A di una guida circolare liscia
di raggio R, la abbandona all’altro estremo C.
Dati R = 10 cm e v0 = 5 m/s, calcolare:
a) la velocità della pallina nel punto C;
b) il punto G dell’asse x in cui essa cade.
vCx = v0 cos 60°
g
vCy = v0 sen 60°
(a)
ZH = h = R cos 60° = R / 2 ; vC2 = v02 + 2gh = v02 + gR
vC = 5,1 m/s
(b)
x = xC + vCx t (I)
con xC = R sen 60°
Oltre il punto C
y = yC + vCy t – ½ gt2 (II) con yC = R cos 60°
Nel punto G di caduta yG = 0 per cui la (II) diventa:
0 = yC + vCy tv – ½ gtv2
dove tv è il tempo di volo > 0.
Si ricava tv = 1,5 s e in corrispondenza a questo tempo dalla (I) segue
xG = xC + vCx tV = 3,88 m .
8
7. Dalla quota h0 = 5 m si lancia orizzontalmente una pallina di gomma con
velocità v0 = 10 m/s.
(a) Calcolare la gittata s1 , la velocità di arrivo a terra e l’angolo α che questa
forma col terreno all’istante dell’urto.
(b) Sapendo che nell’urto le due componenti della velocità diminuiscono del 20% ,
calcolare l’altezza massima raggiunta dopo il primo rimbalzo e la distanza s 2 da O
del successivo punto di arrivo della pallina a terra.
g
x = v0 t
Le equazioni del moto sono
y = h0 – ½ gt2
Ricavando t dalla prima equazione e sostituendo nella seconda si
ottiene l’equazione cartesiana della traiettoria:
g
y h0 2 x 2 che risulta essere una parabola con asse verticale,
2v0
vertice sull’asse y e concavità rivolta verso il basso.
(a)
Quando la pallina tocca terra y = 0, per cui la gittata si ottiene
2h
g 2
s
v
10 m .
0
h
s
1
0
0
1
2
dall’equazione
g
2v0
9
Le componenti della velocità in tale istante sono:
vx v0 10 m / s ; v y 2 gh 10 m / s , per cui
vx
tg
vy
3
1
vx
4
vy
(b)
Nell’urto le componenti della velocità diventano
vy*
v *x 8 m / s
v*y 8 m / s
vx*
2h
1 s il tempo di volo della pallina, successivamente
g
Essendo t v
all’urto si ha:
x = s1 + vx* (t – tv) ; y = vy* (t – tv) – ½ g (t – tv)2
vx = vx* ; vy = vy* - g (t – tv)
In corrispondenza alla quota massima la componente vy = 0 e ciò si
verifica nell’istante t = tv + vy* / g , in corrispondenza le coordinate
della pallina sono:
2
v *x v *y
v*x
x1 s1
16,4 m
y1
hMAX 3,2 m
2g
g
Infine s2 = s1 + 2 (x1 – s1) = 22,8 m .
10
8. Si consideri un triangolo equilatero ABC di lato l = 10 m. All’istante t = 0 due
punti materiali partono contemporaneamente dal vertice A, P1 lungo il lato AB
con accelerazione a1 = 2 m/s2, P2 lungo AC con a2 = 1,5 m/s2.
Dopo un tempo τ un terzo punto P3 inizia a muoversi sul lato BC, di moto
armonico con centro in H, pulsazione ω, ampiezza s0 = ½ l.
Si determini il valore che debbono assumere τ ed ω affinché il terzo punto tocchi
successivamente gli altri due al passaggio di essi rispettivamente per i punti B e C.
Equazioni orarie:
P1
s 1 = ½ a 1 t2
tempo per giungere in B
t1
2l
a1
P2
s 2 = ½ a 2 t2
tempo per giungere in C
t2
2l
a2
P3
s3 = s0 sen ω (t – τ) prendendo positivo il verso da H a B.
Perché si abbiano le coincidenze richieste dal problema dovrà essere:
s0 sen ω (t1 – τ) = s0 (contatto con P1)
s0 sen ω (t2 – τ) = − s0 (contatto con P2)
Dividendo membro a membro si ottiene:
11
ω (t1 – τ) = π/2 + 2n1π (I)
ω (t2 – τ) = 3/2 π + 2n2π (II)
t 2 3 4n 2
t1 1 4n1
da cui
t1 3 4n2 t 2 1 4n1
(III).
2 4 n2 n1
Dato che dalla (I) si
ottiene 2
2n1
t1
sostituendo in essa la (III) si ha:
1 2 n2 n1
.
t 2 t1
Dovendo essere ω > 0 ed essendo t2 > t1 dato che a2 < a1 dovrà risultare
n2 – n1 = numero intero ≥ 0.
Si avranno allora ∞2 soluzioni
n1 = 0, 1, 2, 3, …….
;
n2 = n1, n1 +1, n1 +2, n1 +3,…..
Nel caso particolare in cui n2 – n1 = 0, cioè n2 = n1 risulta:
t 2 t1
T = 2 (t2 – t1)
1
3t1 t 2
2
P3 toccherà P1 e P2 nel corso di una semioscillazione.
12
9. Un corpo puntiforme C si muove con velocità costante v lungo un’asta rigida
AB che, a sua volta, ruota sul piano della figura con velocità angolare costante
ω attorno al suo estremo A.
Se all’istante t = 0 il punto C si trova in A, determinare le componenti dei suoi
vettori posizione, velocità e accelerazione rispetto al sistema Oxy fisso, con
origine in A e asse delle x coincidente con la direzione dell’asta al tempo t = 0.
y
B
r
θ=ωt
O≡A
r ≡
rx = v t cos ωt
x
v ≡
ry = v t sen ωt
a ≡
vx = v cos ωt – v ω t sen ωt
vy = v sen ωt + v ω t cos ωt
ax = - 2 v ω sen ωt – v ω2 t cos ωt
ay = 2 v ω cos ωt - v ω2 t sen ωt
13