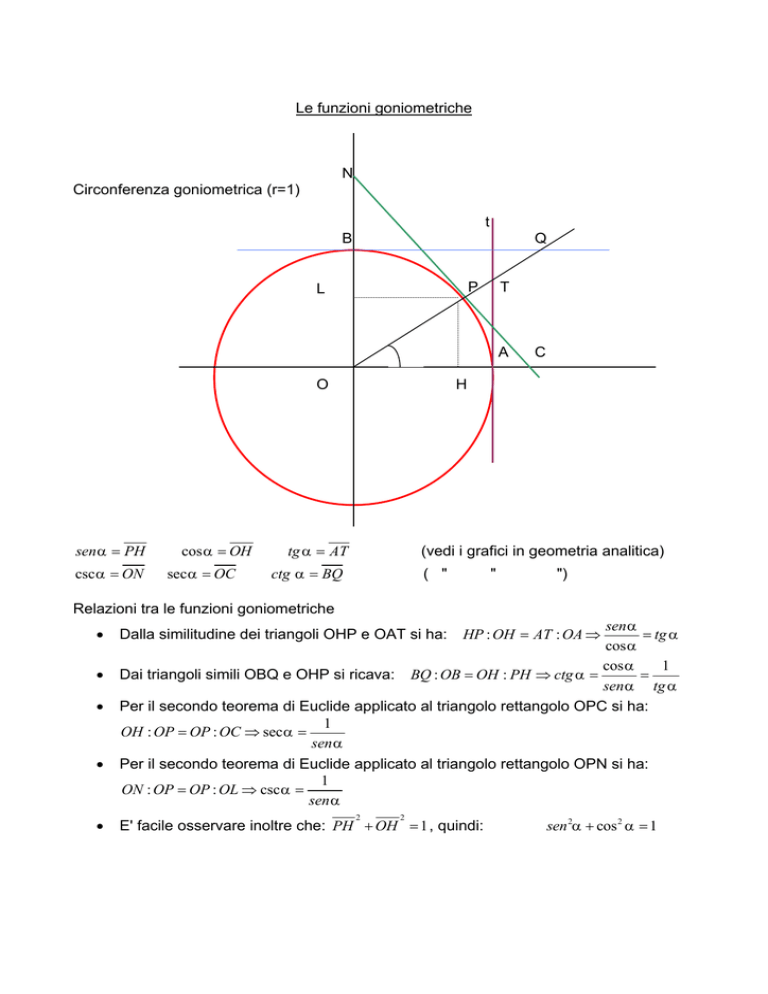
Le funzioni goniometriche
N
Circonferenza goniometrica (r=1)
t
B
Q
P
L
T
A
α
O
sen α = PH
csc α = ON
cos α = OH
sec α = OC
C
H
tg α = AT
(vedi i grafici in geometria analitica)
ctg α = BQ
( "
"
")
Relazioni tra le funzioni goniometriche
•
•
•
•
•
sen α
= tg α
cos α
cos α
1
Dai triangoli simili OBQ e OHP si ricava: BQ : OB = OH : PH ⇒ ctg α =
=
sen α tg α
Per il secondo teorema di Euclide applicato al triangolo rettangolo OPC si ha:
1
OH : OP = OP : OC ⇒ sec α =
sen α
Per il secondo teorema di Euclide applicato al triangolo rettangolo OPN si ha:
1
ON : OP = OP : OL ⇒ csc α =
sen α
Dalla similitudine dei triangoli OHP e OAT si ha:
2
2
HP : OH = AT : OA ⇒
E' facile osservare inoltre che: PH + OH = 1 , quindi:
sen 2α + cos 2 α = 1
Angoli particolari (*)
1. α =
π
6
senα =
2. α =
π
3
senα =
3
2
cos α =
1
2
3. α =
π
4
senα =
2
2
cos α =
2
2
4. α =
π
10
senα =
1
2
cos α =
5 −1
4
(*)visita la pagina geometria piana
cos α =
3
2
tg α =
10 + 2 5
4
3
3
tg α = 3
tg α = 1
tg α =
5−2 5
5












