MATEMATICA
PROGRAMMA 4I
2015-2016
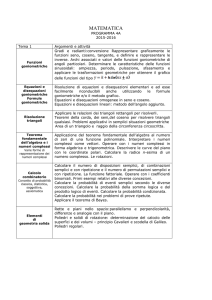
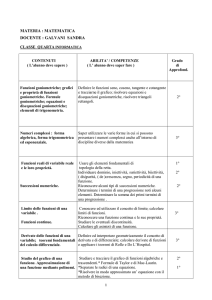
Tema 1
Funzioni
goniometriche
Argomenti e attività
Gradi e radianti:conversione Rappresentare graficamente le
funzioni seno, coseno, tangente, e definire e rappresentare le
inverse. Archi associati e valori delle funzioni goniometriche di
angoli particolari. Determinare le caratteristiche delle funzioni
sinusoidali: ampiezza, periodo, pulsazione, sfasamento e
applicare le trasformazioni geometriche per ottenere il grafico
delle funzioni del tipo
Equazioni e
disequazioni
goniometriche
Formule
goniometriche
Risoluzione di equazioni e disequazioni elementari e ad esse
facilmente
riconducibili
anche
utilizzando
le
formule
goniometriche e/o il metodo grafico.
Equazioni e disequazioni omogenee in seno e coseno.
Equazioni e disequazioni lineari: metodo dell’angolo aggiunto.
Risoluzione
triangoli
Applicare le relazioni dei triangoli rettangoli per risolverli.
Teoremi della corda, dei seni,del coseno per risolvere triangoli
qualsiasi. Problemi applicativi in semplici situazioni geometriche
Area di un triangolo e raggio della circonferenza circoscritta.
Teorema
fondamentale
dell’algebra e i
numeri complessi
Varie forme di
rappresentazione dei
numeri complessi
Calcolo
combinatorio
Concetto di probabilità
classica, statistica,
soggettiva,
assiomatica
Elementi
di
geometria solida
Applicazione del teorema fondamentale dell’algebra al numero
di zeri di una funzione polinomiale. Interpretare i numeri
complessi come vettori. Operare con i numeri complessi in
forma algebrica e trigonometrica. Descrivere le curve del piano
con le coordinate polari. Calcolare la radice n-esima di un
numero complesso. Le rotazioni.
Calcolare il numero di disposizioni semplici, di combinazioni
semplici e con ripetizione e il numero di permutazioni semplici e
con ripetizione. La funzione fattoriale. Operare con i coefficienti
binomiali. Primi esempi relativi alle diverse concezioni.
Calcolare la probabilità di eventi semplici secondo le diverse
concezioni. Calcolare la probabilità della somma logica e del
prodotto logico di eventi. Calcolare la probabilità condizionata.
Calcolare la probabilità nei problemi di prove ripetute.
Applicare il teorema di Bayes.
Rette e piani nello spazio:parallelismo e perpendicolarità,
differenze e analogie con il piano.
Poliedri e solidi di rotazione: determinazione del calcolo delle
superfici e dei volumi – principio Cavalieri e scodella di Galileo.
Poliedri regolari.