MATERIA : MATEMATICA
DOCENTE : GALVANI SANDRA
CLASSE QUARTA INFORMATICA
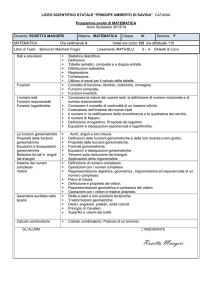
CONTENUTI
( L’alunno deve sapere )
ABILITA’ / COMPETENZE
( L’ alunno deve saper fare )
Funzioni goniometriche; grafici
e proprietà di funzioni
goniometriche. Formule
goniometriche; equazioni e
disequazioni goniometriche;
elementi di trigonometria.
Definire le funzioni seno, coseno, tangente e cotangente
e tracciarne il grafico; risolvere equazioni e
disequazioni goniometriche, risolvere triangoli
rettangoli.
Numeri complessi : forma
algebrica, forma trigonometrica
ed esponenziale.
Saper utilizzare le varie forme in cui si possono
presentare i numeri complessi anche all’interno di
discipline diverse dalla matematica
Funzioni reali di variabile reale
e le loro proprietà.
Usare gli elementi fondamentali di
topologia della retta.
Individuare dominio, iniettività, suriettività, biiettività,
( dis)parità, ( de )crescenza, segno, periodicità di una
funzione.
Riconoscere alcuni tipi di successioni numeriche.
Determinare i termini di una progressione noti alcuni
elementi. Determinare la somma dei primi termini di
una progressione .
Successioni numeriche.
Limite delle funzioni di una
variabile .
Funzioni continue.
Conoscere ed utilizzare il concetto di limite; calcolare
limiti di funzioni.
Riconoscere una funzione continua e le sue proprietà.
Studiare le eventuali discontinuità.
Calcolare gli asintoti di una funzione.
Definire ed interpretare geometricamente il concetto di
Derivate delle funzioni di una
variabile; teoremi fondamentali derivata e di differenziale; calcolare derivate di funzioni
e applicare i teoremi di Rolle e De L’Hospital.
del calcolo differenziale.
Studiare e tracciare il grafico di funzioni algebriche e
Studio del grafico di una
trascendenti.* Formule di Taylor e di Mac-Laurin.
funzione. Approssimazione di
una funzione mediante polinomi. *Separare le radici di una equazione.
*Risolvere in modo approssimato un’ equazione con il
metodo di bisezione.
1
Grado
di
Approfond.
2°
3°
1°
2°
2°
3°
3°
2°
1°
La statistica e le basi
dell’inferenza.
Studiare le distribuzioni di dati, classificarli e
rappresentarli graficamente; riconoscere le diverse
componenti delle distribuzioni.
Calcolare gli indici di variabilità e di posizione centrale.
2°
Calcolo combinatorio.
Calcolare il numero di permutazioni, distribuzioni e
combinazioni di un insieme. Applicare le proprietà del
coefficiente binomiale, sviluppare la potenza di un
binomio.
2°
Probabilità
Studiare gli eventi nella concezione classica e nella
concezione statistica della probabilità.
2°
*Argomenti riguardanti COMPLEMENTI DI MATEMATICA
LIVELLI DI APPROFONDIMENTO
1°- Conoscenze fondamentali, esercizi semplici ( obiettivi minimi ).
2°- Conoscenze complete, esercizi strutturati.
3°- Conoscenze ampie e dettagliate, esercizi di applicazione e di rielaborazione
2
3