Misure delle mediane e delle bisettrici di un triangolo ( )

Misure delle mediane e delle bisettrici di un triangolo
Mediane
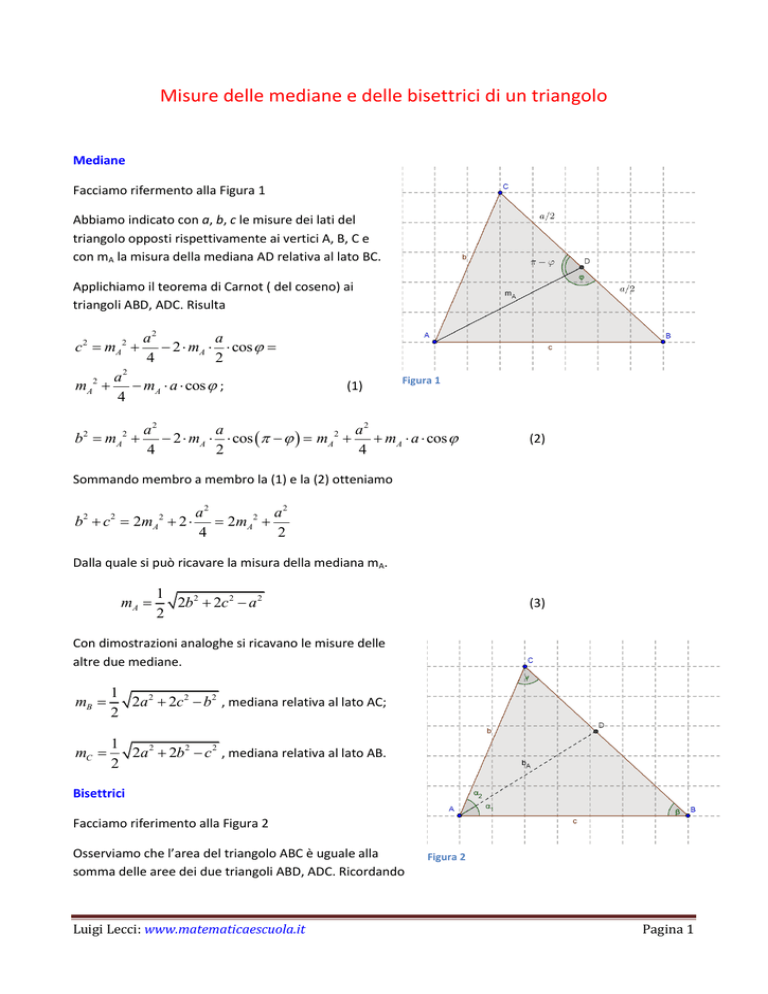
Facciamo rifermento alla Figura 1
Abbiamo indicato con a, b, c le misure dei lati del
triangolo opposti rispettivamente ai vertici A, B, C e
con mA la misura della mediana AD relativa al lato BC.
Applichiamo il teorema di Carnot ( del coseno) ai
triangoli ABD, ADC. Risulta
c 2  mA 2 
mA 2 
a2
a
 2  mA   cos  
4
2
a2
 mA  a  cos  ;
4
b 2  mA 2 
(1)
Figura 1
a2
a
a2
 2  mA   cos      mA2   mA  a  cos 
4
2
4
(2)
Sommando membro a membro la (1) e la (2) otteniamo
b 2  c 2  2mA 2  2 
a2
a2
 2mA 2 
4
2
Dalla quale si può ricavare la misura della mediana mA.
mA 
1
2b2  2c 2  a 2
2
(3)
Con dimostrazioni analoghe si ricavano le misure delle
altre due mediane.
mB 
1
2a 2  2c 2  b 2 , mediana relativa al lato AC;
2
mC 
1
2a 2  2b 2  c 2 , mediana relativa al lato AB.
2
Bisettrici
Facciamo riferimento alla Figura 2
Osserviamo che l’area del triangolo ABC è uguale alla
somma delle aree dei due triangoli ABD, ADC. Ricordando
Luigi Lecci: www.matematicaescuola.it
Figura 2
Pagina 1
che l’area di un triangolo si può trovare come il semiprodotto delle misure di due lati per il seno dell’angolo
compreso tra i due si ha:
S ABC  S ABD  S ADC
1
1
1
bc  sen  bA  c  sen1  bA  b  sen 2
2
2
2
Nella (3) risulta 1   2 

2
(3)
.
Applichiamo ora la formula di duplicazione per sen(), considerando   2 

2
.
1
 
  1
  1
 
bc  2sen   cos    bA  c  sen    bA  b  sen  
2
2
2 2
2 2
2
 
 si ottiene
2
Semplificando sen 
1
  1
bc  cos    bA  c  bA  b ,
2
2 2
da cui si ricava la misura della bisettrice relativa all’angolo del vertice A.
bA 
2bc
 
 cos  
bc
2
(4)
Con analoghi procedimenti si trovano le misure delle bisettrici del triangolo relative agli altri due angoli.
bB 
2ac
 
 cos   , per la bisettrice dell’angolo nel vertice B;
ac
2
bC 
2ab
 
 cos   , per la bisettrice dell’angolo nel vertice C.
ab
2
Luigi Lecci: www.matematicaescuola.it
Pagina 2