3 Geometria delle masse e momento di 2° ordine
3.2 Momento d’inerzia di superfici piane e modulo di resistenza
1
3.2.1 Momenti di inerzia assiali di superfici piane regolari
Momento d’inerzia rispetto all’asse y0 coincidente con una mediana
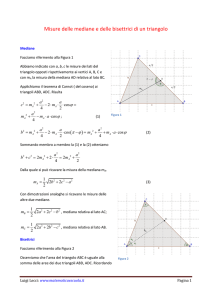
La mediana divide il triangolo dato in due triangoli aventi in
comune la base BE = h⬘ e la medesima altezza (AA⬘ = CC⬘ = b⬘);
il momento d’inerzia del triangolo dato rispetto all’asse y0 è
quindi fornito dalla somma dei momenti d’inerzia dei due triangoli rispetto alla base BE:
1
Iy0 = 2 ⫻
⋅ h⬘⋅ b⬘3
12
quindi:
0
Iy =
0
1
b3
⋅ h ′ ⋅ ⋅sen 3 α
6
8
ossia:
0
Iy =
0
1
⋅ h ′ ⋅ b3 ⋅sen 3 α
48
0
ma:
b′ =
b
⋅sen α
2
© SEI - 2012