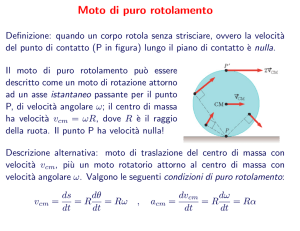
Il moto di puro rotolamento
Ilmotodipurorotolamentoèunmotoincuiilpuntodiconta<otra
lasuperficieedilcorpocherotola(asezionecircolare)èfermoistante
peristante:vP=0.Ricordiamoche,grazieaiteoremidiKönig,
possiamoseparareilmotorototraslatorioinrotazionedelcorpo
rispe<oalsuoCM,etraslazionedelCMrispe<oallaboratorio.
v = ωR
v = ωR + vCM
v = ωR
vP = -ωR
vO = 0
vT = ωR
FisicaGeneraleI
v = ωR - vCM = 0
vP = vCM
vO = vCM
vT = vCM
vP = vCM – ωR
vO = vCM
vT = vCM + ωR
A.A.2016/17
vP = 0 ⇒
}⇒ v
CM
= ωR
2
Sia µs il coefficiente di attrito statico
tra il piano e il corpo rigido e
R M
supponiamo che il corpo sia fermo
quando inizia il moto e si trovi ad
h
un’altezza h dal suolo. Sia inoltre I’
il momento d’inerzia del corpo
θ
rispetto ad un asse passante per il
CM e ⊥ al foglio.
NB l’attrito statico non e’ l’attrito statico massimo in generale.
All’istante t = 0 s il corpo viene lasciato libero di muoversi e scende
lungo il piano inclinato con velocità angolare ω; il moto è fin dall’inizio
di puro rotolamento.
Emi = Em f
FisicaGeneraleI
Mgh =
1
1
2
MvCM
+ I 'ω 2
2A.A.2016/17
2
3
Ricordando la condizione di puro rotolamento, vCM = ωR, si ha
2
1 2
1 ' vCM
mgh = mvCM + I 2
2
2 R
!
$
# 1 &
2
&
vCM
= 2gh #
'
## 1+ I &&
" mR 2 %
I ' = mR 2
1
I ' = mR 2
2
2
I ' = mR 2
3
FisicaGeneraleI
Ricordiamo ora che il rapporto tra
I’ ed R è proporzionale ad m, il
coefficiente di proporzionalità
dipendendo dalla geometria del corpo
anello
vCM = gh
cilindro
vCM =
sfera cava
vCM
A.A.2016/17
4
gh
3
6
=
gh
5
4
IrisultaRcosìo<enuRvannoconfrontaRconquelliricavaRnelcasoin
cuiilcorporigidochescendesenzarotolaredallastessaaltezzalungoun
pianoliscioconlostessoangolodiinclinazione
θ, sappiamogiàche
o<eniamoperognicorpolostessorisultato, vCM = √2gh.
Ladifferenzatralevelocitào<enuteneiduecasi(entrambiconservaRvi
dalpuntodivistaenergeRcoeconlamedesimaEminiziale)èdovuta
alfa<oche,nelcasodelpurorotolamento,ilcorpodeveimpiegare
partedellasuaenergiapotenzialegravitazionaleperentrarein
rotazione,ciòadiscapitodellatraslazione.Comeconseguenza,nelcaso
delpurorotolamento,abbiamovelocitàfinalidelCMpiùpiccole.
Esaminiamoorailproblemadalpuntodivistadinamico.Scriviamole
dueequazionicardinalidelladinamicaperilcorporigido(rotazione
a<ornoadunasseprincipaled’inerziasenzapuntofissoinun
sistemainerziale)
!'
!
⎧ M ext = I 'α
⎨ !
!
⎩∑ Fext = MaCM
FisicaGeneraleI
A.A.2016/17
5
Prendiamo come polo il CM; la forza peso , essendo applicata nel CM
non produce momento. Solo la forza di attrito fs produce momento.
NB: Momento d'inerzia rispetto CM = I '
⎧⎪ Rfs = I 'α
⎨ ! ! !
!
⎪⎩ mg + fs + N = maCM
aCM = α R
⎧
I ' aCM
f
=
⎪ s
R2
⎪⎪
⎨ mgsin ϑ − fs = maCM
⎪
⎪ N − mgcosϑ = 0
⎪⎩
FisicaGeneraleI
A.A.2016/17
6
IN ALTERNATIVA SPESSO PIU” CONVENIENTE prendiamo come
polo il punto di contatto P del disegno; la forza di attrito fs, essendo
applicata al punto P non produce momento. Solo il peso produce
momento rispetto il polo P (la componente normale al braccio r e’
mgsin(θ) )
NB: Momento d'inerzia rispetto P
I P = I ' + mR 2
⎧⎪ Rmgsin ϑ = I P' α
⎨ ! ! !
!
⎪⎩ mg + fs + N = maCM
R2
mgsin ϑ '
= α R = aCM
I + mR 2
mgsin ϑ − fs = maCM
I ' aCM
fs = 2
R
FisicaGeneraleI
A.A.2016/17
7