Amplificatore differenziale
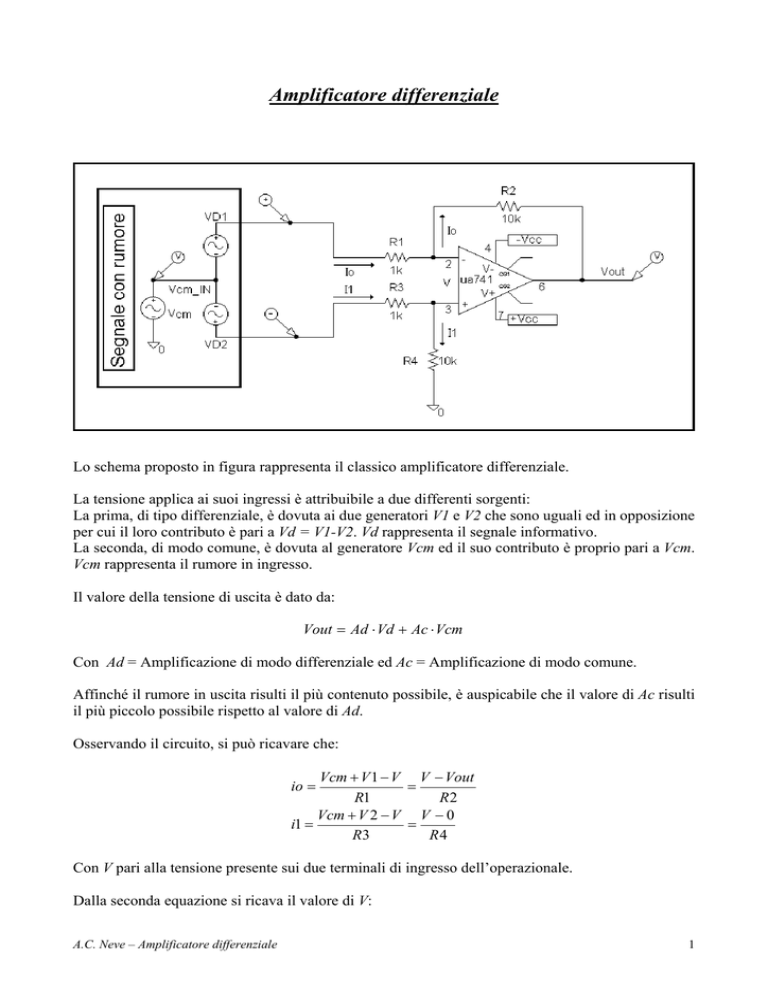
Lo schema proposto in figura rappresenta il classico amplificatore differenziale.
La tensione applica ai suoi ingressi è attribuibile a due differenti sorgenti:
La prima, di tipo differenziale, è dovuta ai due generatori V1 e V2 che sono uguali ed in opposizione
per cui il loro contributo è pari a Vd = V1-V2. Vd rappresenta il segnale informativo.
La seconda, di modo comune, è dovuta al generatore Vcm ed il suo contributo è proprio pari a Vcm.
Vcm rappresenta il rumore in ingresso.
Il valore della tensione di uscita è dato da:
Vout = Ad ⋅ Vd + Ac ⋅ Vcm
Con Ad = Amplificazione di modo differenziale ed Ac = Amplificazione di modo comune.
Affinché il rumore in uscita risulti il più contenuto possibile, è auspicabile che il valore di Ac risulti
il più piccolo possibile rispetto al valore di Ad.
Osservando il circuito, si può ricavare che:
Vcm + V 1 − V V − Vout
=
R1
R2
Vcm + V 2 − V V − 0
i1 =
=
R3
R4
io =
Con V pari alla tensione presente sui due terminali di ingresso dell’operazionale.
Dalla seconda equazione si ricava il valore di V:
A.C. Neve – Amplificatore differenziale
1
Vcm + V 2
1
1
= V ⋅
+
R3
R3 R 4
⇒
V =
Vcm + V 2
Vcm + V 2
=
R3
1
1
1+
R3 ⋅
+
R4
R3 R 4
Dalla prima equazione si ha invece che:
Vcm + V 1
1 Vout
1
= V ⋅ +
−
R1
R1 R 2 R 2
⇒
R1 R1
Vcm + V 1 = V ⋅ 1 +
⋅ Vout
−
R2 R2
Sostituendo in quest’ultima l’espressione trovata in precedenza per V, si ha che:
1+
Vcm ⋅ 1 −
1+
R1
1+
R2 + V 1 − V 2 ⋅
R3
1 +
R 4
R1
R 2 = − R1 ⋅ Vout
R3
R2
R4
Il termine che moltiplica Vcm rappresenta l’amplificazione di modo comune e può essere reso nullo
imponendo l’uguaglianza:
R1 R3
=
R2 R4
Si ha quindi che:
Vout = −
R2
⋅ (V 1 − V 2 )
R1
con
R2
= Ad
R1
In queste condizioni l’uscita dipende soltanto dalla tensione di ingresso differenziale e non risente
di eventuali segnali di rumore presenti sull’ingresso.
Assegnando al circuito proposto i seguenti valori si ha che:
V1 = 0.5 volt 40 Hz
V2 = -0.5 volt 40Hz
Vcm = 5 volt 150Hz
R1 = 1k
R2 = 10k
R3 = 1k
R4 = 10K
Si ha quindi che:
R1/R2 = R3/R4 = 1/10
Ad = -10
A.C. Neve – Amplificatore differenziale
2
Come si può notare, sul segnale di uscita non vi è alcuna traccia del segnale Vcm a 150 Hz e, la
tensione differenziale di ingresso è amplificata di un fattore 10.
Modificando invece il solo valore di R4 si ha che:
R4 = 8K
R1/R2 =1/10 mentre R3/R4 = 1/8 per cui Ac è diverso da zero e si ottiene:
Come si può notare, l’uscita non è più sinusoidale a 40 Hz ma è modificata dall’effetto della
componente di rumore a 150 Hz.
A.C. Neve – Amplificatore differenziale
3
Il circuito fin ora esaminato presenta però alcuni svantaggi da non sottovalutare:
•
•
•
•
Ha una bassa impedenza di ingresso
L’offset totale risulta proporzionale ai valori resistivi
Trovare coppie di resistenze uguali e con lo stesso coefficiente di temperatura (matched)
Problematica variazione del guadagno Ad.
Nella figura seguente viene proposto un circuito alternativo a quello ora esaminato detto
Instrumentational Amplifier (Amplificatore per Strumentazione) il quale offre delle prestazioni
notevolmente superiori e limitando gli svantaggi prima esposti.
Lo stadio finale è costituito dal classico amplificatore differenziale con guadagno unitario in quanto,
le quattro resistenze Ro sono tutte uguali e quindi meno problematiche da implementare.
I primi due stadi sono invece degli amplificatori in configurazione non invertente i quali offrono
una impedenza di ingresso estremamente elevata specialmente se con ingressi a FET.
Osservando il circuito si nota che:
Vo1 = − R1 ⋅ I + V 1 + Vcm
con
Vo2 = + R 2 ⋅ I + V 2 + Vcm
I=
V 2 − V1
R
Sostituendo il valore di I nelle equazioni di Vo1 e Vo2, si ha che:
A.C. Neve – Amplificatore differenziale
4
Vo1 = − R1 ⋅
V 2 − V1
+ V 1 + Vcm
R
Vo 2 = + R 2 ⋅
V 2 − V1
+ V 2 + Vcm
R
Sottraendo la prima dalla seconda si ottiene:
R1 + R 2
R1 R 2
Vo 2 − Vo1 = (V 2 − V 1) + (V 2 − V 1) ⋅ +
= (V 2 − V 1) ⋅ 1 +
R
R
R
come si può notare, il contributo della tensione di modo comune è nullo cioè Ac = 0.
Osservando che il termine Vo2-Vo1 rappresenta la tensione differenziale di ingresso dello stadio
finale e che quest’ultimo ha guadagno unitario, si ha che:
R1 + R 2
Vout = (V 2 − V 1) ⋅ 1 +
R
In questo circuito, il valore dell’amplificazione differenziale può essere più comodamente variato
agendo sul solo valore di R.
Con i valori indicati nel circuito e con:
V1 = 0.5 volt 40Hz, V2 = 0.5 volt 40Hz, Vcm = 5 volt 150Hz ed Ad = 4, si ottiene che:
A.C. Neve – Amplificatore differenziale
5
Una ulteriore evoluzione dell’amplificatore differenziale è proposta nel circuito seguente:
Questo circuito, oltre ad offrire i vantaggi del circuito precedente, consente un controllo lineare del
guadagno infatti:
R5
Vout = −(V 2 − V 1) ⋅
R6
è quindi possibile modificate il valore del guadagno agendo sul solo valore di R5.
A.C. Neve – Amplificatore differenziale
6