Moto di puro rotolamento
Definizione: quando un corpo rotola senza strisciare, ovvero la velocità
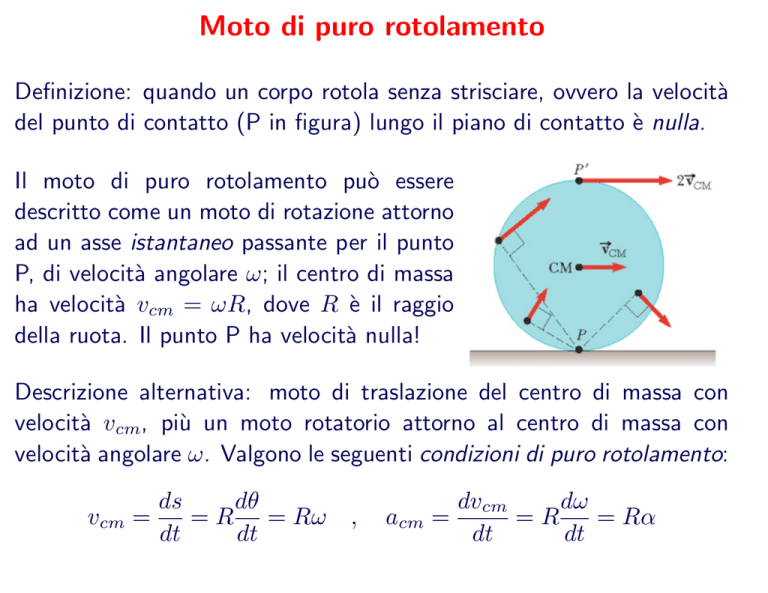
del punto di contatto (P in figura) lungo il piano di contatto è nulla.
Il moto di puro rotolamento può essere
descritto come un moto di rotazione attorno
ad un asse istantaneo passante per il punto
P, di velocità angolare ω; il centro di massa
ha velocità vcm = ωR, dove R è il raggio
della ruota. Il punto P ha velocità nulla!
Descrizione alternativa: moto di traslazione del centro di massa con
velocità vcm, più un moto rotatorio attorno al centro di massa con
velocità angolare ω. Valgono le seguenti condizioni di puro rotolamento:
ds
dθ
vcm =
= R = Rω
dt
dt
,
dvcm
dω
acm =
=R
= Rα
dt
dt
Attrito nel moto di puro rotolamento
In verde la traiettoria del centro di massa (che è anche il centro della
ruota), in rosso la traiettoria del punto P (nota come cicloide):
x = R sin(ωt) + ωRt
y = R cos(ωt) + R
Il moto di rotolamento puro può richiedere la presenza di attrito!
Tuttavia l’attrito non fa lavoro: dW = F~a · d~r = 0 perché il punto P di
contatto è fermo. Per lo stesso motivo, l’attrito è presente solo come
attrito statico (l’attrito dinamico è presente solo se il corpo striscia)
Esempio: Energia cinetica di un corpo che rotola
Corpo rigido di massa M , velocità del centro di massa v, momento
d’inerzia I per rotazioni attorno al centro di massa, velocità angolare ω.
Energia cinetica totale:
1
1 2
2
K = M v + Iω
2
2
Esempio: sfera (o cilindro) che rotola
giù per un piano inclinato. Avremo:
v2
2
I
R2
v = ωR (condizione di puro rotolamento), K =
M+
.
Per la conservazione dell’energia meccanica,
v2
I
Ui = M g(h + R) = 2 M + R2 + M gR = Kf + Uf
q
q
gh
10gh
2
da cui v = M2M
.
Per
una
sfera:
I
=
2M
R
/5,
v
=
7 .
+I/R2
Notare che v <
√
2gh, velocità finale senza rotolamento, per qualunque I. Perché?
Esempio: Dinamica di un corpo che rotola
Risolviamo ora lo stesso problema con forze e momenti.
• Lungo il piano: M a = M g sin θ − Fa, dove Fa è la forza di attrito
• Ortogonale al piano: N = M g cos θ, dove N è la reazione vincolare
• Rispetto al centro della sfera: Iα = τ = RFa, dove α = a/R.
Sostituendo dall’ultima equazione Fa = Ia/R2 nella prima, si ottiene
(M + I/R2)a = M g sin θ da cui:
M g sin θ
a=
,
2
M + I/R
per una sfera:
5
a = g sin θ
7
ovvero un moto uniformemente accelerato, che può essere facilmente
risolto e dà lo stesso risultato del calcolo precedente.
Esempio: Forze in un corpo che rotola
Notare che
• l’attrito entra nelle equazioni del moto anche se non fa lavoro
IF
• la forza di attrito vale Fa = M R
2 +I , dove F = M g sin θ è forza che
spinge il corpo, ed è opposta a questa
• deve valere la condizione Fa ≤ µsN = µsM g cos θ o altrimenti il
corpo inizia a scivolare!
Risolviamo ora il problema come moto di rotazione attorno ad un asse
passante per il punto di contatto istantaneo. L’equazione del moto è
I 0α = τ = RM g sin θ
dove
I 0 = I + M R2
(teorema degli assi paralleli) da cui si ritrova il risultato precedente.
Notare come la soluzione sia più semplice e l’attrito non compaia più.
Esempio: Moto causato da momento torcente
Nel caso precedente, una forza esterna
applicata al corpo causa il rotolamento. In
altri casi (esempio: ruota di automobile) un
momento torcente causa il moto di rotazione
Dalle equazioni Iα = τ − RFa e M a = Fa e dalla condizione a = αR
di puro rotolamento otteniamo a =
Rτ
,
I+M R2
Fa =
M Rτ
.
I+M R2
Da notare che è la forza di attrito che spinge la ruota in avanti!
A parità di accelerazione, la forza di attrito è maggiore se il corpo è
spinto da una forza esterna o da un momento torcente?
per rispondere, servono i risultati ottenuti per il corpo che rotola da un piano inclinato:
a=
F R2
,
I+M R2
Fa =
IF
,
I+M R2
dove F è la forza che spinge il corpo.












