Rotolamento
Energia di un corpo rotolante
Esempi Il Rotolamento: moto rototraslazionale
Quando una ruota
si muove senza
slittamenti siamo
in presenza di un
rotolamento.
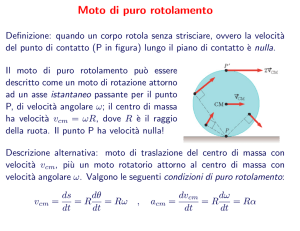
In un intervallo di tempo dt il centro della ruota, o, si muove in avanti
con velocità vcm, mentre il punto p descrive una curva nota come
cicloide.
Tale curva è la combinazione del moto lineare del mozzo della ruota
rispetto al suolo, più il moto circolare che un punto periferico fa
attorno al mozzo
vcm = ω R
moto del rotolamento
Rotolamento puro
§ Il moto di rotolamento può
essere descritto anche come
un moto puramente
rotazionale, immaginando
che tutta la ruota giri attorno
al punto di contatto.
§ Contatto che risulta diverso
istante per istante.
§ Anche con questo modello
si vede che la velocità
tangenziale del punto T vale
il doppio della velocità
dell’asse centrale
vT = ω (2r) = 2ωr = 2vcm
Energia cinetica del Rotolamento
Supponiamo di avere un puro
rotolamento ed usiamo il modello della
rotazione attorno al punto di contatto
con il suolo.
Ek = ½ IP ω2
Dove il momento di inerzia è calcolato
rispetto a P e vale IP = Icm + MR2, così
che l’Energia cinetica è:
Ek = ½ (Icm + MR2)ω2
ovvero
Ek = ½ Icm ω2 + ½ Mv2cm
L’energia cinetica di un oggetto rotolante è data dalla somma di Ek
rotazionale attorno al suo c.m. più l’energia cinetica Ek lineare del c.m.
Piano inclinato e rotolamento
Il moto del corpo riportato in figura si
descrive partendo dalla 2a legge di
Newton.
ΣF = Ma
e per i moti angolari Στ = Iα.
Per i moti lineari
fs - Fg sinθ = M acm
(per fs si sa solo che si oppone allo
scivolamento, non si può supporre una fs,max)
R fs = Icm α (fra le due equazion si hanno
tre incognite).
La terza relazione è: -acm = αR
(facendo attenzione ai segni)
Accelerazione di puro rotolamento
La soluzione è un po’ faticosa, ma comprensibile
f s − Mg sin θ = Macm Si ricavi α dalla terza equazione e la si
Rf s = I cmα
Rα = −acm
avremo
sostituisce nella seconda
f s = Mg sin θ + Macm
I cm acm
fs =
(−
)
R
R
I cm
a
2 cm
R
I
I
Mg sin θ = − Macm − cm2 acm = −acm ( M + cm2 )
R
R
I
g sin θ = −acm (1 + cm 2 )
MR
sin θ
acm =
g
2
1 + I cm MR
Ianello= MR2
Mg sin θ + Macm = −
Isfera= 2/5 MR2
Icilindro = ½ MR2
θ =30°
Esempio di rotolamento
Trovare il rapporto fra la velocità raggiunta da una ruota che rotola e la
stessa ruota che scivoli senza attrito lungo un piano inclinato
1
1
2
I 0ω 2 + Mv0
2
2
v
1
I 0 = MR 2 ω = 0
h = l sin 30
2
R
Mgh =
2
1 ⎛ 1
⎞⎛ v ⎞ 1
Mgh = ⎜ MR 2 ⎟⎜ 0 ⎟ + Mv02
2 ⎝ 2
⎠⎝ R ⎠ 2
gh =
h
11 2 1 2
v0 + v0
22
2
3 2
4
4
2
gh = v0 → v0 = gh → v0 =
gh
4
3
3
v0
=
v
1
Mv 2
2
v 2 = 2 gh → v = 2 gh
Mgh =
1
1
4
2
⋅
2
gh
2
2
3
3 = 1,73 =
=
=
= 0,82
1,41
1,41 ⋅ 1,73 2,44
2 gh
2
…e se fosse stata una boccia?
…occhio al momento di inerzia I0
1
1
2
I 0ω 2 + Mv0
2
2
2
v
I 0 = MR 2 ω = 0
h = l sin 30
5
R
Mgh =
h
2
1 ⎛ 2
⎞⎛ v ⎞ 1
2
Mgh = ⎜ MR 2 ⎟⎜ 0 ⎟ + Mv0
2 ⎝ 5
⎠⎝ R ⎠ 2
7 2
10
10
2
gh = v0 → v0 = gh → v0 =
gh
10
7
7
1
Mv 2
2
v 2 = 2 gh → v = 2 gh
Mgh =
10
10
gh
v0
1,19
= 7
= 7 =
= 0,84
v
2 gh
2 1,41