3. Limite finito per x che tende all’infinito
Un altro comportamento delle la funzioni che può essere espresso con rigore tramite una operazione
matematica, è quello della stabilizzazione attorno ad un valore finito ℓ quando la variabile indipendente x
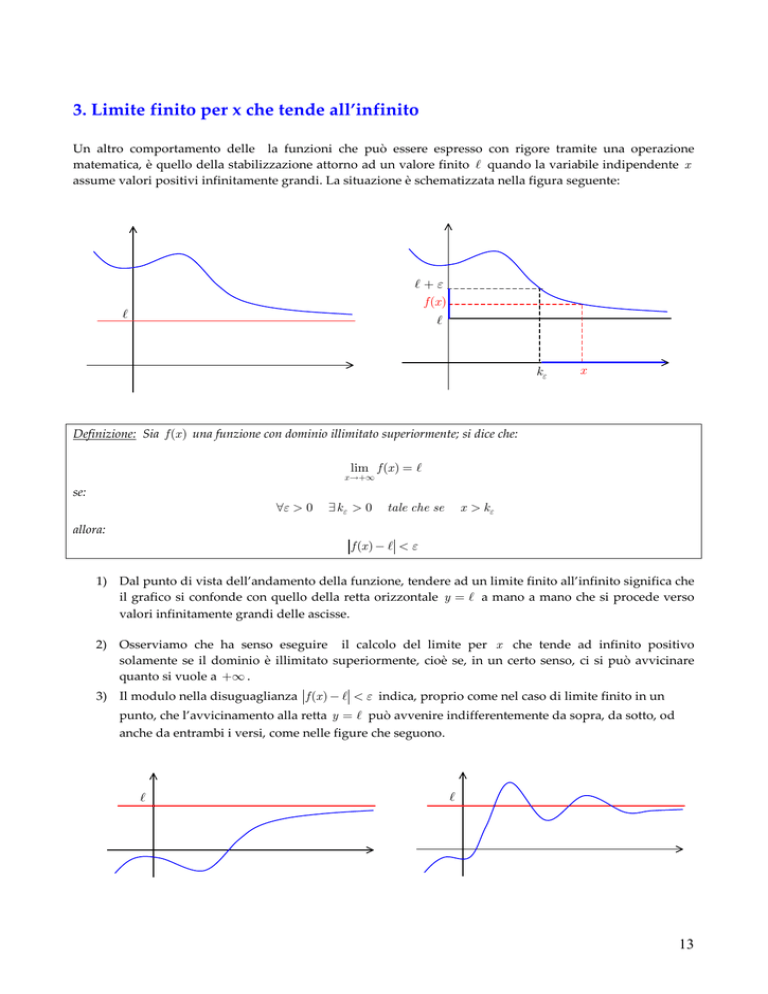
assume valori positivi infinitamente grandi. La situazione è schematizzata nella figura seguente:
ℓ+ε
f (x )
ℓ
ℓ
kε
x
Definizione: Sia f (x ) una funzione con dominio illimitato superiormente; si dice che:
lim f (x ) = ℓ
x →+∞
se:
∀ε > 0
∃ kε > 0
x > kε
tale che se
allora:
f (x ) − ℓ < ε
1) Dal punto di vista dell’andamento della funzione, tendere ad un limite finito all’infinito significa che
il grafico si confonde con quello della retta orizzontale y = ℓ a mano a mano che si procede verso
valori infinitamente grandi delle ascisse.
2) Osserviamo che ha senso eseguire il calcolo del limite per x che tende ad infinito positivo
solamente se il dominio è illimitato superiormente, cioè se, in un certo senso, ci si può avvicinare
quanto si vuole a +∞ .
3) Il modulo nella disuguaglianza f (x ) − ℓ < ε indica, proprio come nel caso di limite finito in un
punto, che l’avvicinamento alla retta y = ℓ può avvenire indifferentemente da sopra, da sotto, od
anche da entrambi i versi, come nelle figure che seguono.
ℓ
ℓ
13
In maniera analoga si può definire rigorosamente il comportamento di una funzione che si approssima ad un
valore ℓ quando la x tende verso valori infinitamente negativi.
Definizione:
Sia f (x ) una funzione con dominio illimitato
inferiormente; si dice che:
lim f (x ) = ℓ
ℓ
f (x )
x →−∞
se:
∀ε > 0
∃ kε > 0
x < −k ε
tale che se
ℓ−ε
allora:
x
−kε
f (x ) − ℓ < ε
Esempio 1
Verificare il limite:
3x − 1
3
=
x →+∞ 2x + 3
2
lim
Si tratta di provare che la disuguaglianza:
3x − 1 3
− <ε
2x + 3 2
è soddisfatta in un intorno di +∞ , cioè in un insieme della forma (k ε ; +∞) . Risolviamo:
−ε <
3x − 1 3
− <ε
2x + 3 2
⇒
−ε <
−11
<ε
4x + 6
Si perviene al sistema:
−11
−ε < 0
4x + 6
−11
+ε> 0
4x + 6
⇒
−4εx − 6ε − 11
<0
4x + 6
4εx + 6ε − 11
>0
4x + 6
Risolviamo la prima disequazione facendo il prodotto del segno del numeratore per quello del
denominatore:
−4εx − 6ε − 11
<0
4x + 6
−4εx − 6ε − 11 > 0
⇒
4x + 6 > 0
⇒
⇒
3
x >−
2
−6ε − 11
x<
4ε
3 11
− −
2 4ε
−32
segno di:
−
−4εx − 6ε − 11
−
−
−
+
4x + 6
−
+
−
+
14
−
−
−
3 11
+
2 4ε
+
+
+
+
−
+
Analogamente risolviamo la seconda:
4εx + 6ε − 11
>0
4x + 6
−32
3 11
4εx + 6ε − 11 > 0 ⇒ x > − +
2 4ε
⇒
3
4x + 6 > 0 ⇒ x > −
2
−
segno di:
4εx + 6ε − 11
4x + 6
Prendiamo l’intersezione delle due soluzioni:
3 11
− −
2 4ε
−32
−
3 11
+
2 4ε
− 4 εx − 6 ε − 1 1
< 0
4x + 6
4 εx + 6 ε − 1 1
> 0
4x + 6
Il limite è senz’altro verificato in quanto la soluzione complessiva comprende al suo interno un intorno di
3 11
(od un valore
infinito positivo, cioè un insieme della forma (k ε ; +∞) , dove in questo caso è k ε = − +
2 4ε
positivo più grande di esso se per qualche ε viene k ε < 0 ).
Nel particolare caso proposto, il grafico della
funzione è noto, si tratta di una funzione
omografica, la cui forma generica è:
f (x ) =
ax + b
cx + d
Ora, voi non ci crederete, ma abbiamo
studiato in terza questa classe di funzioni,
imparando che esse hanno un asintoto
d
ed un asintoto
verticale in x = −
c
a
orizzontale di equazione y = . Nel presente
c
3
3
caso si ha x = − 2 ed y = 2 . Trovando le
3
3
2
f (x )
2−ε
x
−32
A
intersezioni con gli assi A(0; − 1 3) e B(1 3 ; 0)
è possibile rappresentarla graficamente.
Come del resto si intuisce dal grafico, la nostra verifica ha mostrato pure che
disequazione
3x − 1 3
− <ε
2x + 3 2
B
3
11
2
4ε
kε = − +
lim
x →−∞
3x − 1
3
= . Difatti la
2x + 3
2
è verificata anche in un intorno di −∞ , cioè un insieme della
3 11
.
forma (−∞; −k ε ) , ma stavolta con −k ε = − −
2 4ε
Studiare Tomo C1 pp 45-47, es p326 da 65 a 75 ad libitum.
15