Singolarità e funzioni olomorfe: appunti di analisi complessa

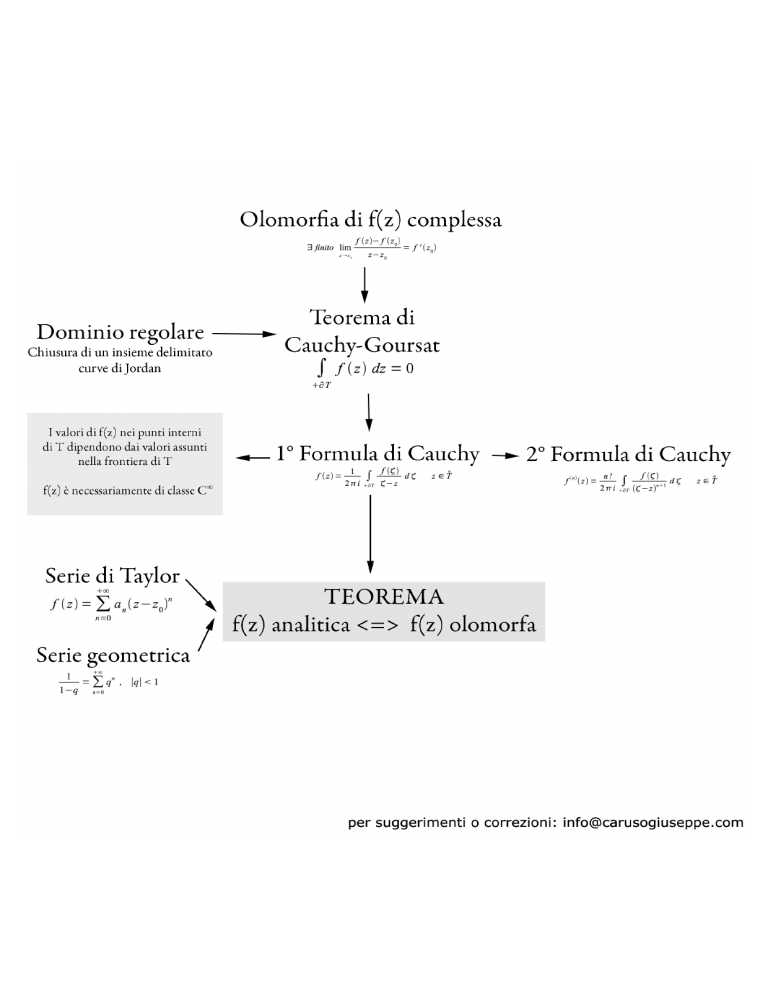
Singolarità e punto all'infinito di una funzione olomorfa in Ω
Per poter classificare le singolarità di una funzione è necessario conoscere i seguenti concetti
Sviluppo in serie di Laurent1 e Teorema di Laurent
Corona circolare
Sia f ( z ) una funzione olomorfa su C R R
Allora esistono e sono unici gli a n ∈ ℂ (n ∈ ℤ) tali che:
1,
Siano 0 ≤ R1 ≤ R2 ≤ +∞
z0 ∈ ℂ , C R
1,
R2
+∞
= { z ∈ ℂ : R1  ∣z − z 0∣  R2 }
f ( z) =
∑
n
n =−∞
definita in tale modo, la corona circolare può
anche essere:
an =
an ( z − z 0) , ∀ z ∈ C R
∫
+γϱ
•
•
Il piano complesso privato di un punto
Il complementare di un cerchio
2
1,
R2
dove
f (ζ)
dζ
( ζ− z 0 )n+1
dove γϱ è la circonferenza di centro z 0 e raggio R1 < ϱ < R2
* in realtà qua è stata considerata una generica curva invece che una circonferenza.
Singolarità
Tipo
Definizione2
<=>
<=>
z0 singolarità
eliminabile3
parte da
n =0
f(z) è convergente per
z → z0
∃ Br  z 0  ⊆  e L  0 :
✴
∣ f  z∣ ≤ L su B r  z 0 
z0 polo di
ordine m
parte da
n=m
(z – z0)m f (z)
è convergente ≠ 0
per z → z0
f(z) diverge per z → z0
z0 singolarità
essenziale
ha infinite
potenze
negative
non esiste lim f  z
z z 0
nè finito nè infinito
Residuo
a−1
✴
Teorema di Picard
  0 , B ✴  z 0 ∩ = A
∃ al più ∈ℂ :
f  A  = ℂ −{} ∀   0
0
lim
z z0
1
D n−1 [ z−z 0n f z ]
n−1!
→ si calcola direttamente tramite lo
sviluppo o l'integrazione
→ si ricava per differenza tramite il
corollario del teorema dei residui
(pag. 101)
Punto all'infinito ∞
Sia  ⊆ ℂ un aperto tale che il complementare di  sia un compatto. ⇒ ∃ R  0 : {z ∈ ℂ: ∣z∣  R} ⊆ 
1
✴
Sia f  z : ℂ , f  z olomorfa. La funzione g  = f   è definita nel disco bucato B 1 0

R
Tipo
Definizione
<=>
<=>
Regolare
Il punto ω = 0
è una singolarità
eliminabile per g(ω)
f(z) è convergente per
z→∞
∣ f  z ∣ ≤ L ∀ ∣z∣  r
Polo di
ordine m
Il punto ω = 0
è polo di ordine m
per g(ω)
f(z) è divergente per
z→∞
Essenziale
Il punto ω = 0
è singolarità essenziale
per g(ω)
non esiste lim f  z 
z ∞
nè finito nè infinito
Residuo
∃ r 0 e L  0 :
∃ m  0 intero :
∣ f  z∣
zm
 l ≠ 0 per z  ∞
-
−a−1
→ con la definizione:
−
1
∫ f  z dz
2  i 
→ oppure tramite
la formula:
Res−
1
1
f  ,0
2


[email protected]
1 Si pronuncia «loran»
2 Definizione basata sullo sviluppo di Laurent
3 Si può anche dire «singolarità fittizia»
Zero di una funzione olomorfa
Sia  ⊆ ℂ un aperto. Sia f  z : ℂ , f  z  olomorfa.
Sia z 0 uno zero della funzione f  z
Tipo
z0 zero di ordine
m
Definizione
Esiste g(z) olomorfa in Ω: f(z0) = f'(z0) = … = f(m-1)(z0) = 0
e
f(z) = (z – z0)m g(z) in Ω
f(m)(z0) ≠ 0
e g(z0) ≠ 0
z0 zero di ordine z0 non è uno zero di ordine
infinito
finito
z0 è punto isolato per Zf
z0 zero isolato
<=>
∃   0 : B  ∩  = z0
(1)
f
n 
Legame con il polo
⇒ z 0 polo di ordine m per
 z0 = 0 ∀ n ∈ ℕ
z0 zero di ordine finito m
<=>
z0 zero isolato
1
f z
⇒ z 0 singolarità essenziale
1
per
f z
⇒ z 0 polo di qualche ordine m
1
per
f z
Nozione di zero di una funzione olomorfa

Principio d ' identità delle funzioni olomorfe
Sia  ⊆ ℂ un aperto connesso.Siano f  z , g  z due funzioni olomorfe su 
Se l ' insieme dei punti in cui le funzioni coincidono ha un puntodi accumulazione z 0 ∈ 
allora
f  z  = g z  in 
Si noti che il teorema è falso per le funzioni reali
[email protected]
1 Zf è l'insieme degli zeri della funzione f(z)